Sommaire
Nuage de points. Point moyen.
Série statistique à deux variables
Dans une population, on étudie deux caractères quantitatifs x et y.
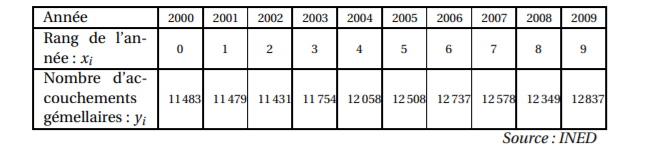
Dans cet exemple, les deux séries sont : le rang de l’année et le nombre de naissances de jumeaux comme dans le tableau ci-dessous.
Définition:
Dans un repère, le nuage de points associé à la série statistique est l’ensemble des points de coordonnées (x_i;y_i).
Par exemple les points (0;11483) , (1;11479483) , (2;11431) , …
Le point moyen de ce nuage est le point G de coordonnées \bar x et \bar y où \bar x est la moyenne des x_i et \bar y est la moyenne des y_i.
Exercice n°1 : voici la série à deux variables :

- Représenter dans un repère le nuage de points.
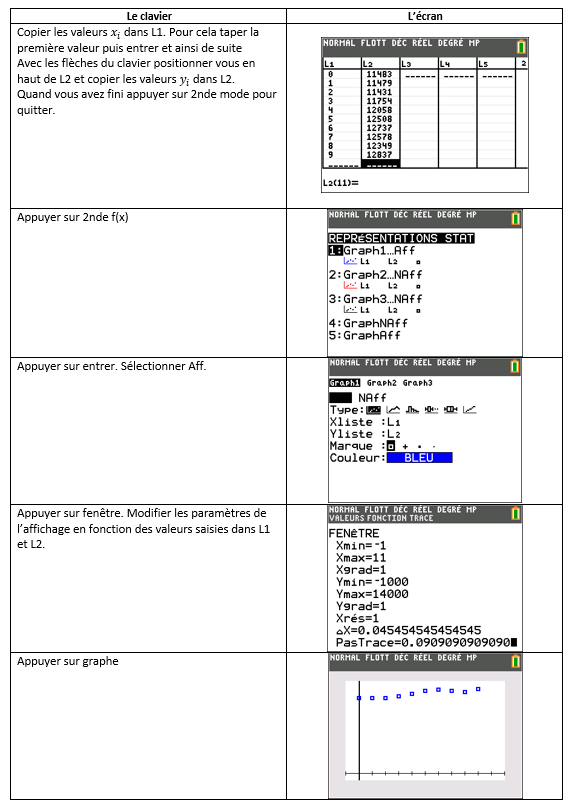
a. A l’aide de la TI 83 Premium CE.
b. A l’aide de Géogébra.
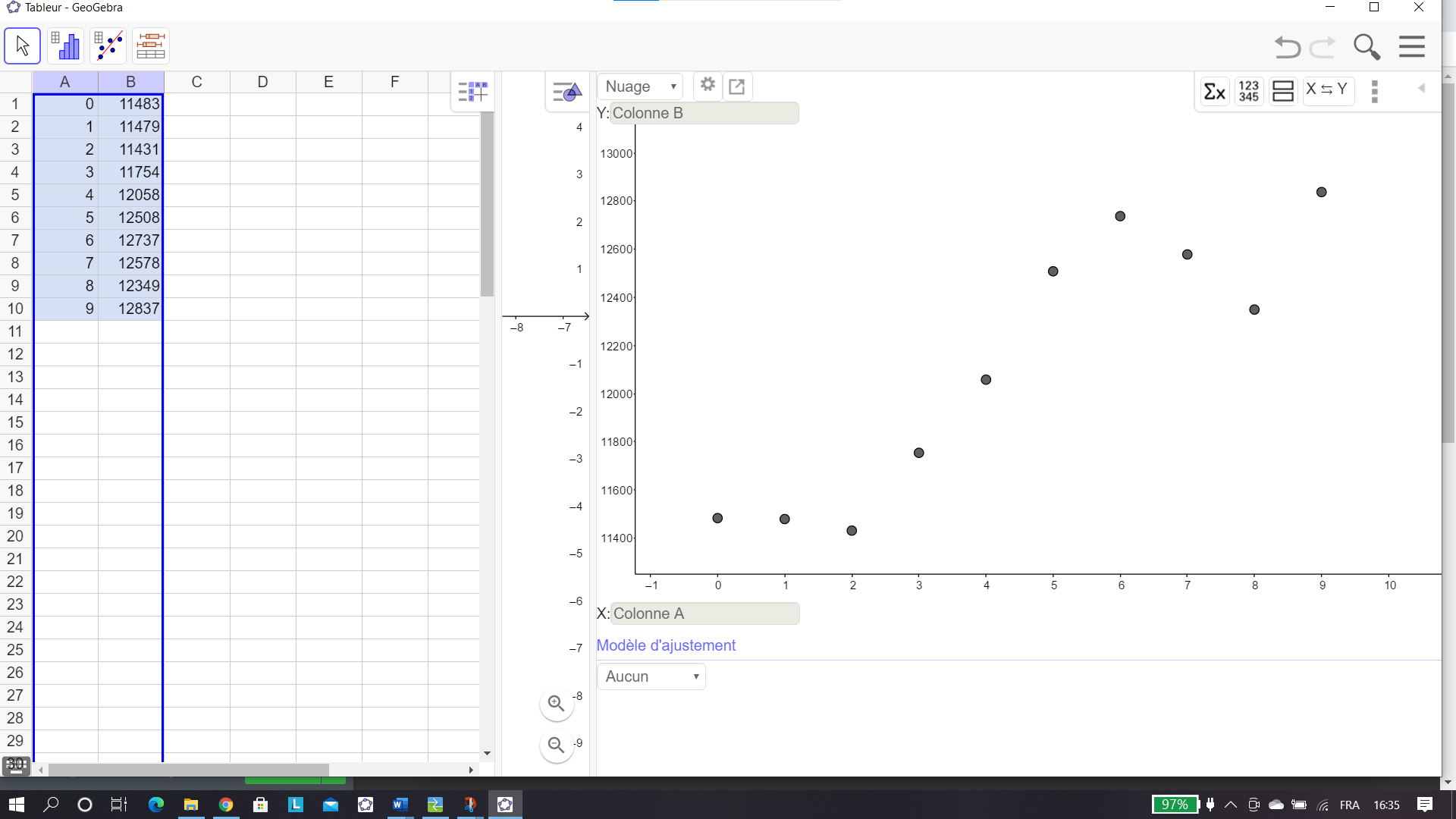
Lors de l’ouverture de la fenêtre Géogébra, cliquer à droite sur Tableur.
Saisir les valeurs de x dans la colonne A et les valeurs de y dans la colonne B.
On sélectionne les deux colonnes A et B.
On clique sur le deuxième onglet en haut à partir de la gauche.On clique dans le menu déroulant sur statistiques à deux variables.
Le graphique apparaît à droite.
2. Déterminer les coordonnées du point moyen noté G.
a. A l’aide de la TI 83 Premium CE.
b. A l’aide de Géogébra.
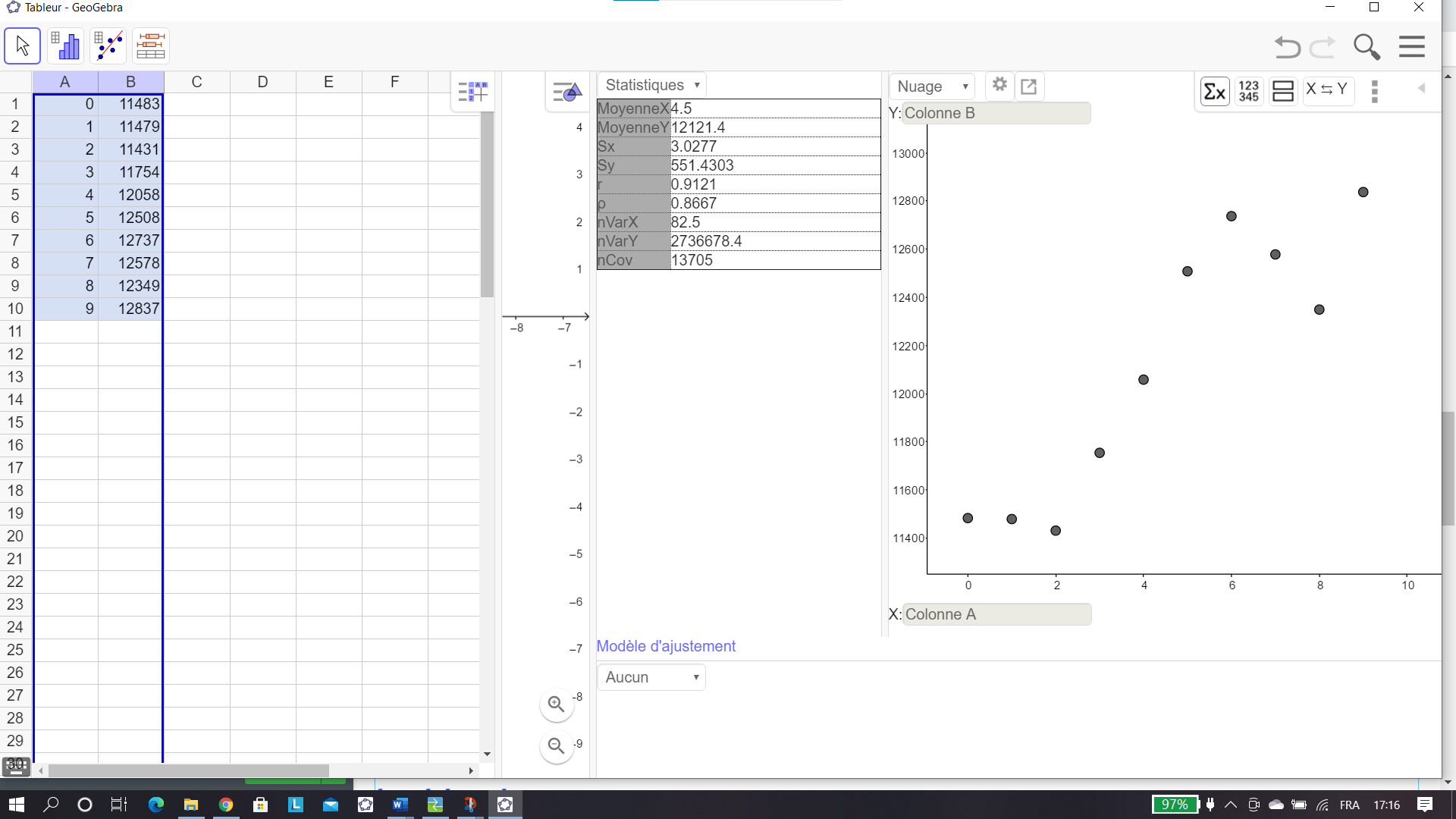
On a déjà obtenu la représentation graphique à la question 1.b.
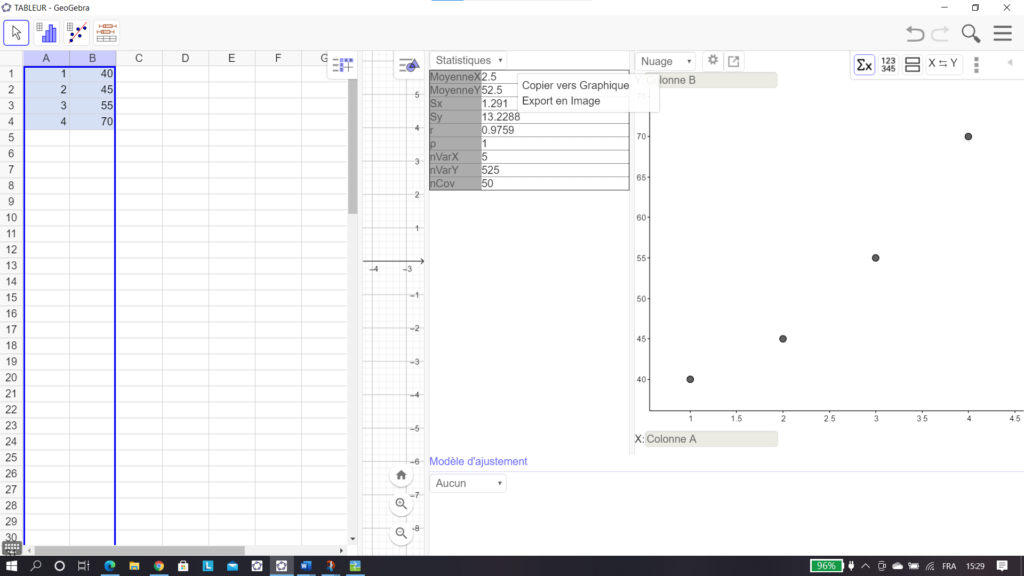
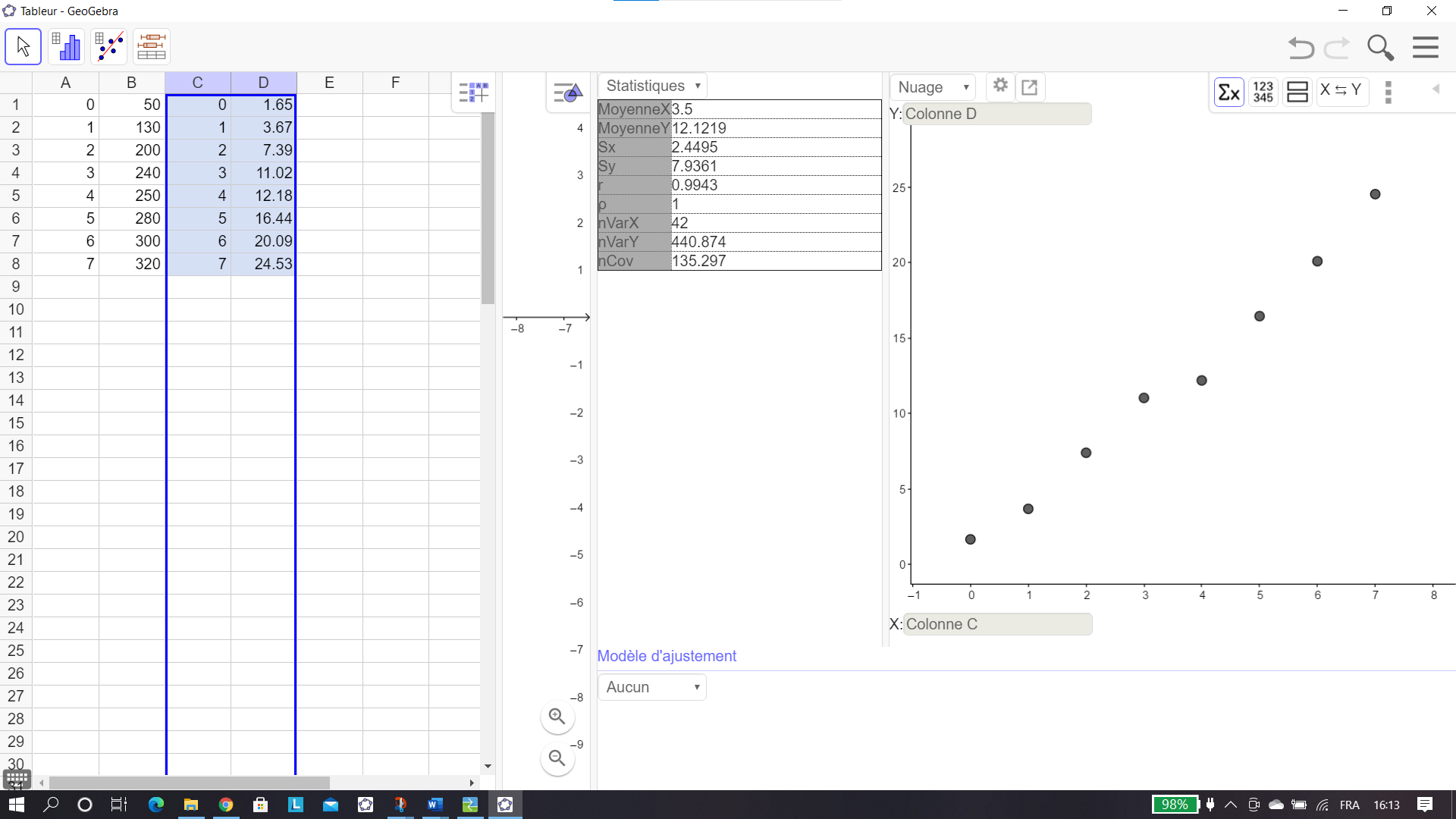
On clique sur le premier onglet en haut à droite de l’écran symbolisé par \Sigma X .Au milieu apparaît une colonne Statistiques. Les coordonnées de G sont les deux premières moyennes.
Exercice n°2 : Le tableau ci-dessous donne le nombre de pages visitées, exprimé en milliers, durant chacune des
quatre semaines suivant l’ouverture d’un site internet.

- Représenter dans un repère le nuage de points.
a. A l’aide de la TI 83 Premium CE.
b. A l’aide de Géogébra.
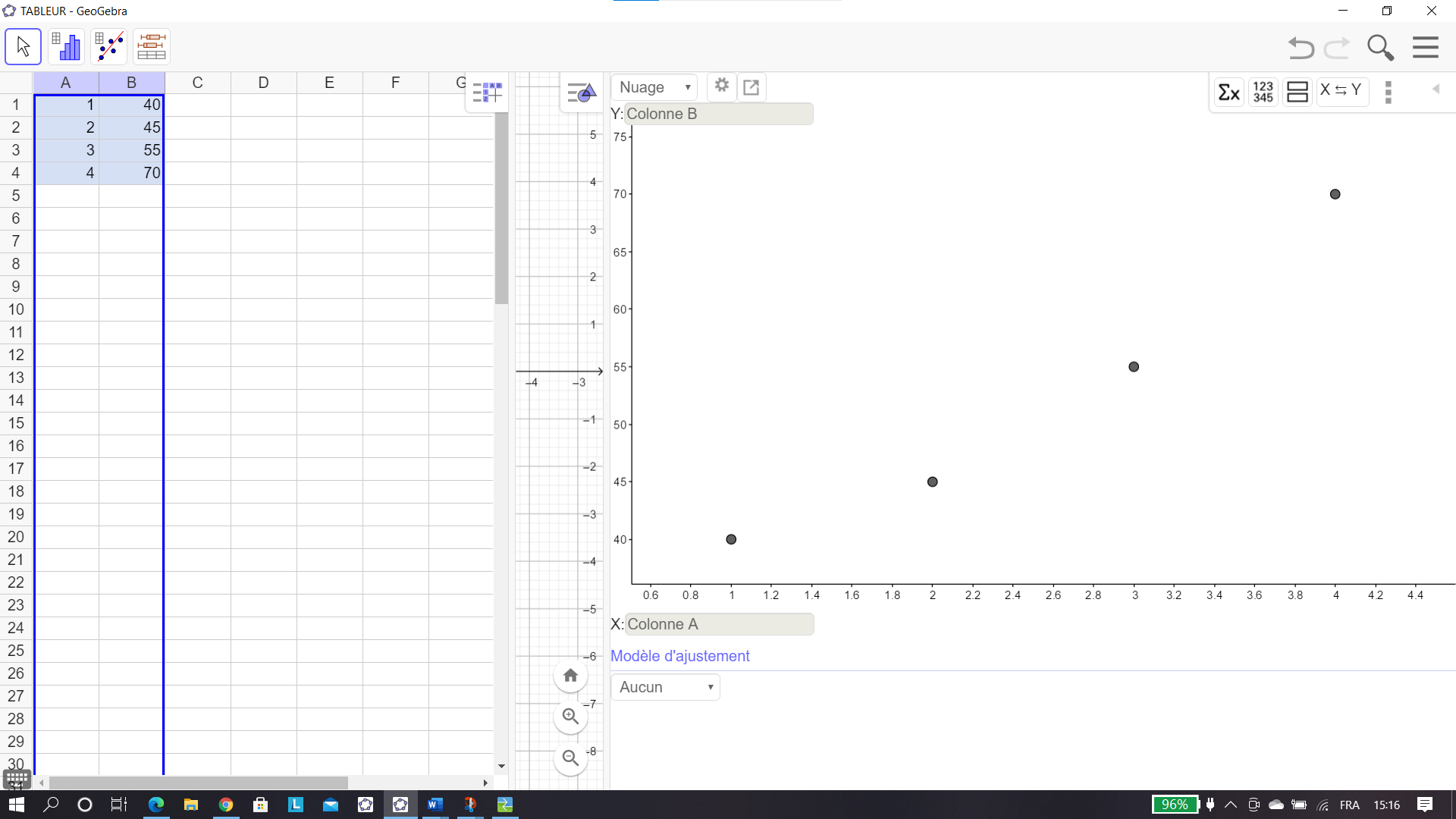
Lors de l’ouverture de la fenêtre Géogébra, cliquer à droite sur Tableur.
Saisir les valeurs de x dans la colonne A et les valeurs de y dans la colonne B.
On sélectionne les deux colonnes A et B.
On clique sur le deuxième onglet en haut à partir de la gauche.On clique dans le menu déroulant sur statistiques à deux variables.
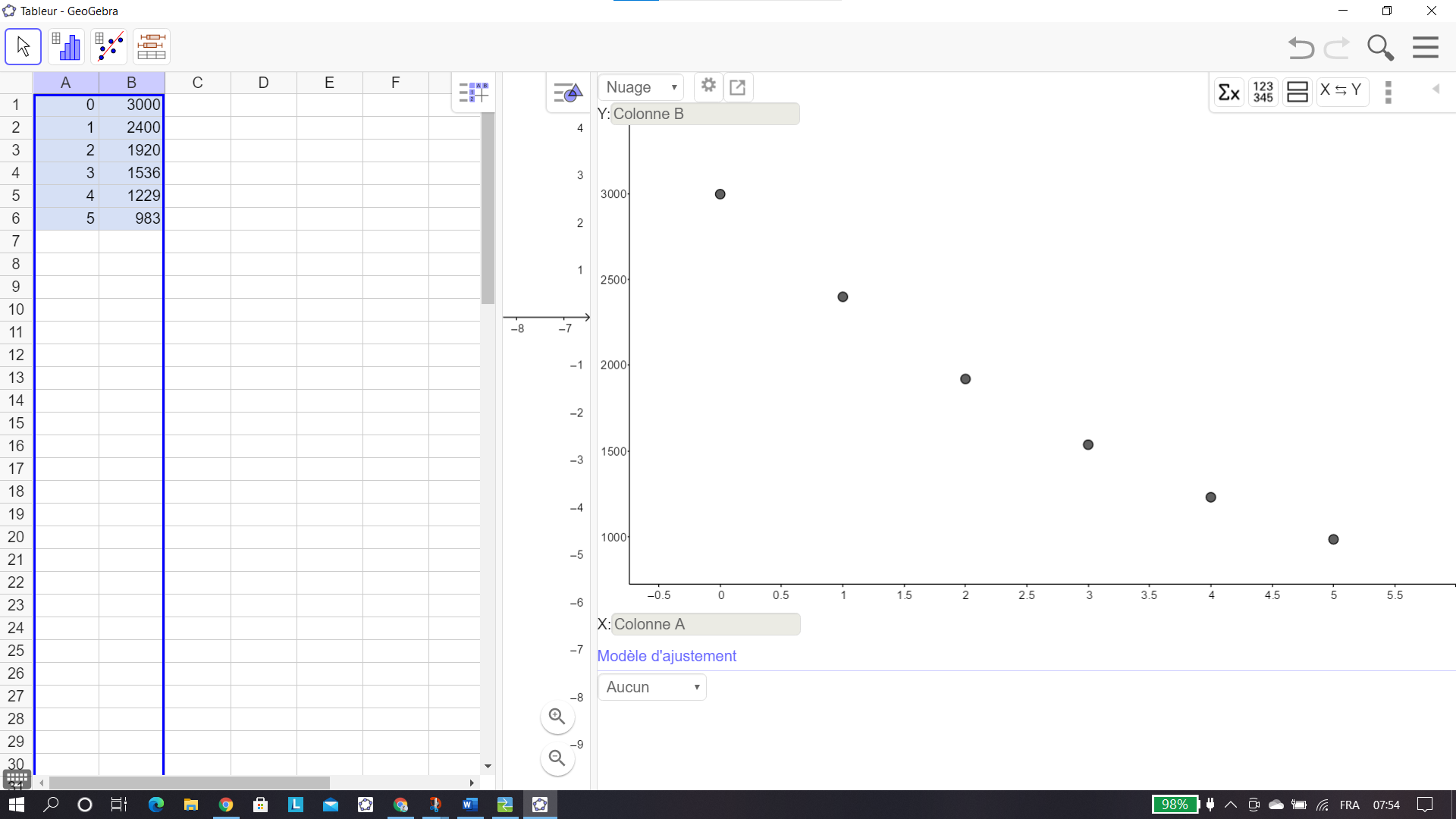
Le graphique apparaît à droite.
2. Déterminer les coordonnées du point moyen noté G.
a. A l’aide de la TI 83 Premium CE.
b. A l’aide de Géogébra.
On a déjà obtenu la représentation graphique à la question 1.b.
On clique sur le premier onglet en haut à droite de l’écran symbolisé par \Sigma X .Au milieu apparaît une colonne Statistiques. Les coordonnées de G sont les deux premières moyennes.
Ajustement affine d’un nuage de points.
Droite d’ajustement affine.Droite des moindres carrés.
Définition :
Lorsque les points d’un nuage sont sensiblement alignés, réaliser un ajustement affine revient à tracer une droite qui passe au plus près des points du nuage.
Propriété :
La droite des moindres carrés a pour équation y=ax+b avec a=\frac{cov(x,y)}{var(x)} et b=\bar y-a\bar x.
Pour calculer cov(x,y) qui est la covariance des séries statistiques x et y, on applique la formule suivante :
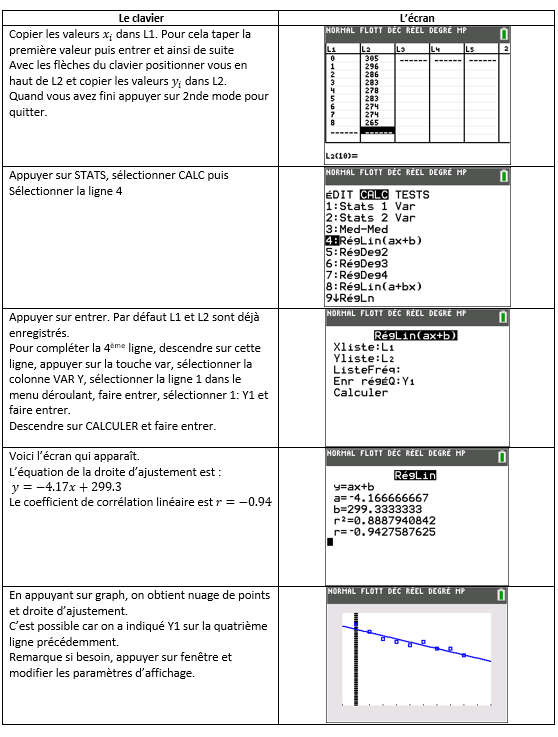
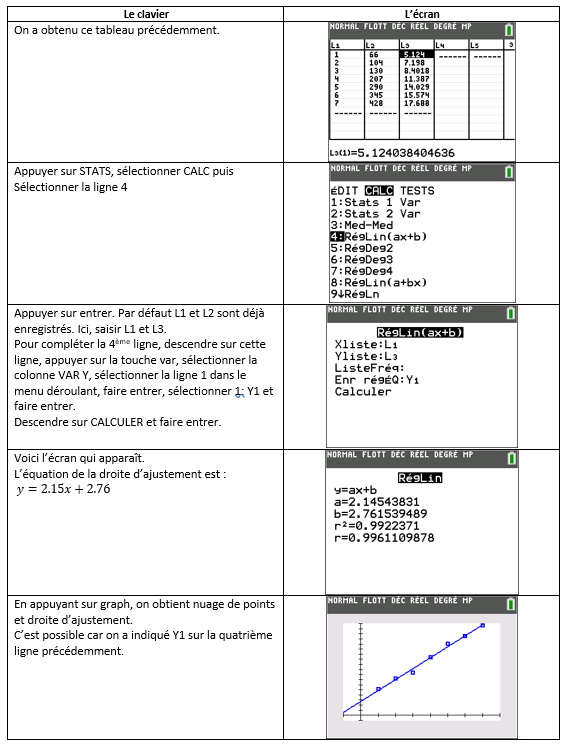
cov(x,y)=\frac{(x_1-\bar x)(y_1-\bar y)+(x_2-\bar x)(y_2-\bar y)+…+(x_n-\bar x)(y_n-\bar y)}{n}On reprend l’exercice n°1 avec les naissances de jumeaux. On va déterminer l’équation de la droite des moindres carrés avec la calculatrice TI-83 Premium :

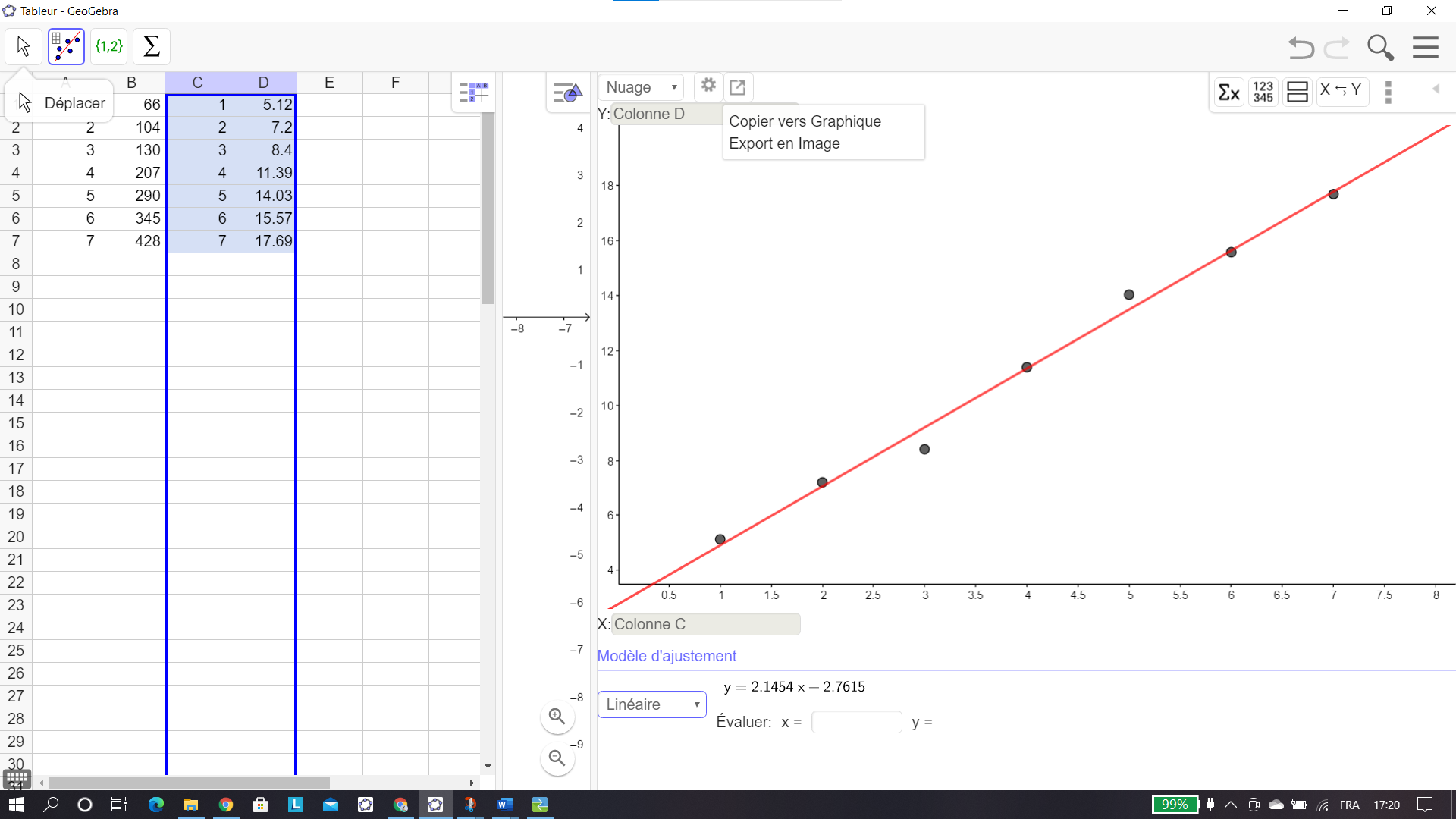
On reprend l’exercice n°1 avec les naissances de jumeaux. On va déterminer l’équation de la droite des moindres carrés avec Géogébra.
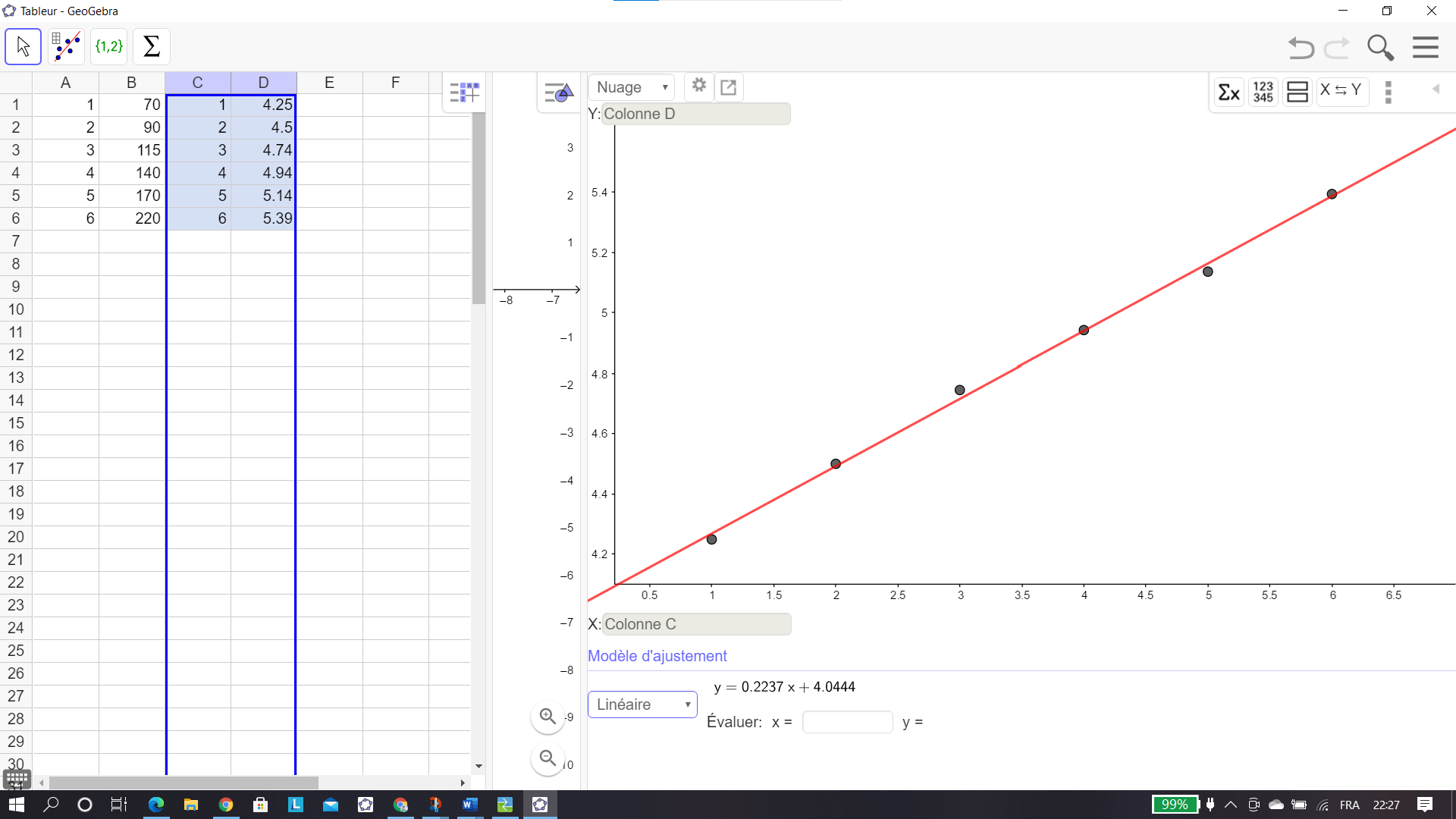
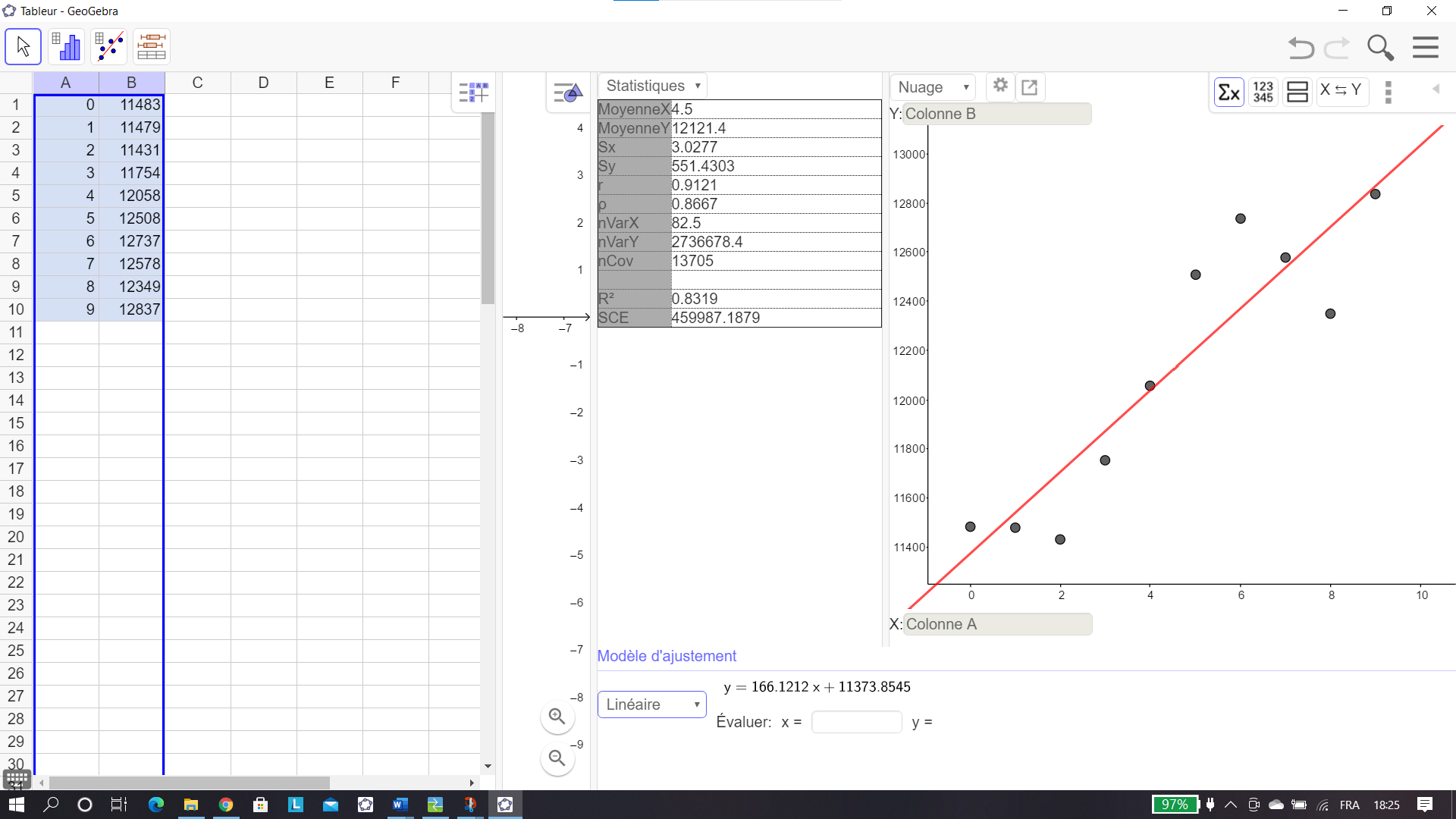
On reprend où on en était arrivés à l’exercice 1 question 2.b.
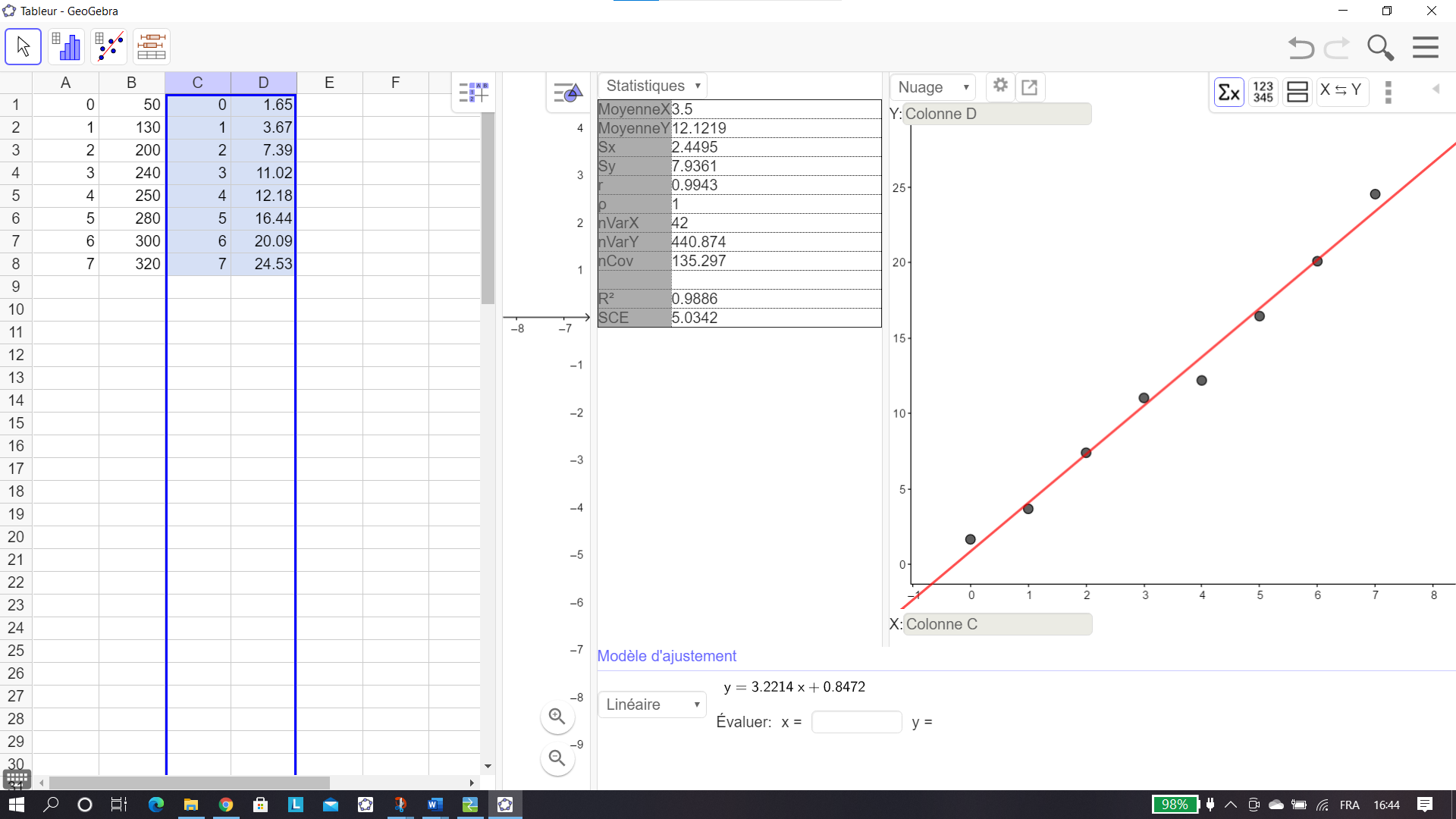
En bas de l’écran, sous Modèle d’ajustement, il y a un cadre. Cliquer sur le petit triangle et sélectionner Linéaire dans le menu déroulant.
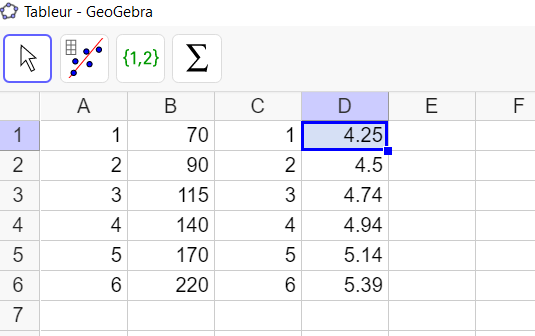
Exercice n°3 : Une machine est achetée 3000 euros.
Le prix de revente y, exprimé en euros, est donné en fonction du nombre x d’années d’utilisation par
le tableau suivant :

- Représenter dans un repère le nuage de points.
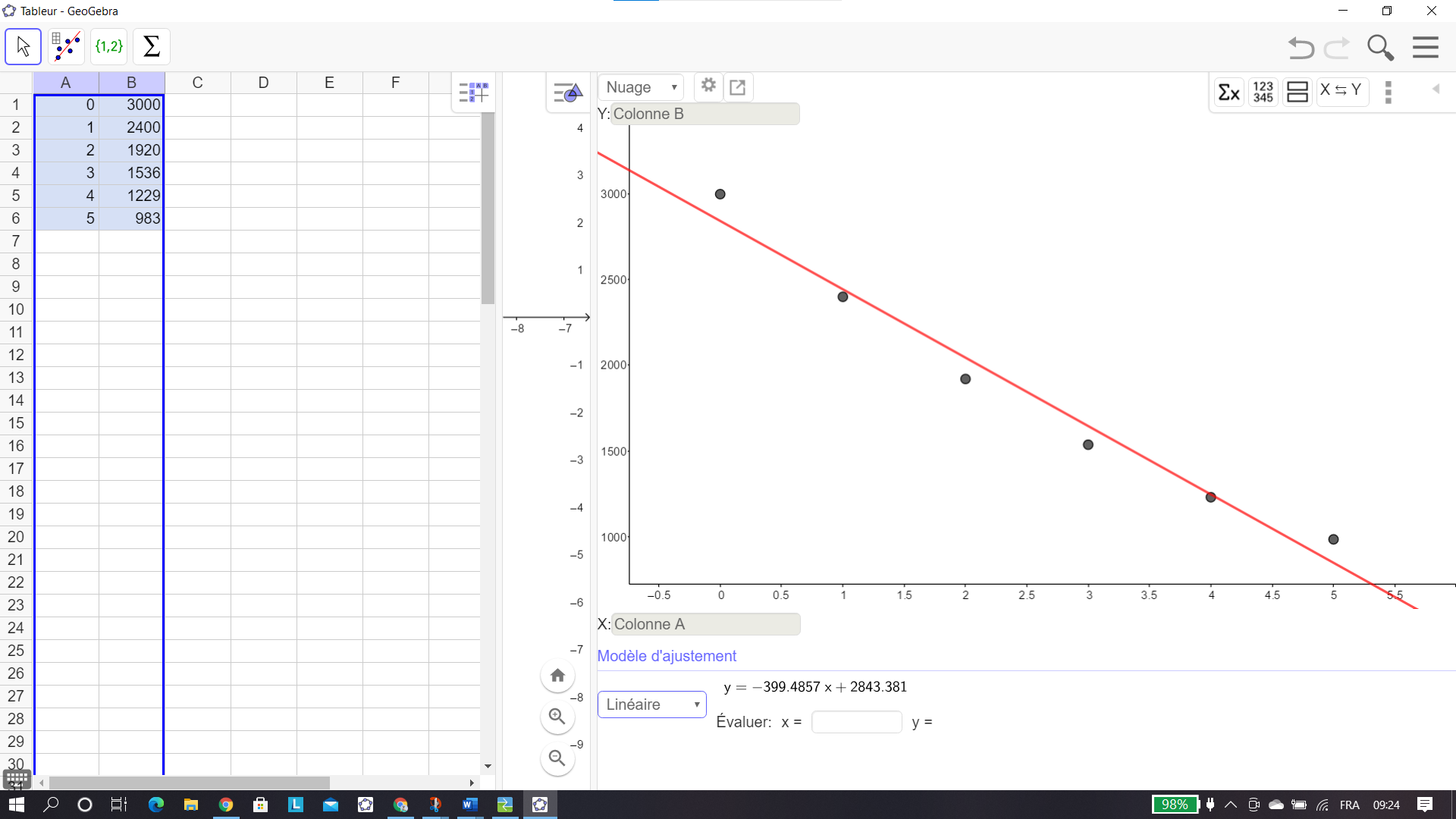
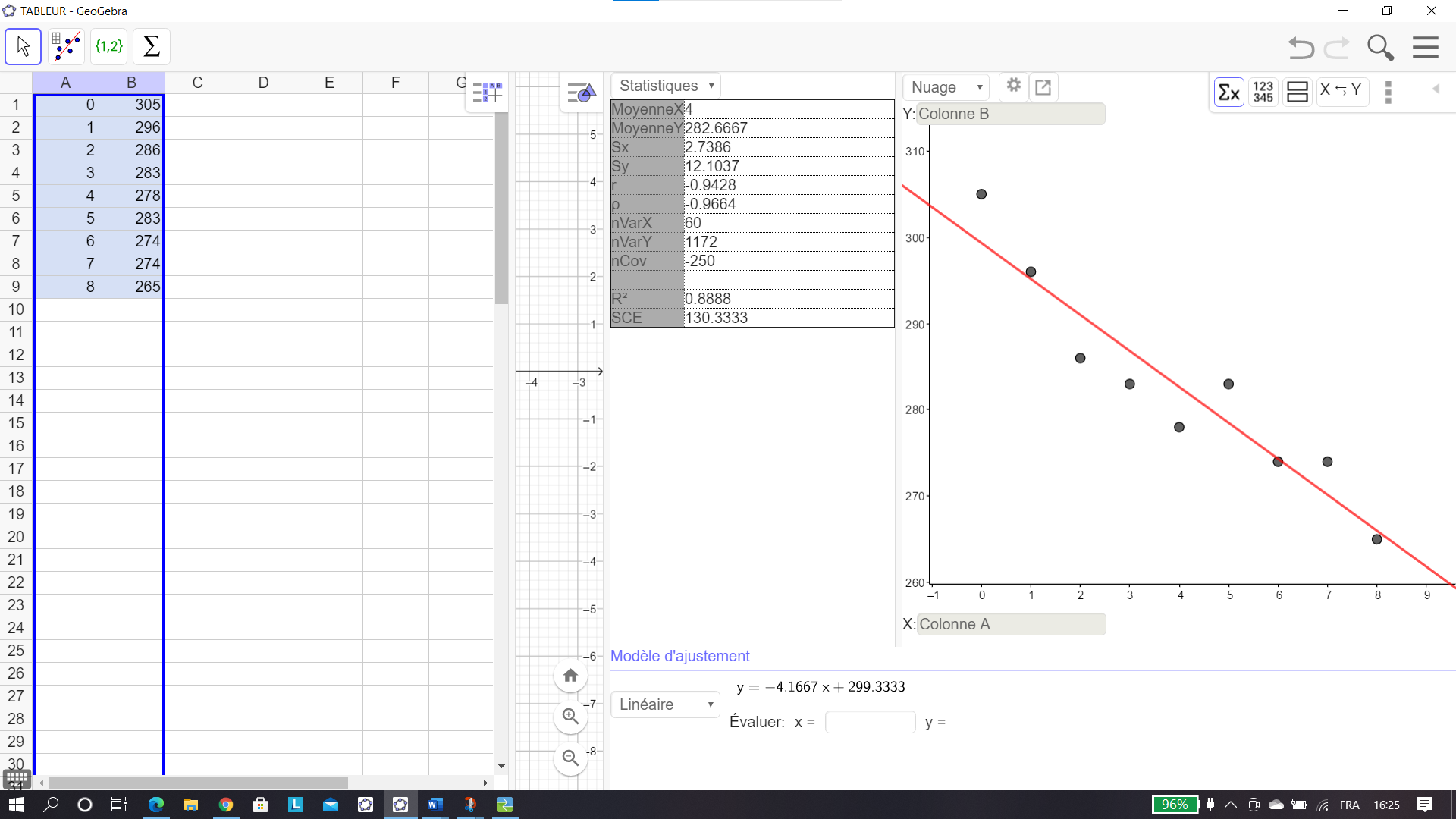
2. Déterminer, à l’aide de la calculatrice, une équation de la droite d’ajustement affine de y en x par la méthode des moindres carrés (on donnera les coefficients sous forme décimale, arrondis au centième).
Tracer cette droite sur le graphique précédent.
Coefficient de corrélation.
Définition : coefficient de corrélation linéaire
Le coefficient de corrélation linéaire d’une série statistique de variables x et y est le nombre r défini par :
r=\frac{cov(x,y)}{\sigma(x)\sigma(y)}.
Propriété :
Le coefficient de corrélation linéaire d’une série statistique r vérifie -1\leq r\leq 1.
- si r=- 1 ou r= 1 alors les points du nuage sont quasiment alignés et l’ajustement affine est adapté.
- si r= 0 les points sont très dispersés autour de la droite et l’ajustement affine n’est pas adapté.
Exercice n°4 : voici une série à deux variables :
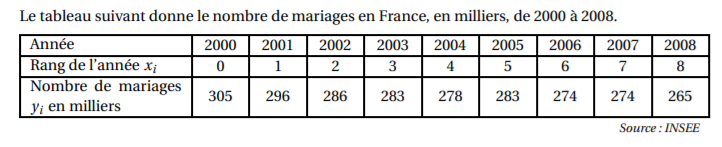
Déterminer r, le coefficient de corrélation linéaire de cette série statistique et tracer la droite d’ajustement affine de y en x par la méthode des moindres carrés.
Ajustement et changement de variable.
Exercice n°5 :
Un centre d’appel comptait en 2001 soixante-six employés. Le tableau ci-dessous donne l’évolution
du nombre d’employés en fonction du rang de l’année.

On cherche à étudier l’évolution du nombre y d’employés en fonction du rang x de l’année.
Une étude graphique montre qu’un ajustement affine ne convient pas.
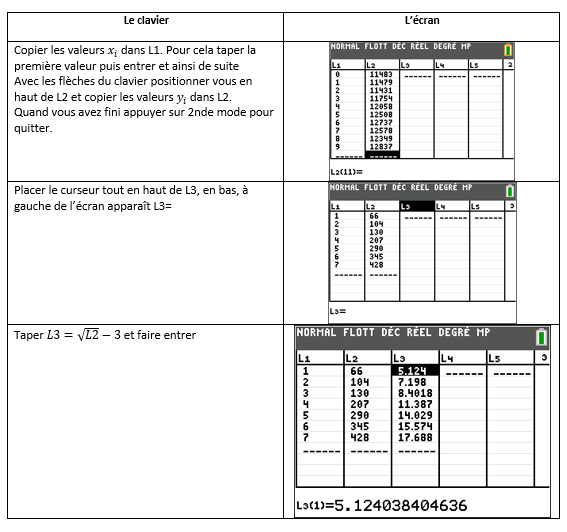
On pose alors z=\sqrt y -3
1. Recopier et compléter le tableau suivant (on donnera les résultats sous forme décimale, arrondis au centième)

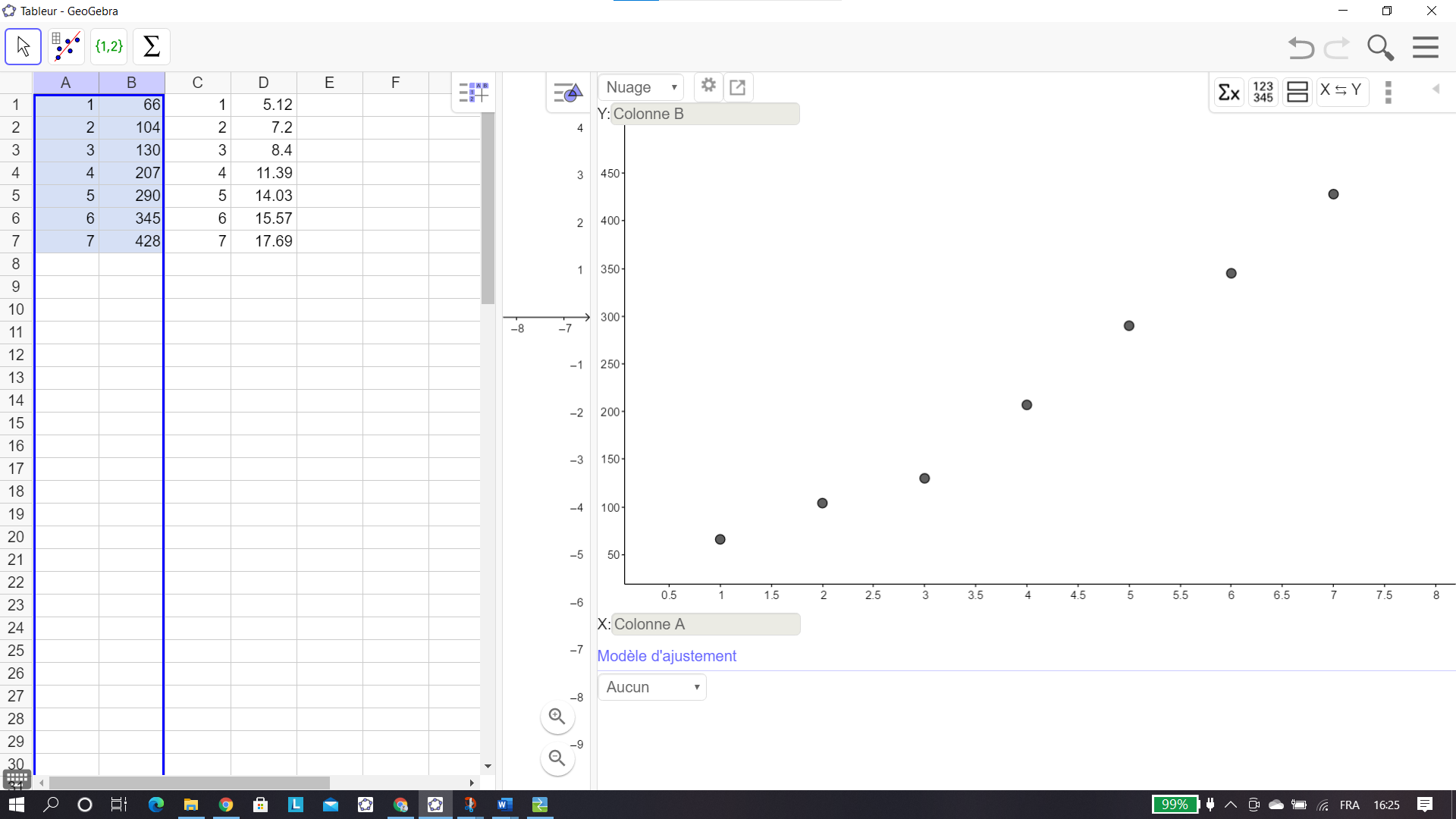
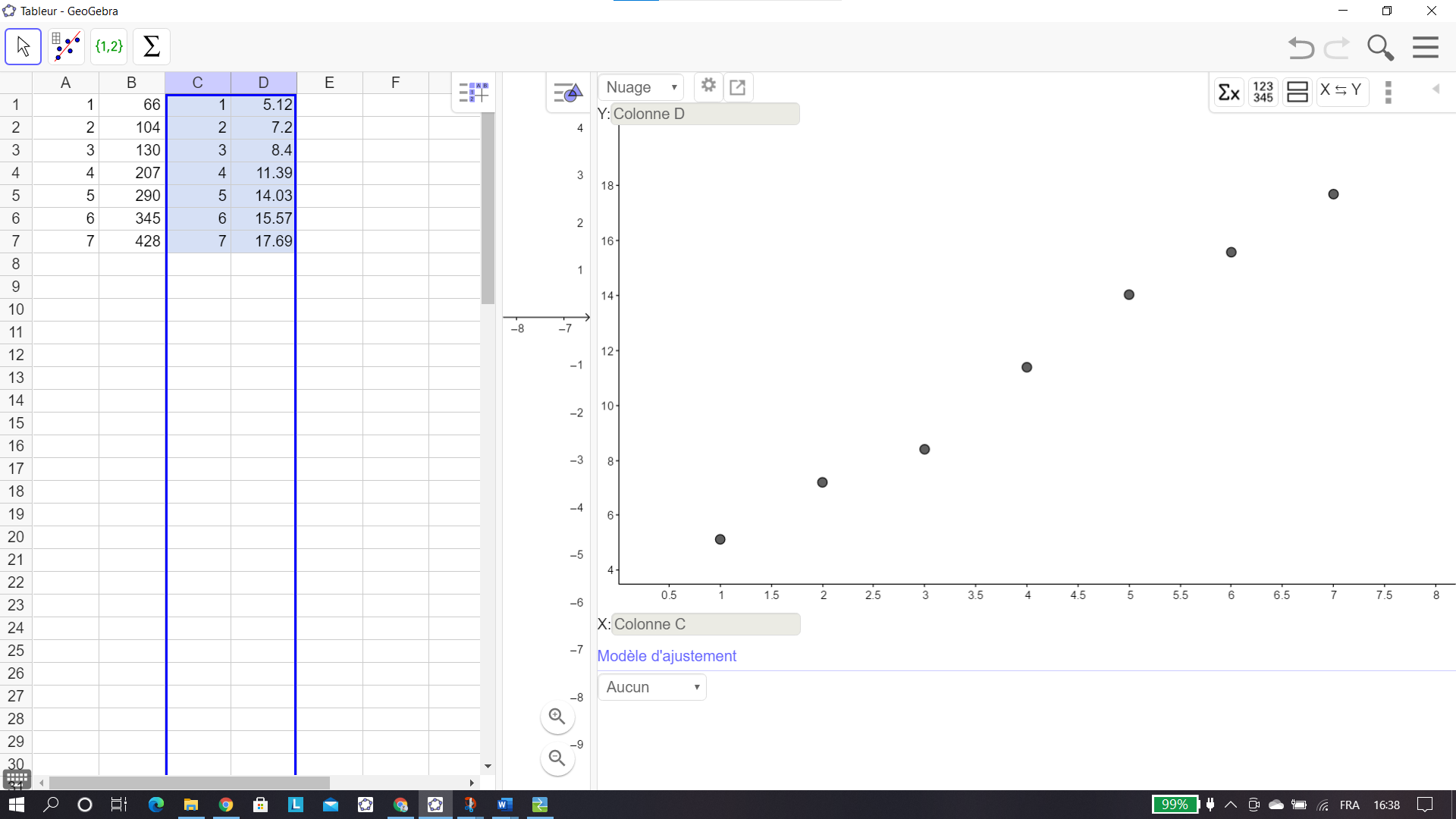
2. Représenter le nuage de points M_i(x_i;z_i) associé à cette série statistique, dans le plan muni
d’un repère orthonormal d’unité graphique 1 cm.
Un ajustement affine vous paraît-il approprié ? Justifier la réponse.
3. Déterminer, à l’aide de la calculatrice, une équation de la droite d’ajustement affine de z en x par la méthode des moindres carrés (on donnera les coefficients sous forme décimale, arrondis
au centième).
Tracer cette droite sur le graphique précédent.
4. En utilisant cet ajustement, à partir de quelle année peut-on prévoir que l’effectif de ce centre
d’appel dépassera 900 employés ?

Exercice n°6 ES Antilles 2008
Le tableau suivant donne l’évolution du nombre d’adhérents d’un club de rugby de 2001 à 2006.

On cherche à étudier l’évolution du nombre y d’adhérents en fonction du rang x de l’année.
Partie A : un ajustement affine.
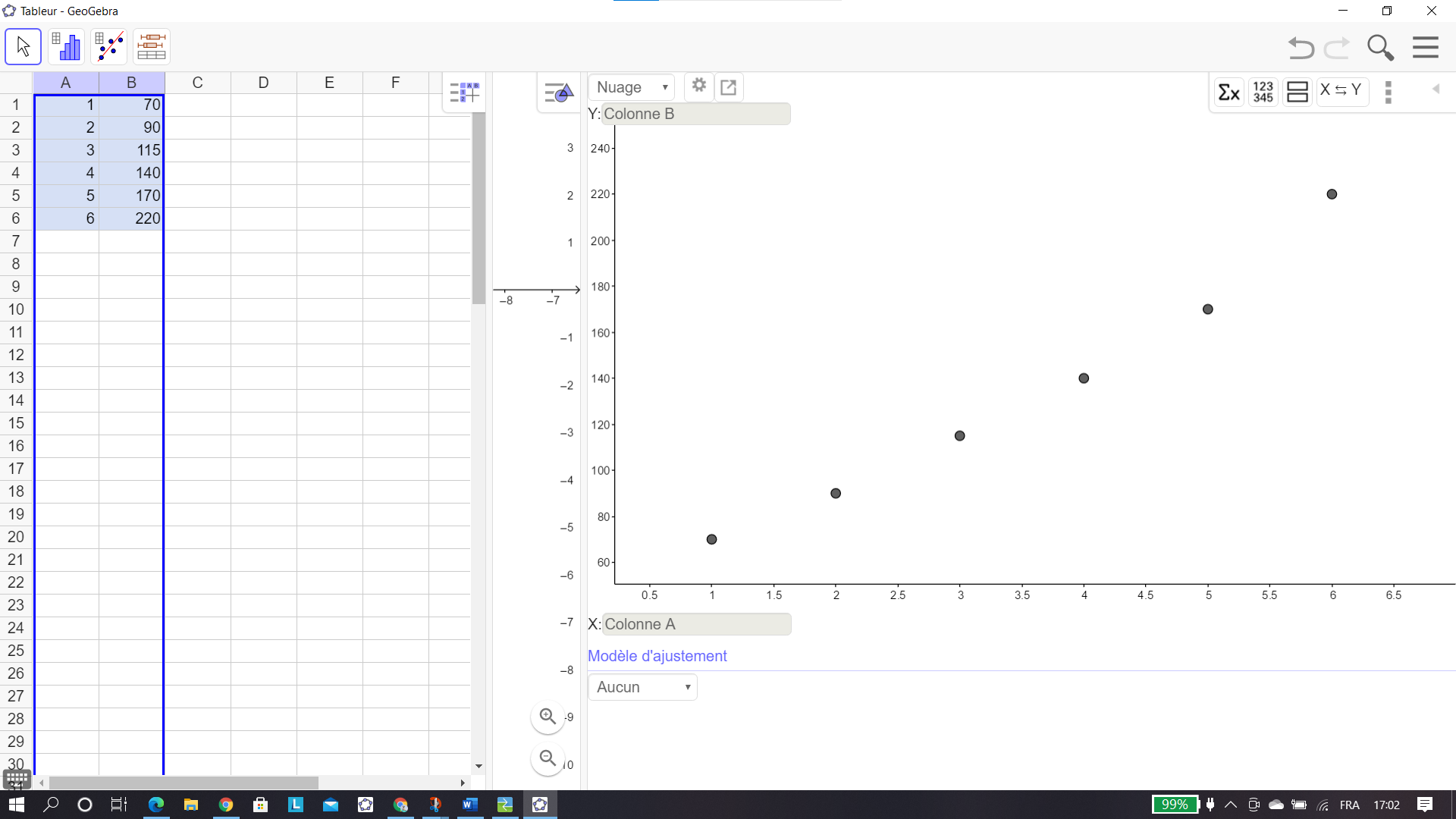
1. Dans le plan muni d’un repère orthogonal d’unités graphiques : 2 cm pour une année sur
l’axe des abscisses et 1 cm pour 20 adhérents sur l’axe des ordonnées, représenter le nuage de
points associé à la série (x_i;y_i)
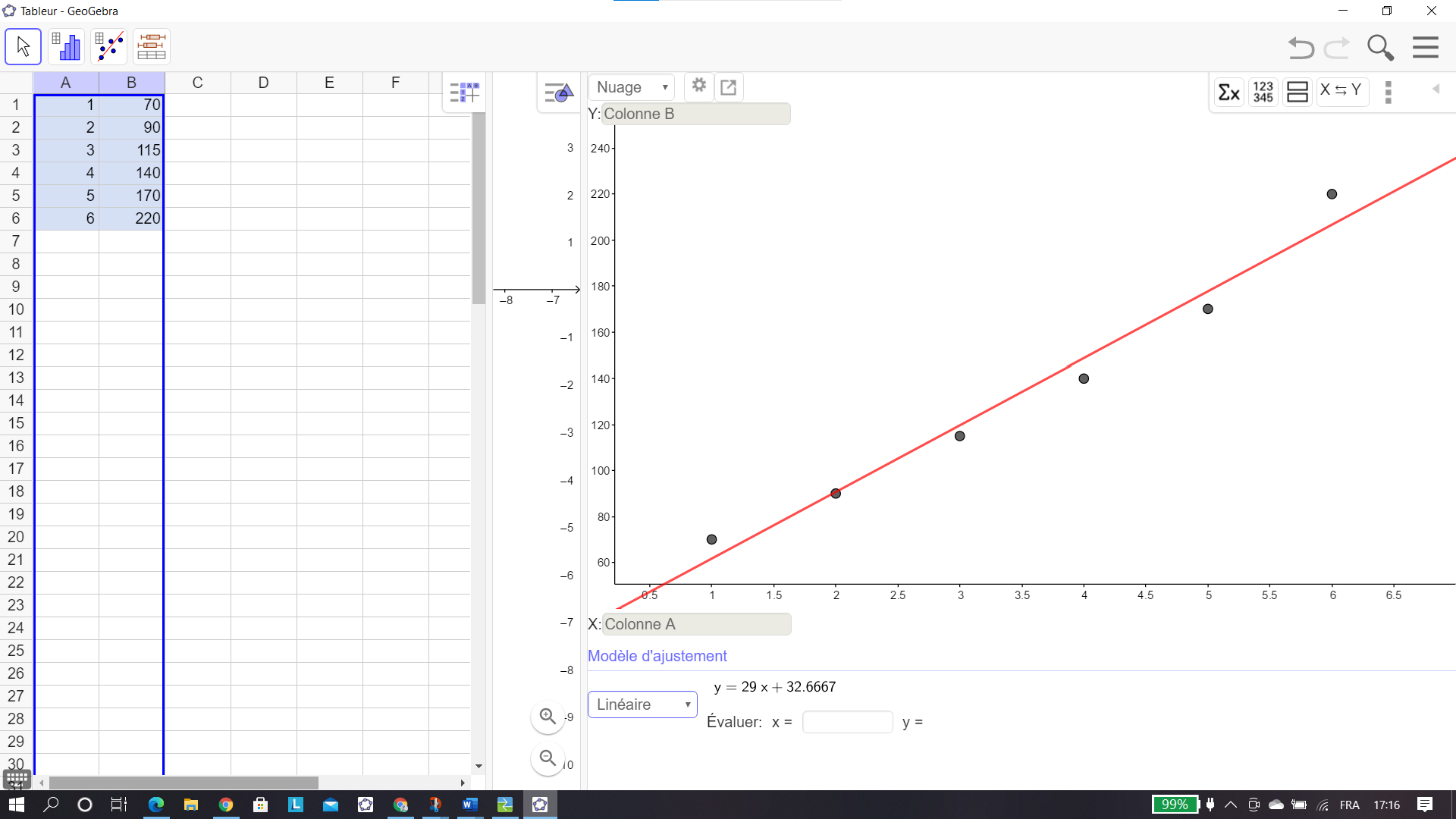
2. Déterminer une équation de la droite d’ajustement de y en x obtenue par la méthode des moindres carrés et la tracer sur le graphique précédent (aucune justification n’est exigée, les
calculs seront effectués à la calculatrice et les coefficients seront arrondis à l’unité).
3. En supposant que cet ajustement reste valable pour les années suivantes, donner une estimation du nombre d’adhérents en 2007.
Partie B : un ajustement exponentiel.
On pose z = ln y.
1. Recopier et compléter le tableau suivant en arrondissant les valeurs de zi au millième.

2. Déterminer une équation de la droite d’ajustement de z en x obtenue par la méthode des moindres carrés (aucune justification n’est exigée, les calculs seront effectués à la calculatrice et les coefficients seront arrondis au millième).
3. En déduire une approximation du nombre d’adhérents y en fonction du rang x de l’année.
4. En prenant l’approximation y\approx 57.1e^{0.224x} et en supposant qu’elle reste valable pour les années suivantes, donner une estimation du nombre d’adhérents en 2007.
Partie C : comparaison des ajustements.
En 2007, il y a eu 280 adhérents. Lequel des deux ajustements semble le plus pertinent ?
Justifier la réponse.

Exercice n°7 : centres étrangers juin 2008 ES
Une association organise chaque année un séjour qui s’adresse à des adultes handicapés. À sa création en 1997, dix adultes handicapés sont partis durant cinq jours. Ainsi, on dira qu’en 1997 le nombre de « journées participant » est de 5\times 10 soit 50.
Le tableau suivant donne le nombre de « journées participant » de 1997 à 2004. L’année 1997 a le rang 0.

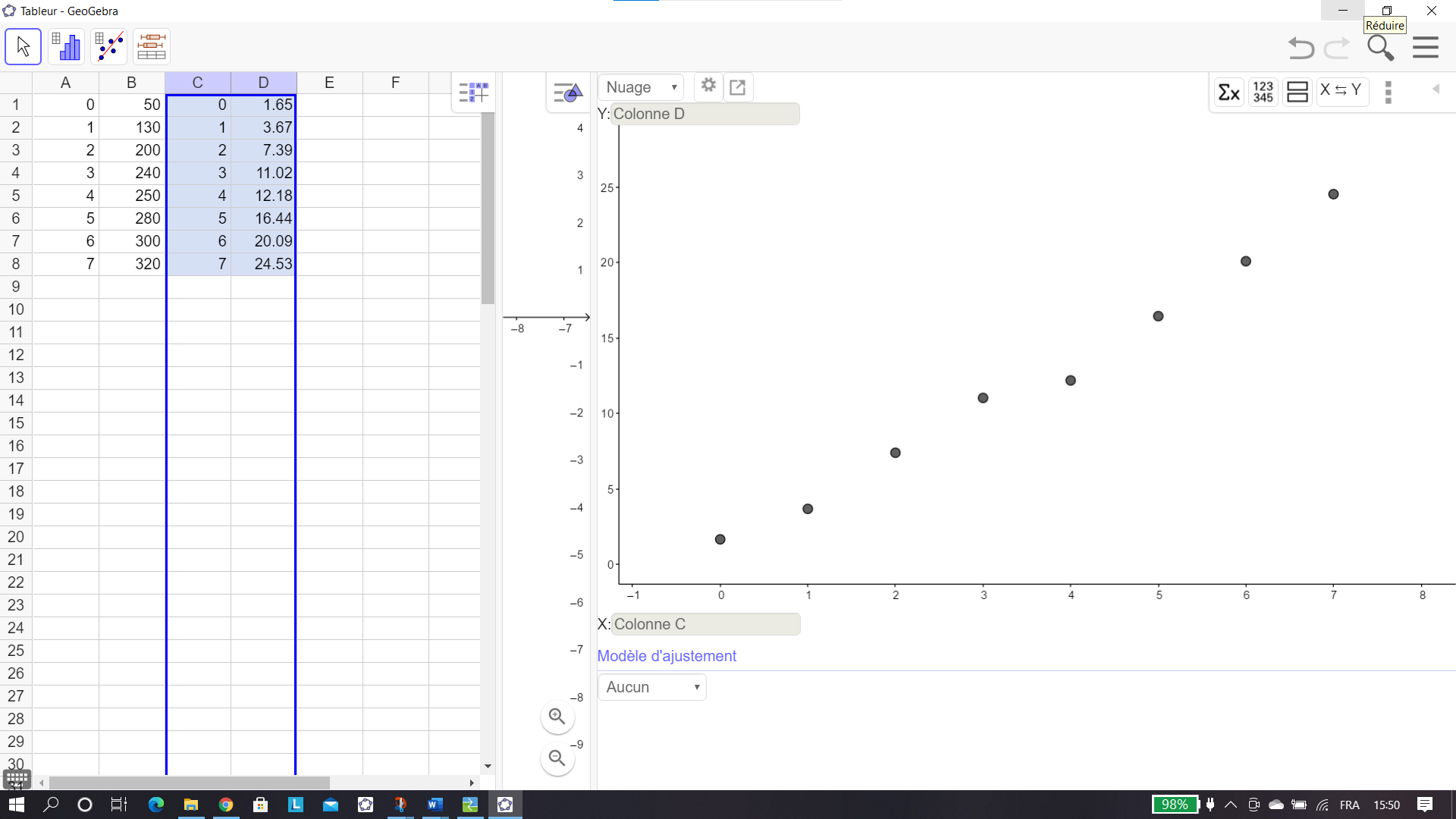
On représente les données à l’aide ce nuage de points :
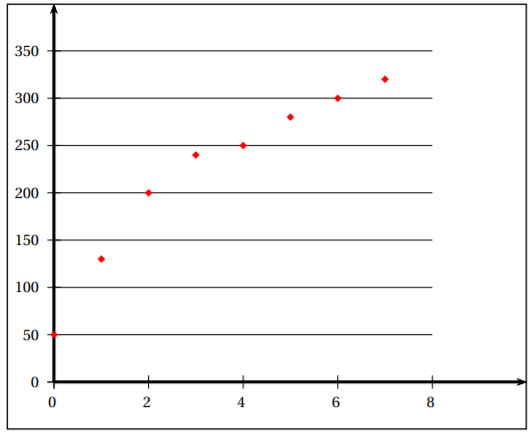
On considère qu’un ajustement affine n’est pas pertinent. L’allure du nuage suggère de chercher un ajustement de y en x de la forme y = k ln(ax +b) où k, a, b sont trois nombres réels.
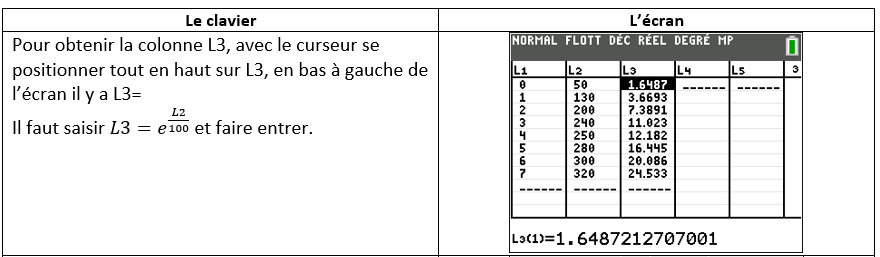
Pour cela on pose z_i= e^{\frac{y_i}{100}}
Dans cette question les calculs seront effectués à la calculatrice. Aucune justification n’est demandée. Les résultats seront arrondis au centième.
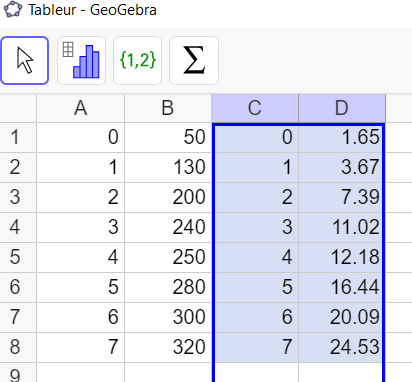
1.a. Recopier et compléter le tableau suivant :

b. Représenter le nuage de points associé à la série (x_i;z_i) dans un repère orthonormal.
c. Donner les coordonnées du point moyen.
d. Déterminer une équation de la droite D d’ajustement affine de z en x par la méthode des moindres carrés. Représenter la droite D sur le graphique.
e. Sachant que z_i=e^{\frac{y_i}{100}} déterminer l’expression de y en fonction de x.
2. On suppose que l’évolution du nombre de « journées participant » se poursuit dans un futur
proche selon le modèle précédent.
Estimer, à l’unité près, quel serait le nombre de « journées participant » prévu pour l’année
2007.
Interpolations et extrapolations.
Vocabulaire : Lorsqu’on utilise un ajustement pour estimer
en dehors du nuage de points, on fait une extrapolation.
à l’intérieur du nuage de points, on fait une interpolation.
Exemples d’extrapolations : Exercice n°5, question 4; Exercice n°6, question 4 ; Exercice n°7, question 2.
Exercice n°8 : Distance de freinage
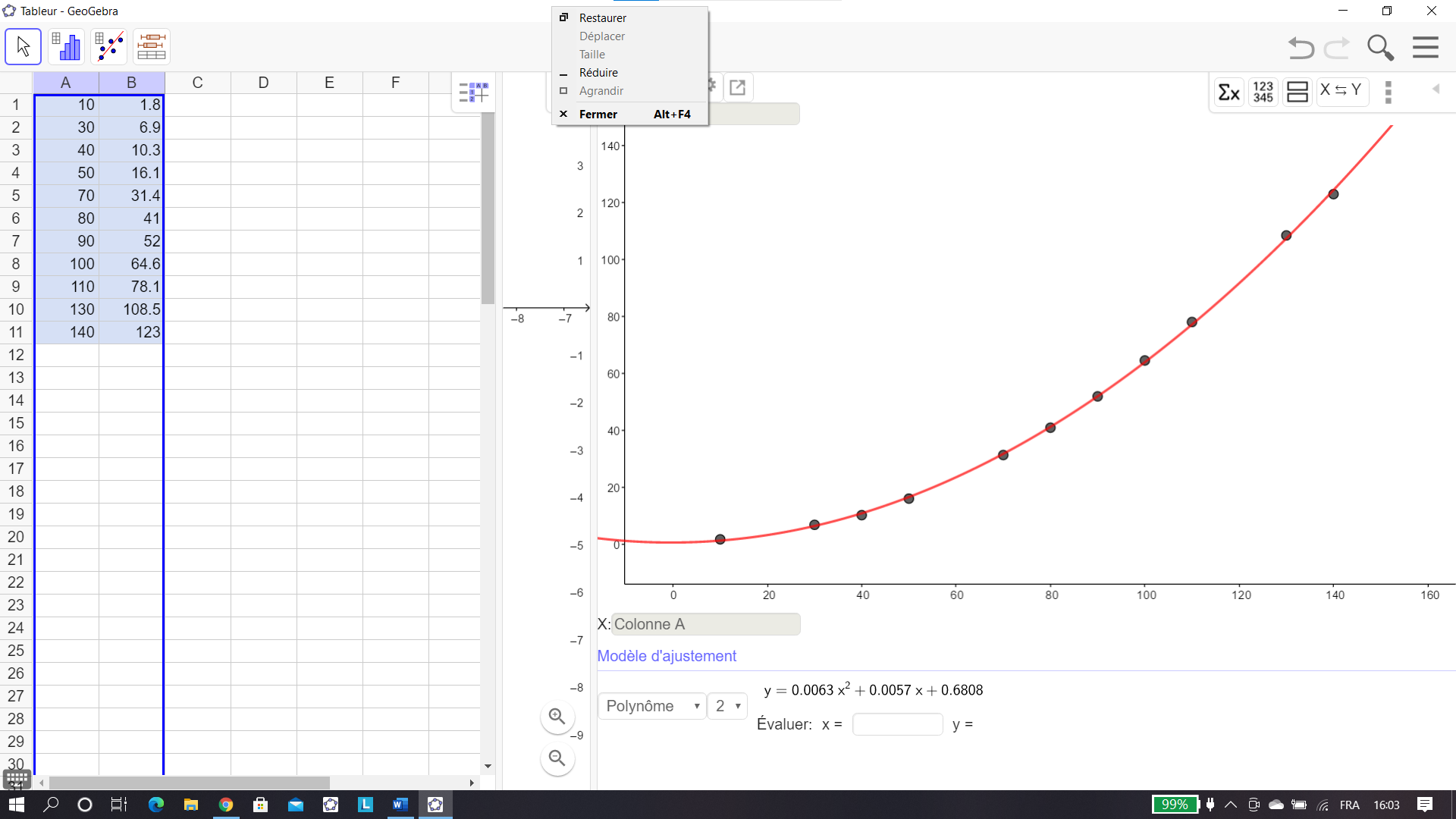
Voici un document de la sécurité routière.

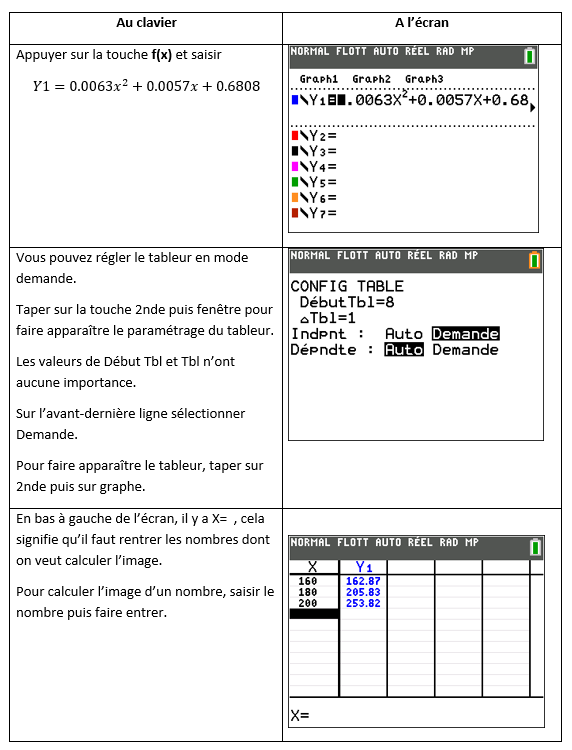
- A l’aide du logiciel Géogébra, déterminer un ajustement par une fonction du second degré.
2. Interpolation (on estime la distance de freinage pour des vitesses comprises entre 10 et 140)
Déterminer à l’aide de l’ajustement précédent les distances de freinage pour les vitesses 20km/h, 60km/h et 120 km/h.
3. Extrapolation (on estime la distance de freinage pour des vitesses non comprises entre 10 et 140)
Déterminer à l’aide de l’ajustement précédent les distances de freinage pour les vitesses 160km/h, 180km/h et 200 km/h.