Equations cartésiennes d’une droite de vecteur normal \overrightarrow{n}
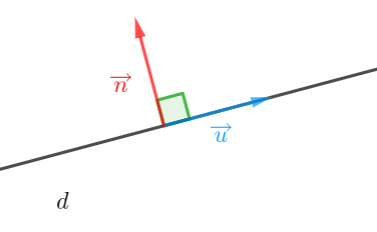
Définition
Un vecteur \overrightarrow{n} est dit normal à une droite d si \overrightarrow{n} est orthogonal à un vecteur directeur de la droite d.
Propriété :
- Une droite d de vecteur normal \overrightarrow{n}(a;b) a une équation cartésienne de la forme ax+by+c=0 où c est un nombre réel.
- La droite d d’équation cartésienne ax+by+c=0 avec (a;b)\ne (0;0) admet le vecteur \overrightarrow{n}(a;b) pour vecteur normal.
Démonstration de la première propriété
Chercher l’équation cartésienne d’une droite c’est chercher une relation du type ax+by+c=0 reliant x et y les coordonnées d’un point M quelconque situé sur la droite d.
Faisons un schéma :

Le point M appartient à la droite d si et seulement si \overrightarrow{AM}.\overrightarrow{n}=0.
On va utiliser la forme analytique du produit scalaire. Il faut donc calculer les coordonnées du vecteur \overrightarrow{AM}.
\hspace{0.5cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2.2cm}x_{M}\hspace{0.1cm}y_{M}
A(x_A;y_A)\hspace{2cm}M(x;y)
J’écris la formule : \overrightarrow{AM}(x_{M}-x_{A};y_{M}-y_{A})
\overrightarrow{AM}(x-x_{A};y-y_{A})
On rappelle que \overrightarrow{n}(a;b)\\\overrightarrow{MA}.\overrightarrow{MB}=0\\a(x-x_A)+b(y-y_A)=0\\ax-ax_A+by-by_A=0\\ax+by-ax_A-by_A=0
Ainsi l’équation cartésienne de la droite d est ax+by-ax_A-by_A=0
Démonstration de la seconde propriété
On a vu en classe de seconde que la droite d d’équation ax+by+c=0 a pour vecteur directeur \overrightarrow{u}(-b;a).
Calculons le produit scalaire \overrightarrow{u}.\overrightarrow{n}=a\times(-b)+b\times a =0. Donc le vecteur \overrightarrow{n}(a;b) est bien normal à la droite d.
Vous pourrez utiliser cette fenêtre Géogébra pour valider vos réponses aux exercices.
Exercice n°1
d est une droite qui passe par A(6;2) et de vecteur normal \overrightarrow{n}(-2;5).
Pour placer A, saisir dans la colonne de gauche A=(6,2). Attention bien saisir une virgule entre les coordonnées.
Pour tracer le vecteur \overrightarrow{n}(-2;5). Cliquer sur le troisième onglet à partir de la gauche et sélectionner vecteur dans le menu déroulant. Puis dans le repère cliquer sur A, avancer horizontalement de 2 graduations vers la gauche et monter de 5 graduations puis cliquer.
Pour tracer la droite d, cliquer sur le quatrième onglet à partir de la gauche et sélectionner Perpendiculaire dans le menu déroulant. Puis dans le repère cliquer sur A et sur le vecteur \overrightarrow{n}. la droite apparaît et son équation dans la colonne de gauche. Pour obtenir une équation cartésienne, cliquer gauche sur l’équation affichée et choisir Equation ax+by+c=0
Déterminer une équation cartésienne de d.
Exercice n°2
d est une droite qui passe par A(4;-1) et de vecteur normal \overrightarrow{n}(3;2).
Déterminer une équation cartésienne de d.
Exercice n°3
On donne A(2;3) et B(-1;-3).
Déterminer une équation cartésienne de d la droite perpendiculaire à (AB) passant par A.
Exercice n°4
On donne A(2;3) , B(-1;-3) et C(4;1).
Déterminer une équation cartésienne de la hauteur issue de A dans le triangle (ABC).
Exercice n°5
On donne A(1;3) et B(-1;2).
Déterminer une équation cartésienne de la médiatrice du segment [AB].
Exercice n°6
d_1 est la droite qui passe par A(1;2) et de vecteur normal \overrightarrow{n_1}(3;2).
d_2 a pour équation cartésienne 4x-6y-1=0
- Déterminer un vecteur normal \overrightarrow{n_2} à la droite d_2.
2. Démontrer que les droites d_1 et d_2 sont perpendiculaires.
Equations cartésiennes d’un cercle.
Propriété
C est un cercle de centre A(x_A;y_A) et de rayon r.
Une équation cartésienne de C est (x-x_A)^2+(y-y_A)^2=r^2.
Démonstration
M(x;y) appartient au cercle C si et seulement si AM=r
\hspace{6.5cm}AM^2=r^2
On a vu en classe de seconde que AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}.
\hspace{4cm}(x-x_A)^2+(y-y_A)^2=r^2.
Ainsi l’équation du cercle est bien (x-x_A)^2+(y-y_A)^2=r^2.
Exercice n°7
Dans chaque cas, déterminer une équation cartésienne du cercle C de centre A et de rayon r.
Conjecturer le résultat avant de se lancer dans les calculs avec la fenêtre géogébra ci-dessous. Voyons ce que ça donne pour l’exo7.1
Placer le point A en tapant A=(1,3) dans la colonne de gauche.
Tracer le cercle de centre A et de rayon 2 en cliquant sur le sixième onglet et en sélectionnant Cercle (centre-rayon) dans le menu déroulant.Ensuite dans le repère, cliquer sur le point A et saisir 2 dans le cadre qui apparaît à l’écran. Dans la colonne de gauche apparaît une équation cartésienne du cercle : (x-1)^2+(y-3)^2=4.
- A(1;3) et r=2
2. A(-2;-5) et r=7
3. A(-1;0) et r=\sqrt{3}
4. A(0;5) et r=2
Exercice n°8
Dans chaque cas, déterminer une équation cartésienne du cercle C de diamètre [AB].
- A(1;3) et B(-1;5).
2. A(0;3) et B(4;-1).
Exercice n°9
C est l’ensemble d’équation x^2+y^2-4x+6y=18 .
- Compléter les pointillés :
x^2-4x=(x-…)^2-… et y^2+6y=(y+…)^2-…
2. En déduire que C est un cercle dont on donnera le centre et son rayon.
Exercice n°10
C est l’ensemble d’équation x^2+y^2-2x+8y-6=0 .
- Compléter les pointillés :
x^2-2x=(x-…)^2-… et y^2+8y=(y+…)^2-…
2. En déduire que C est un cercle dont on donnera le centre et son rayon.
Exercice n°11
C est l’ensemble d’équation x^2+y^2+x=0.
- Compléter les pointillés : x^2+x=(x+…)^2-…
2. En déduire que C est un cercle dont on donnera le centre et son rayon.



