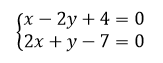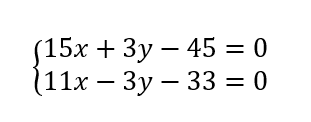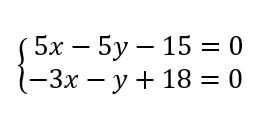logo

1. Exercices types évaluation fin d’année : géométrie repérée.

Utiliser cette fenêtre Géogébra pour faire la figure pour chaque exercice.

Exercice n°1

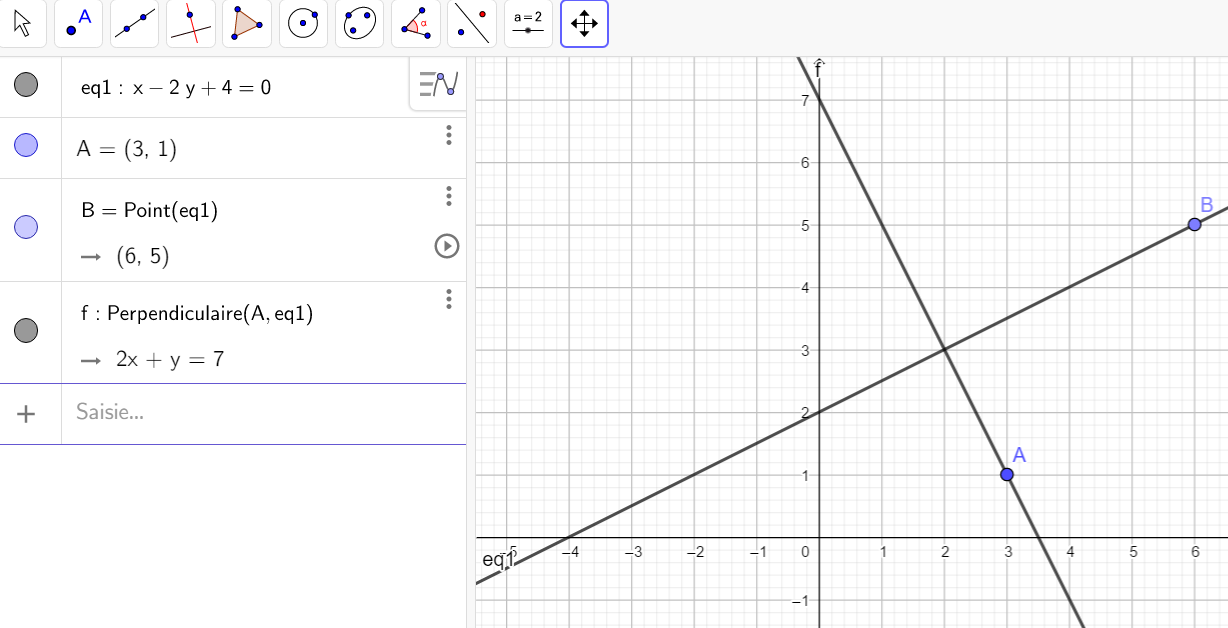
Dans le plan muni d’un repère orthonormé, on considère le point A(3;1) 
ainsi que la droite d d’équation cartésienne x-2y+4=0.

On utilise la page Géogébra au début de la fiche qui permettra de faire la figure au fur et à mesure. Elle permettra aussi de conjecturer les réponses aux différentes questions. 

Pour tracer d, saisir x-2y+4=0 sur la ligne 1 dans la colonne de gauche.

Pour placer A, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Point dans le menu déroulant et dans le repère cliquer au point de coordonnées (3;1).

1. Déterminer les coordonnées du point B d’abscisse 6 appartenant à la droite d.

Pour placer B, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Point dans le menu déroulant et dans le repère cliquer sur la droite au point d’abscisse 6. Dans la colonne de gauche les coordonnées de B s’affichent. On a conjecturé le résultat.

correction

2. Donner les coordonnées d’un vecteur normal à la droite d.

correction

3. Déterminer une équation de la droite \Delta perpendiculaire à la droite d passant par le point A.

Pour tracer \Delta, cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Perpendiculaire dans le menu déroulant et dans le repère cliquer sur la droite d et sur le point A. Dans la colonne de gauche l’équation de \Delta s’affiche. On a conjecturé le résultat.

conjecture graphique avec Géogébra
correction

4. Calculer les coordonnées du projeté orthogonal H du point A sur la droite d.

Pour placer H, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur la droite d et sur la droite \Delta. Dans la colonne de gauche les coordonnées de  H s’affichent. On a conjecturé le résultat.

correction

5. Calculer la distance AH et en donner une interprétation.

Pour mesurer la distance  AH, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point A et sur le point H. La distance AH s’affiche. On a conjecturé le résultat.

correction

Exercice n°2 

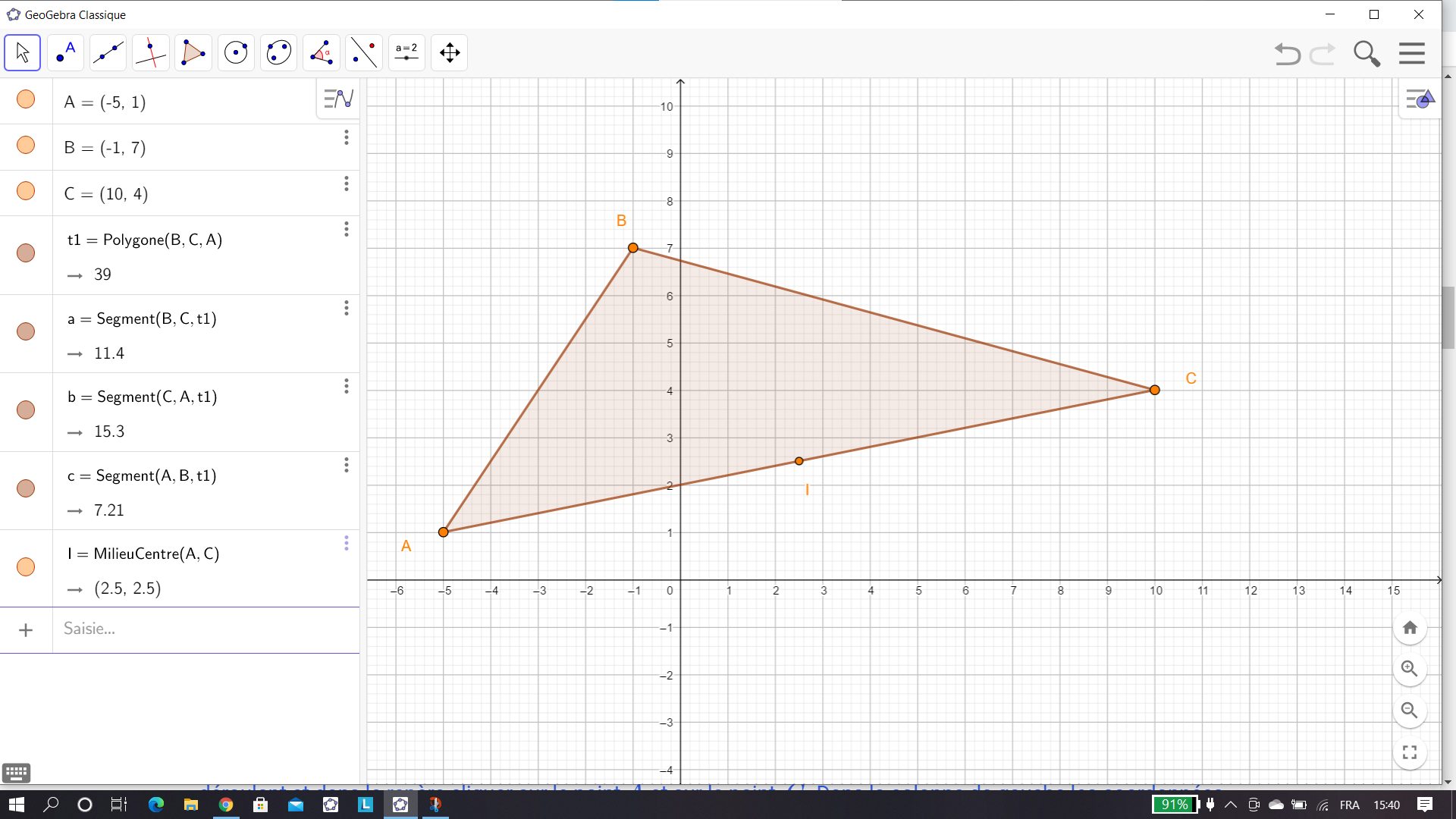
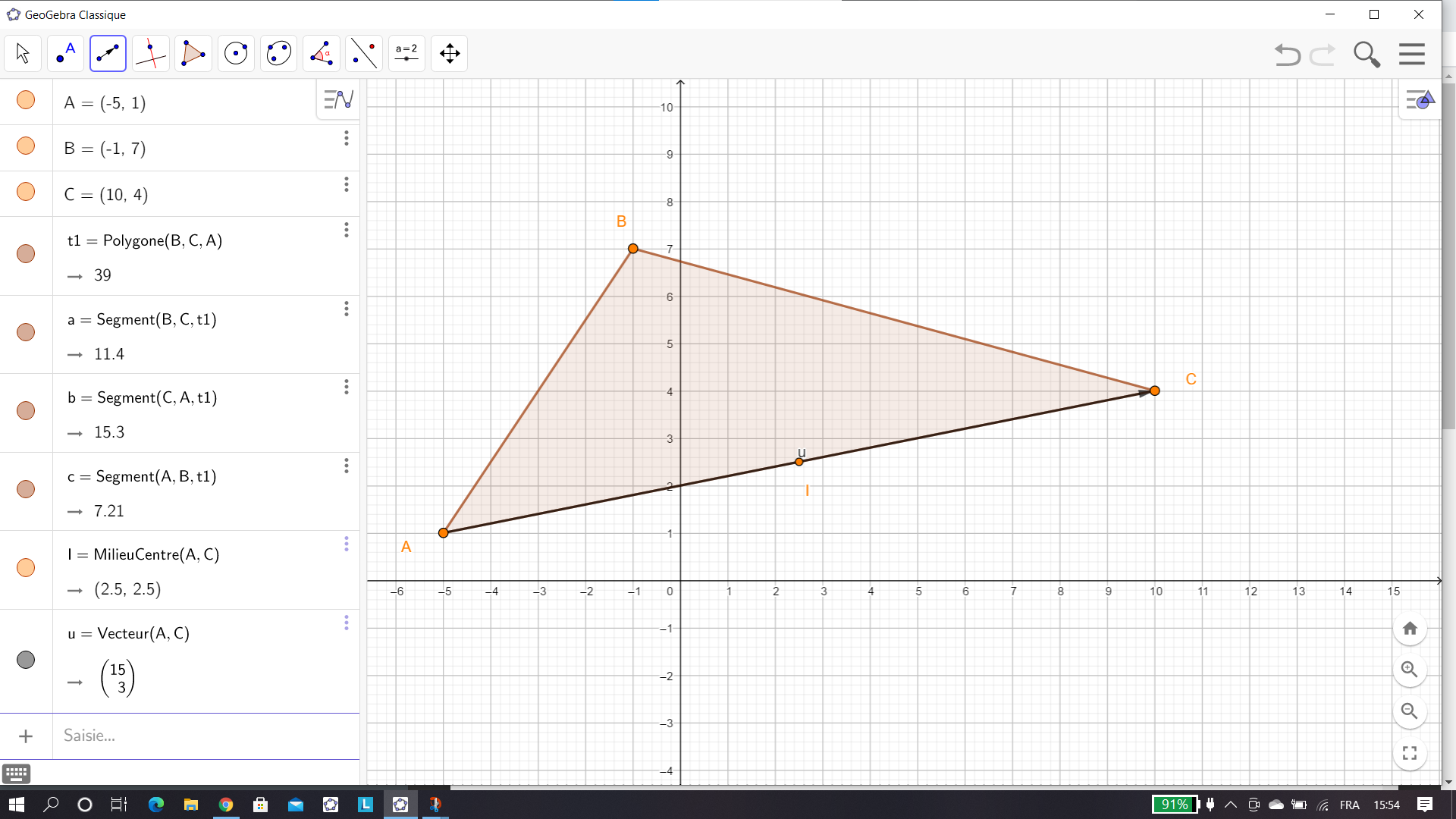
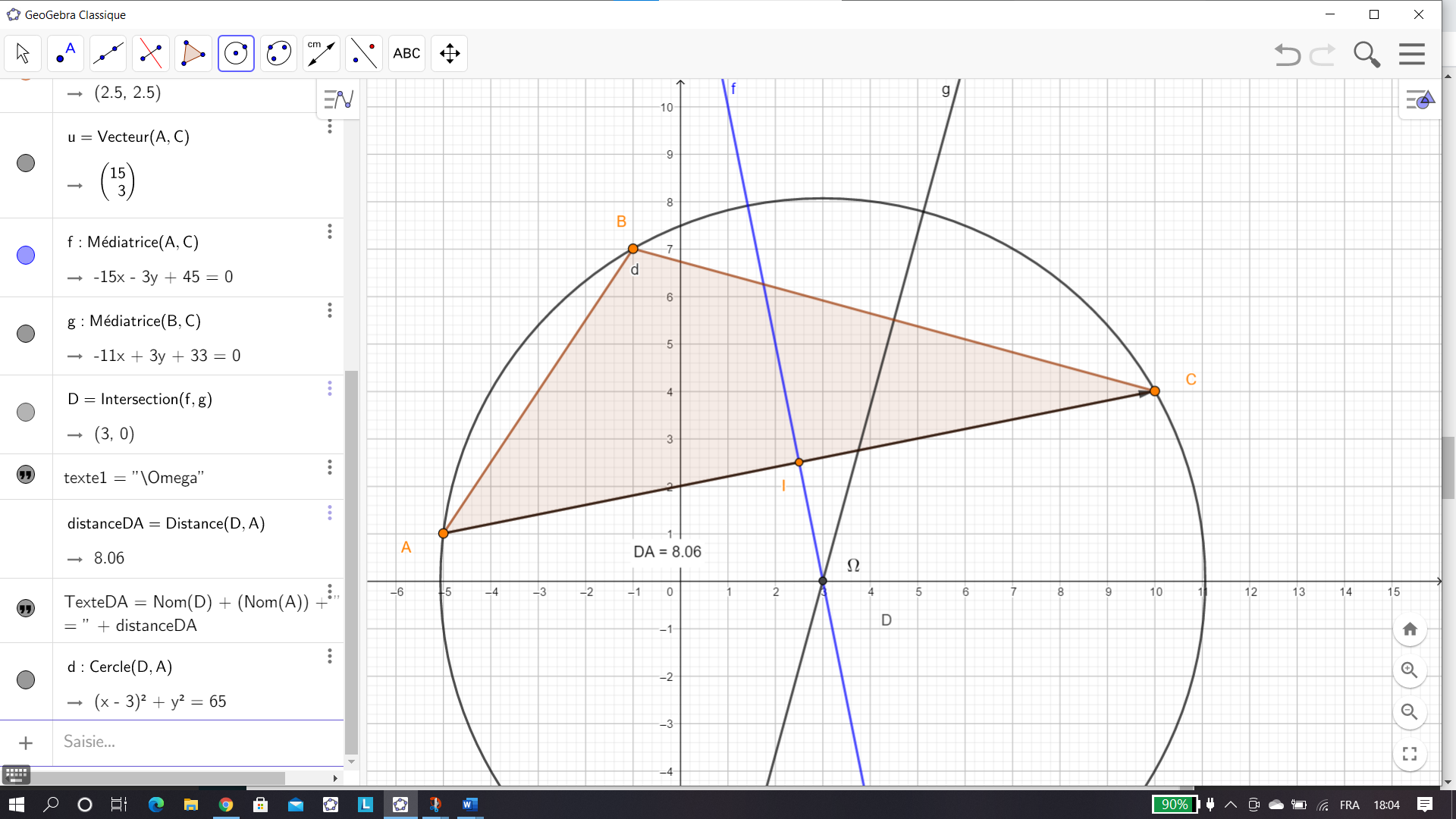
On considère les points A(-5;1), B(-1;7) et C(10;4) dans un repère orthonormé.
On rappelle que le cercle circonscrit à un triangle est le cercle passant par les trois sommets
de ce triangle.
1. a) Déterminer par le calcul, les coordonnées de I, le milieu du segment [AC]. 

Pour placer I, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Milieu ou centre dans le menu déroulant et dans le repère cliquer sur le point A et sur le point  C. Dans la colonne de gauche les coordonnées de  I s’affichent. On a conjecturé le résultat.

correction

1. b) Déterminer par le calcul, les coordonnées du vecteur \overrightarrow{AC}.

Pour tracer \overrightarrow{AC}, cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Vecteur  dans le menu déroulant et dans le repère cliquer sur le point A et sur le point  C. Dans la colonne de gauche les coordonnées du vecteur  \overrightarrow{AC} s’affichent. On a conjecturé le résultat.

correction

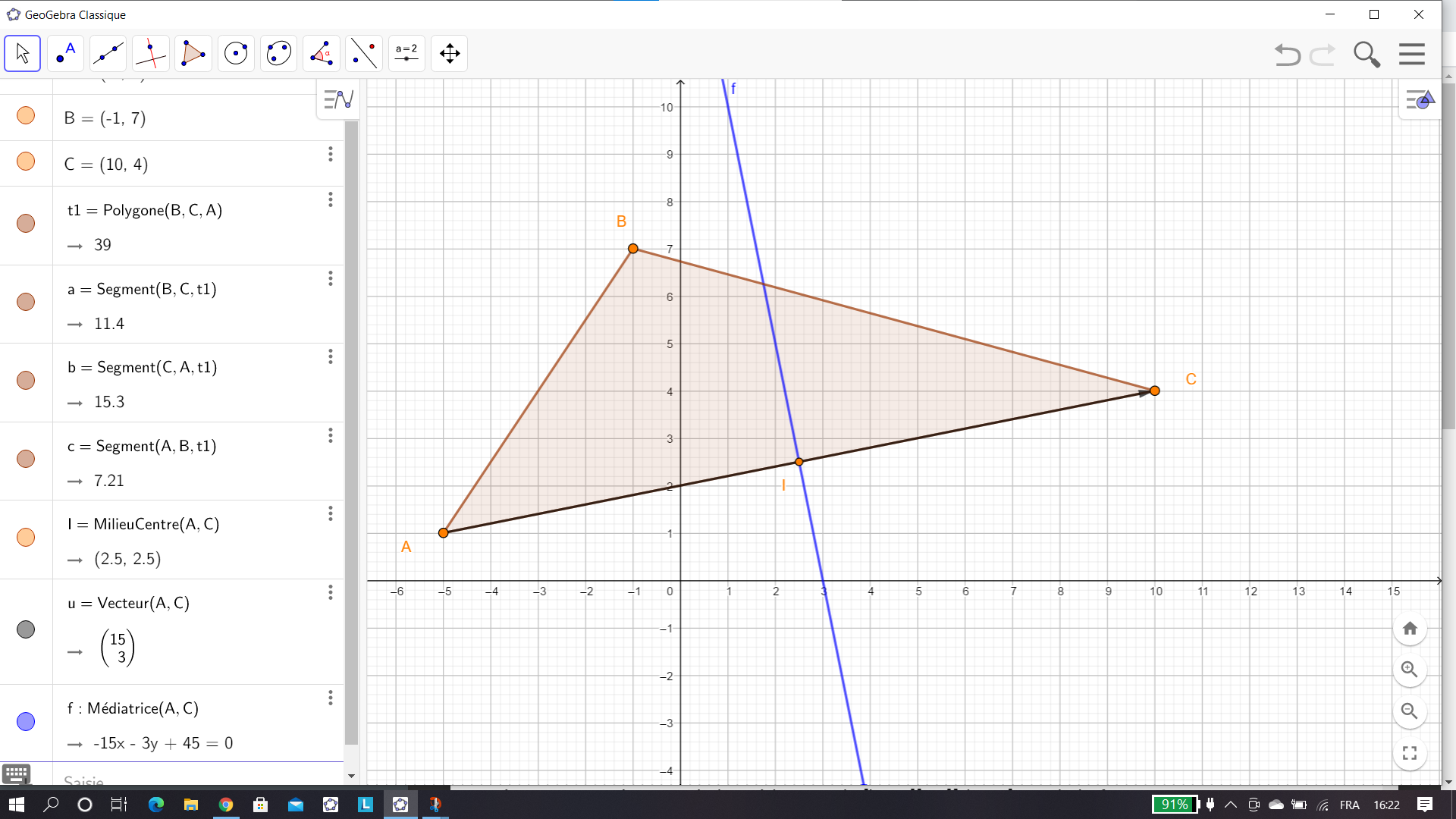
1. c) Déduire des questions précédentes, l’équation cartésienne de la médiatrice du segment [AC].

Pour tracer la médiatrice de (AC), cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Médiatrice dans le menu déroulant et dans le repère cliquer sur le point A et sur le point  C. Dans la colonne de gauche l’équation cartésienne de la médiatrice de   [AC] s’affiche. On a conjecturé le résultat.

correction

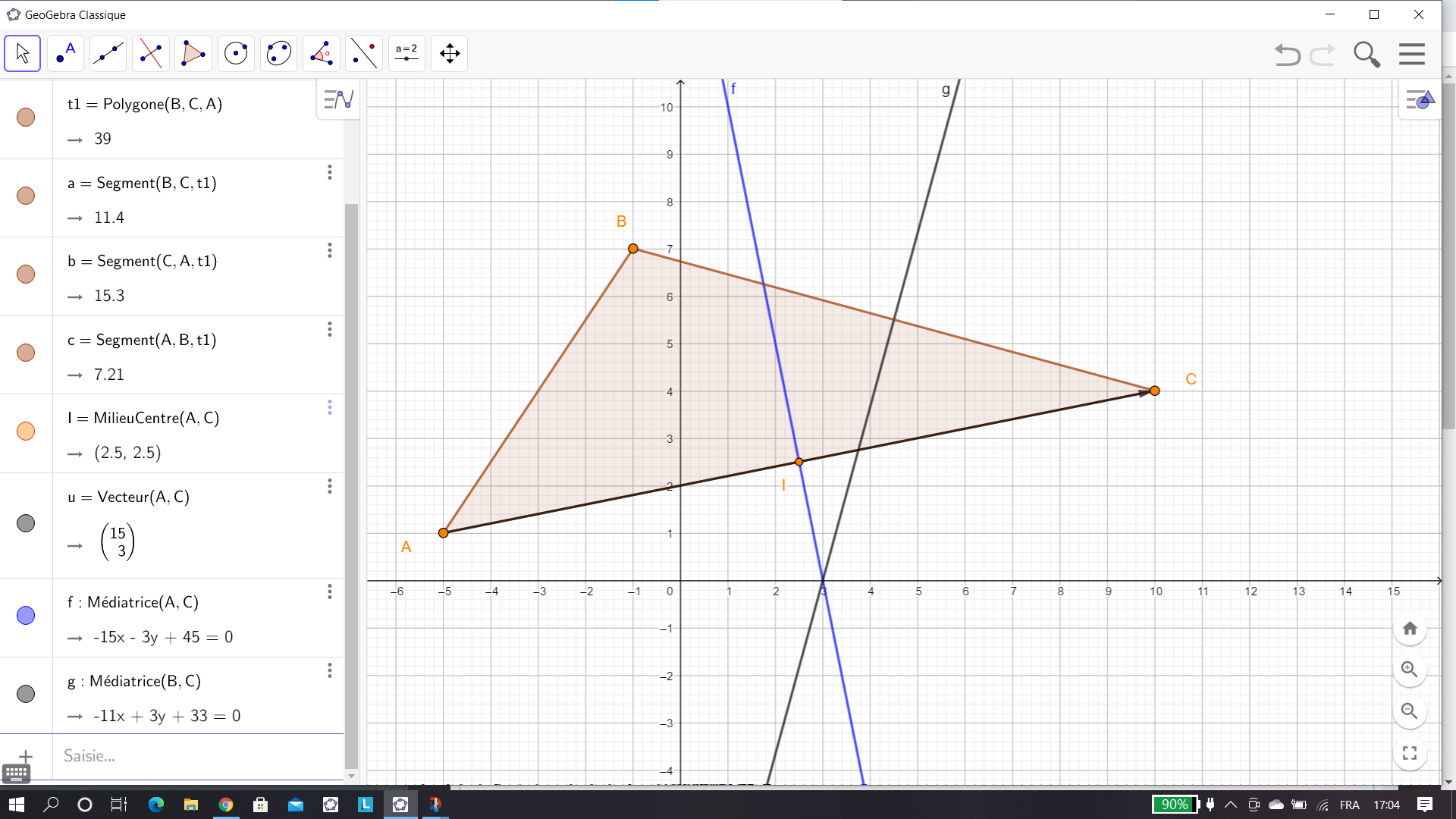
2. Déterminer une équation cartésienne de la médiatrice du segment [BC].

Pour tracer la médiatrice de (BC), cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Médiatrice dans le menu déroulant et dans le repère cliquer sur le point B et sur le point  C. Dans la colonne de gauche l’équation cartésienne de la médiatrice de   [AC] s’affiche. On a conjecturé le résultat.

correction

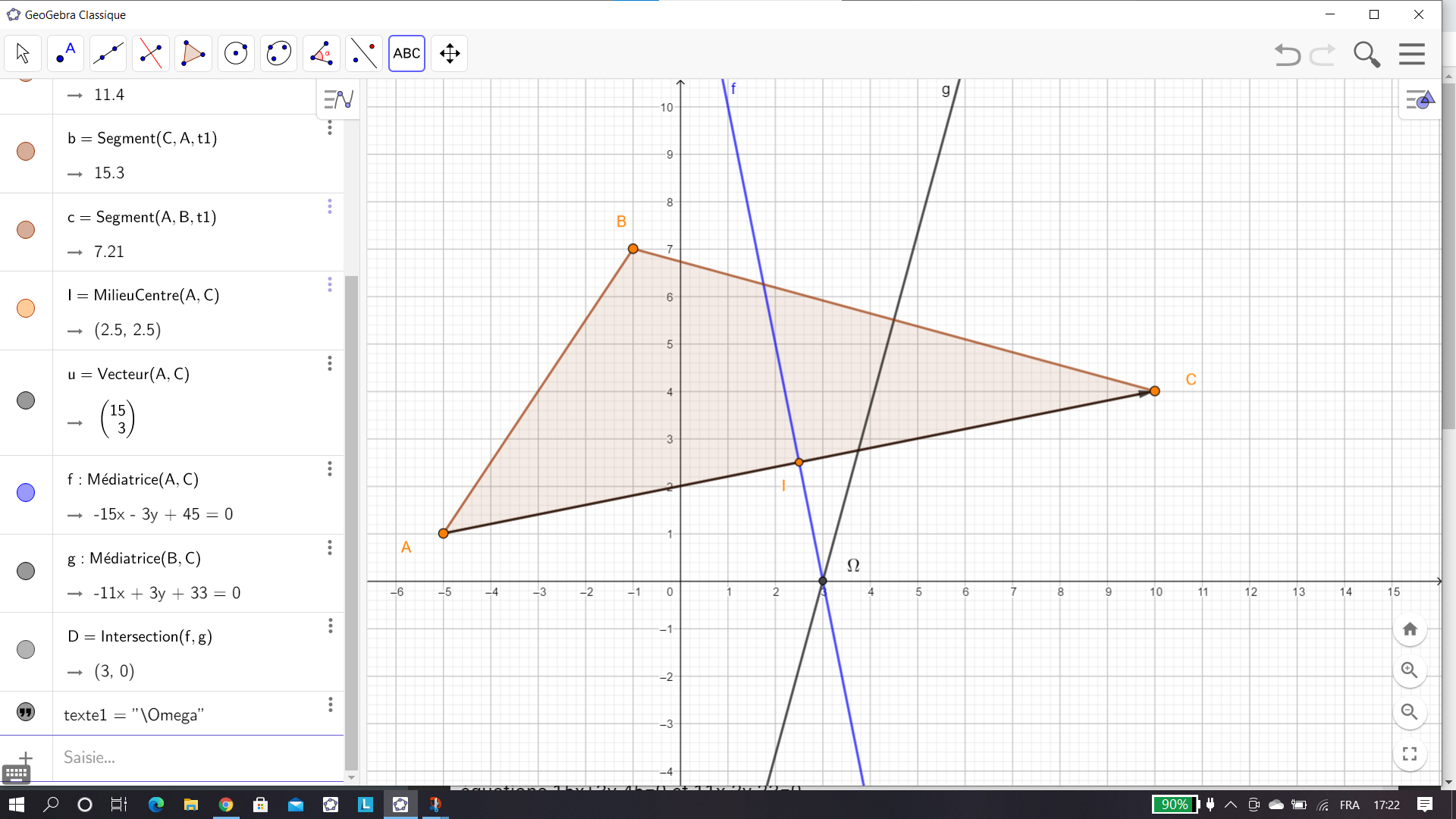
3. Déduire des questions précédentes les coordonnées du centre du cercle circonscrit \Omega au triangle ABC.

Pour placer \Omega qui est le point d’intersection des médiatrices, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur les deux médiatrices. Dans la colonne de gauche les coordonnées de \Omega s’affichent. On a conjecturé le résultat.

correction

4.a) Calculer le rayon du cercle circonscrit au triangle ABC

Pour mesurer la distance  \OmegaA, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point \Omega et sur le point A. La distance \OmegaA s’affiche.

correction

4.b) Déterminer l’équation du cercle circonscrit au triangle ABC.

Pour tracer le cercle circonscrit à ABC , cliquer sur le 6ème onglet en haut à partir de la gauche, sélectionner Cercle (centre-point) dans le menu déroulant et dans le repère cliquer sur le point \Omega et cliquer sur le point A. Dans la colonne de gauche l’équation du cercle s’affiche. On a conjecturé le résultat.

correction

Exercice 3

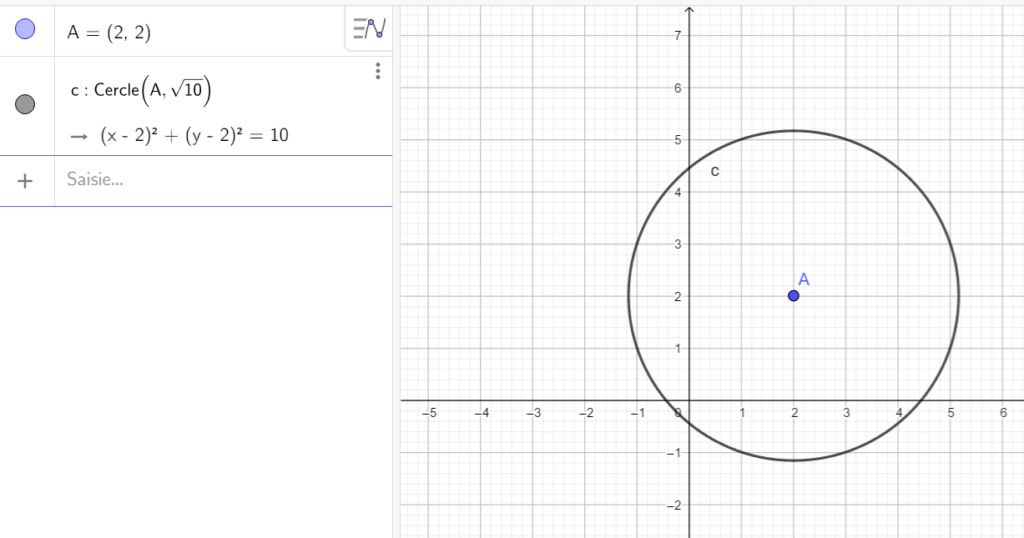
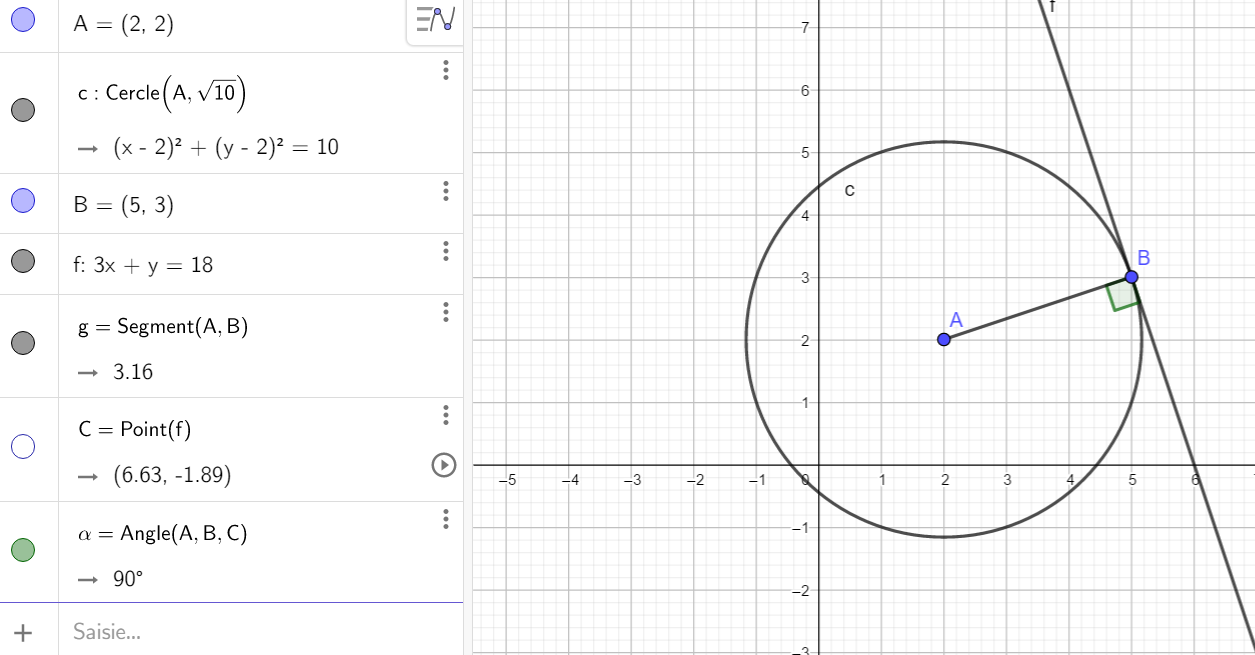
Dans un repère orthonormé, on considère le cercle  C de centre  A(2;2) et de rayon  \sqrt{10}.
1. Déterminer l’équation cartésienne du cercle C.

Pour tracer le cercle C , cliquer sur le 6ème onglet en haut à partir de la gauche, sélectionner Cercle (centre-rayon) dans le menu déroulant et dans le repère cliquer sur le point A et saisir sqrt(10) dans le cadre qui est situé sous le mot rayon. Dans la colonne de gauche l’équation du cercle s’affiche. On a conjecturé le résultat.

correction

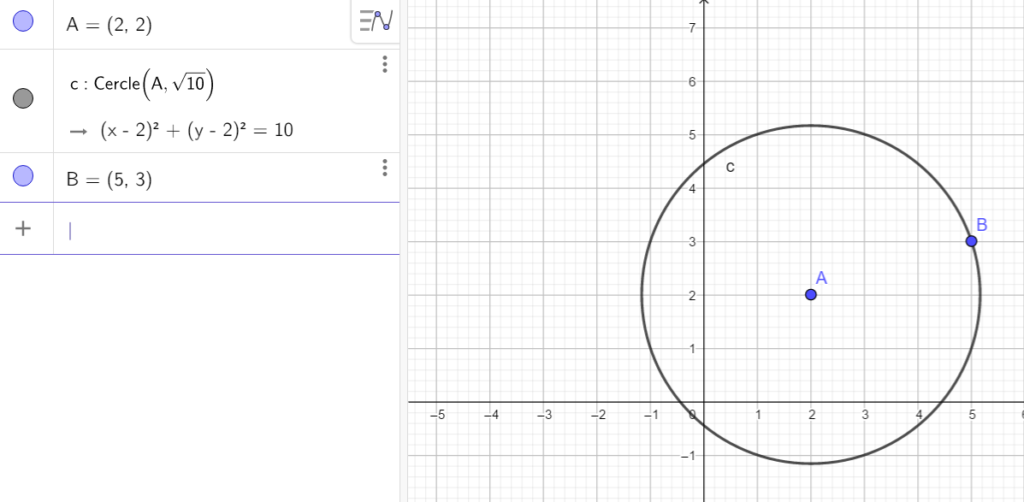
2. Vérifier que le point B(5;3) est situé sur le cercle C.

Pour placer le point B, saisir dans la colonne de gauche B=(5,3).

correction

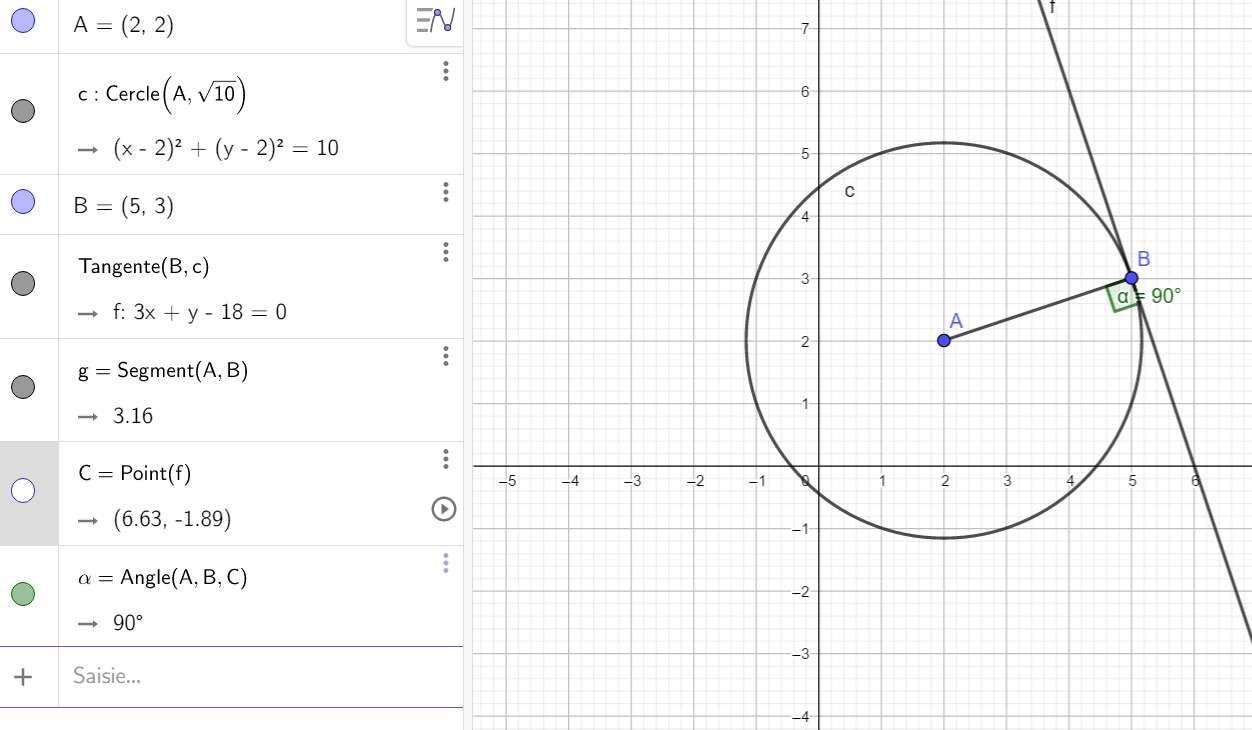
3.a) Que peut-on dire de la tangente au cercle au point B et de la droite (AB) ?

Pour tracer la tangente au cercle  C au point B, cliquer sur le quatrième onglet et sélectionner tangente dans le menu déroulant. Puis dans le repère cliquer sur le cercle  C et sur le  point B.L’équation de la tangente apparaît dans la colonne de gauche.

correction

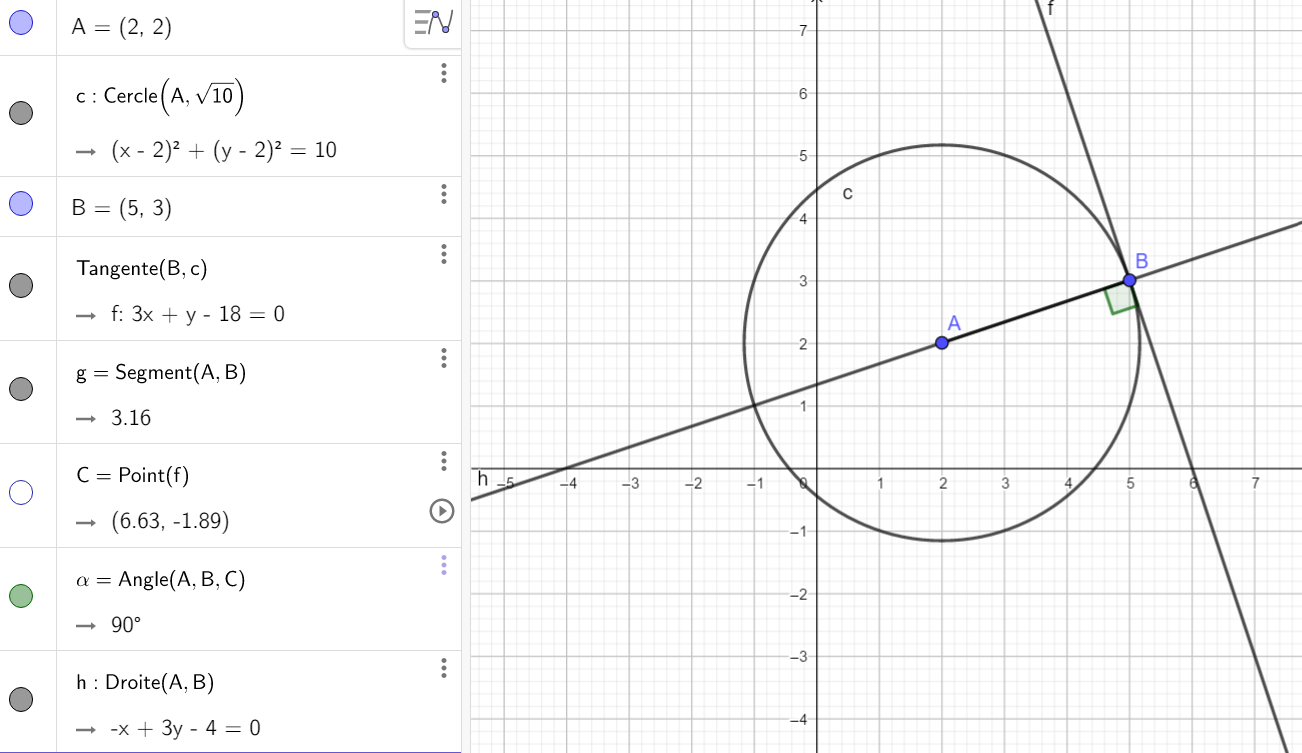
3.b) En déduire une équation cartésienne de la tangente au cercle au point B et de la droite (AB).

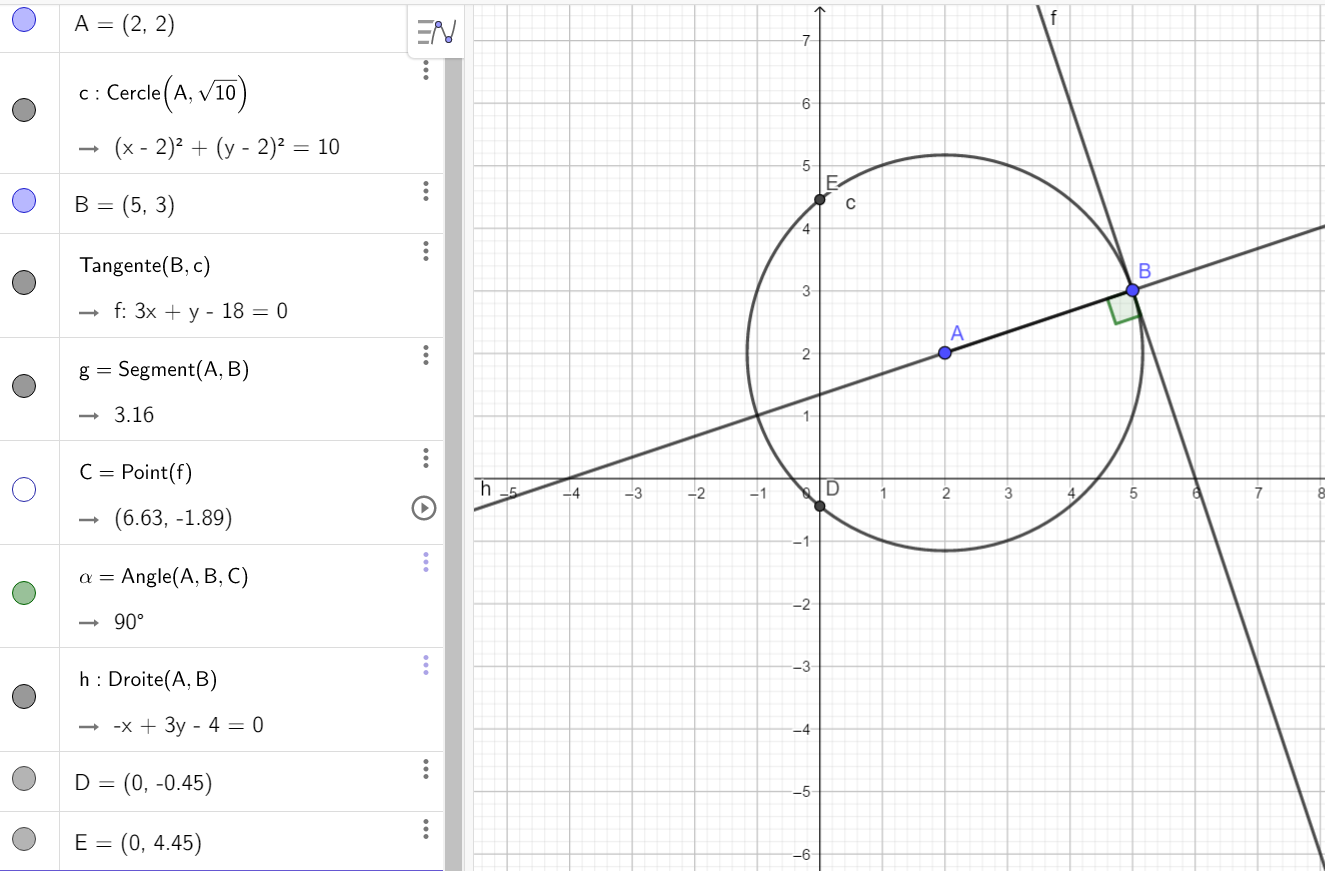
correction équation de la tangente
correction équation de (AB)

4. Calculer les coordonnées des points d’intersection du cercle C avec l’axe des ordonnées.

Pour construire les points d’intersection , cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur le cercle C et sur l’axe des ordonnées . Dans la colonne de gauche les deux points apparaissent ainsi que leurs coordonnées. On a conjecturé le résultat

correction

Exercice n°4

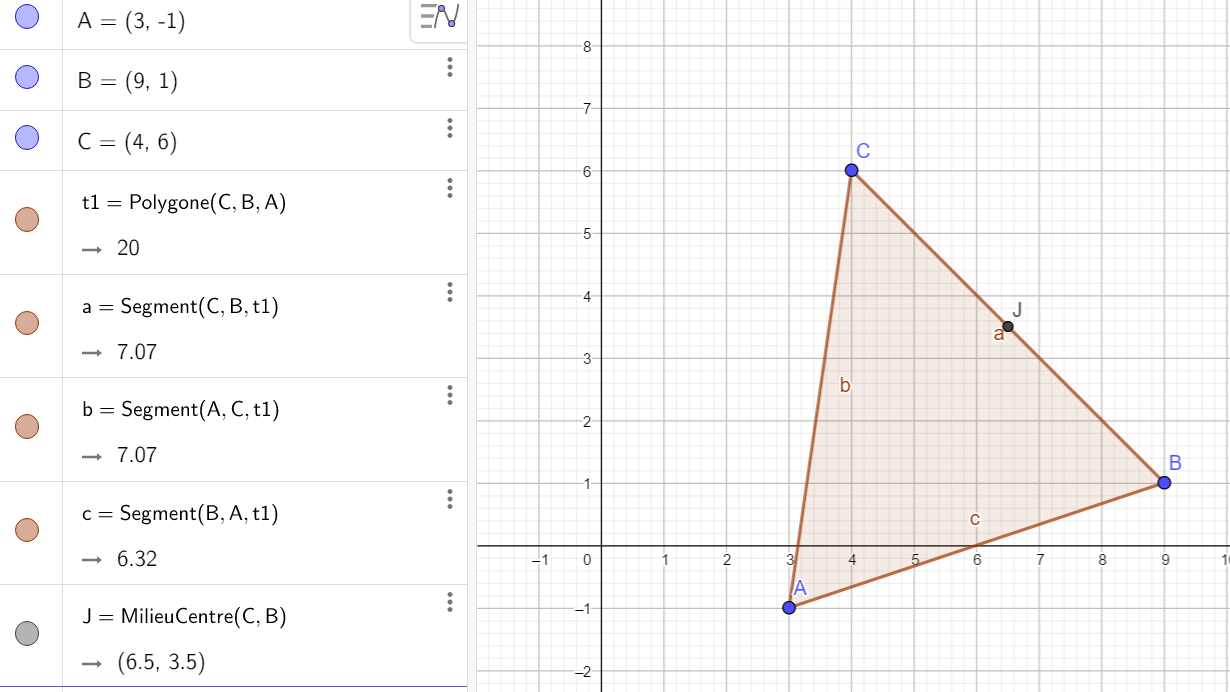
On considère les points A(3;-1), B(9;1) et C(4;6) dans un repère orthonormé.

Le but de cet exercice est de déterminer une équation cartésienne du cercle circonscrit au triangle ABC.

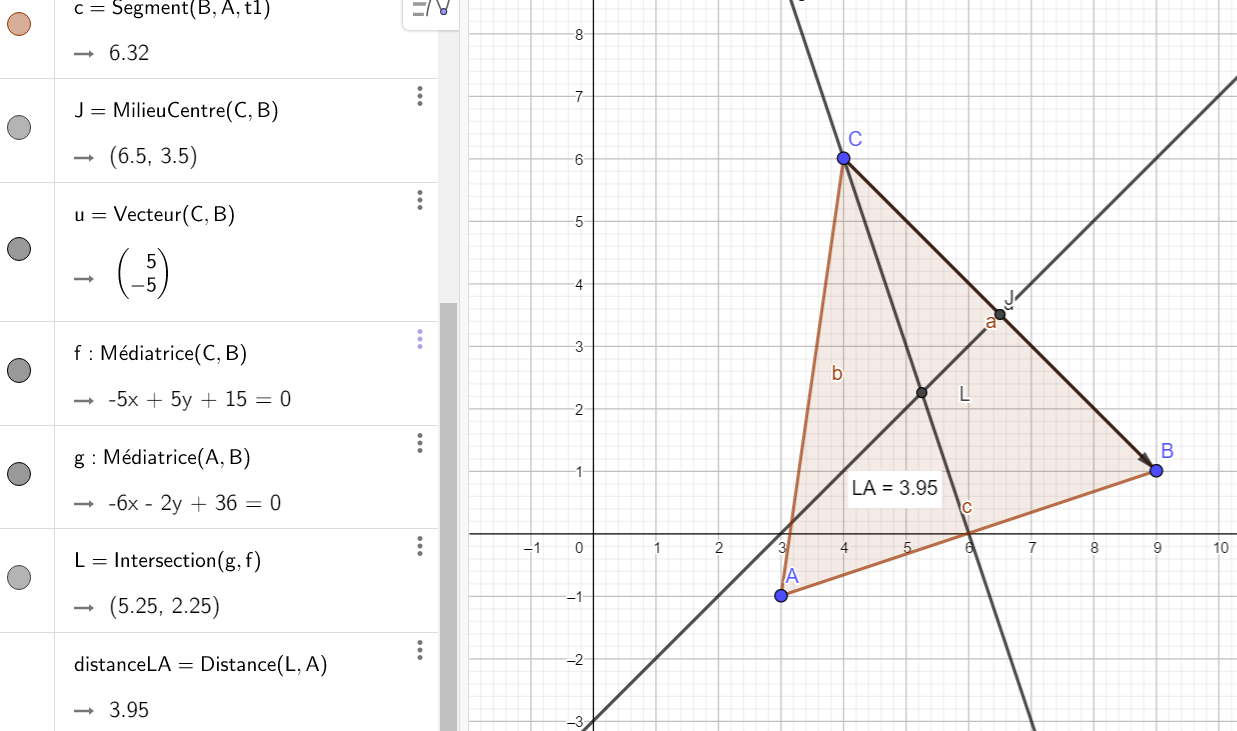
  1. a)Calculer les coordonnées de J le milieu du segment  [BC].

Pour placer J, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Milieu ou centre dans le menu déroulant et dans le repère cliquer sur le point B et sur le point  C. Dans la colonne de gauche les coordonnées de  J s’affichent. On a conjecturé le résultat.

correction

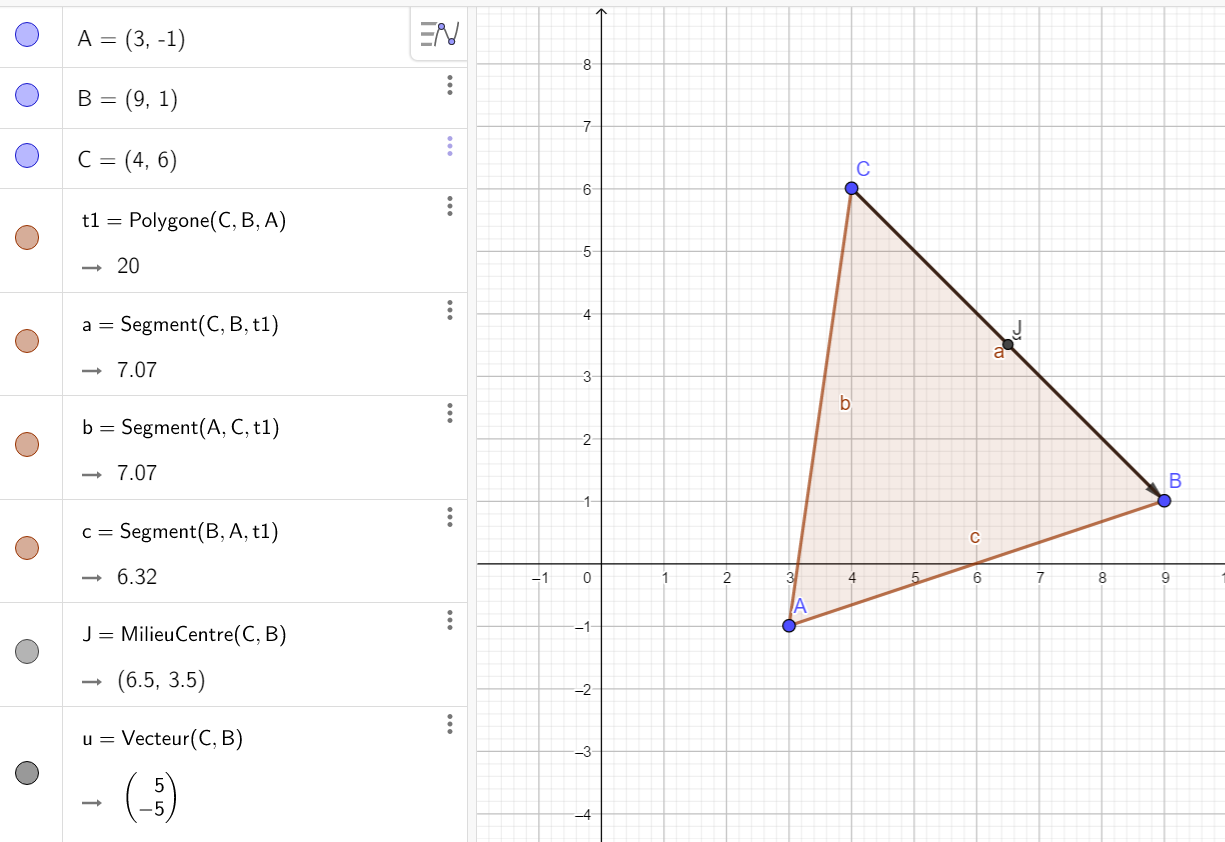
1.b)  Calculer les coordonnées du vecteur  \overrightarrow{CB}.

Pour tracer  \overrightarrow{CB}, cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Vecteur dans le menu déroulant et dans le repère cliquer sur le point C et sur le point  B. Dans la colonne de gauche les coordonnées du vecteur  \overrightarrow{CB} s’affichent. On a conjecturé le résultat.

correction

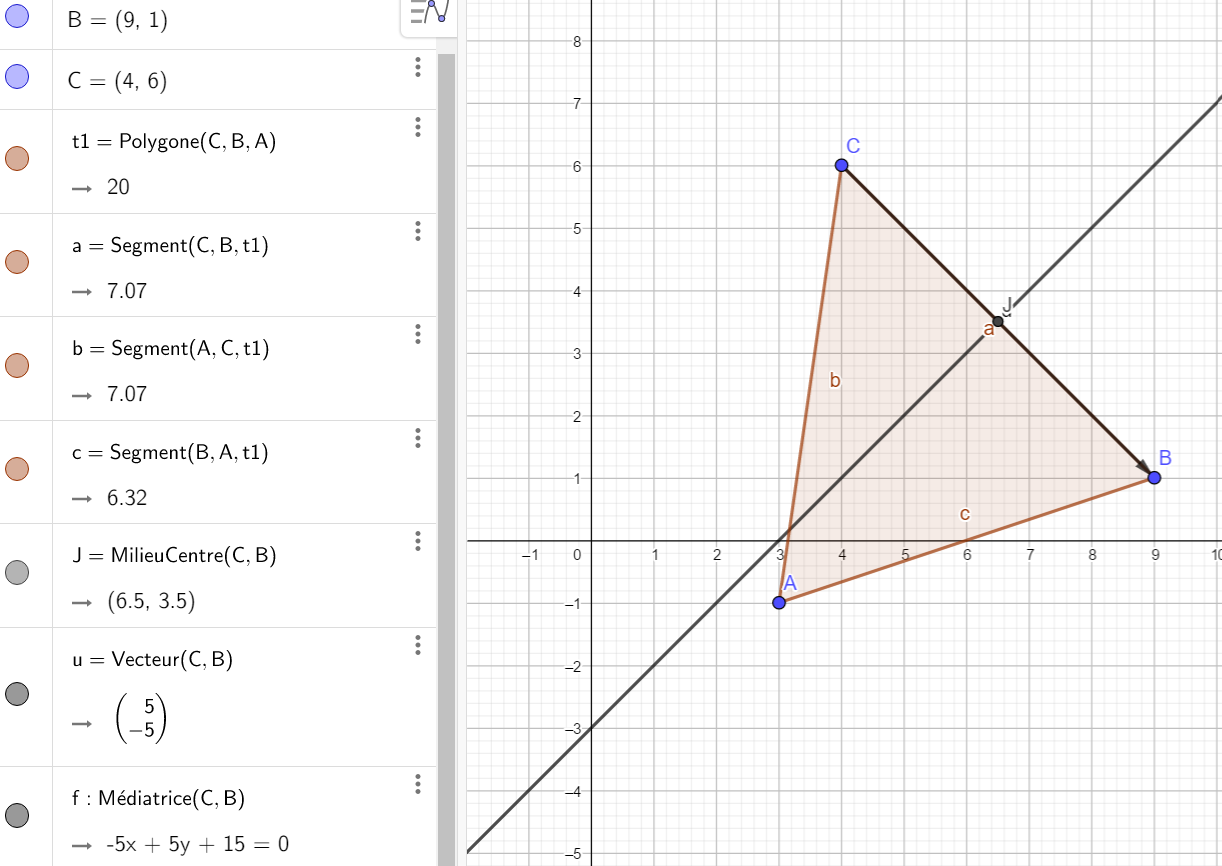
1.c)  En déduire une équation cartésienne de la médiatrice du segment  [CB].

Pour tracer la médiatrice de [CB], cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Médiatrice dans le menu déroulant et dans le repère cliquer sur le point C et sur le point  B. Dans la colonne de gauche l’équation cartésienne de la médiatrice de [CB] s’affiche. On a conjecturé le résultat.

correction

2) On admet qu’une équation de la médiatrice du segment  [AB] est -3x-y+18=0.

Pour tracer la médiatrice de [AB], cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Médiatrice dans le menu déroulant et dans le repère cliquer sur le point A et sur le point  B. Dans la colonne de gauche l’équation cartésienne de la médiatrice de [AB] s’affiche. 

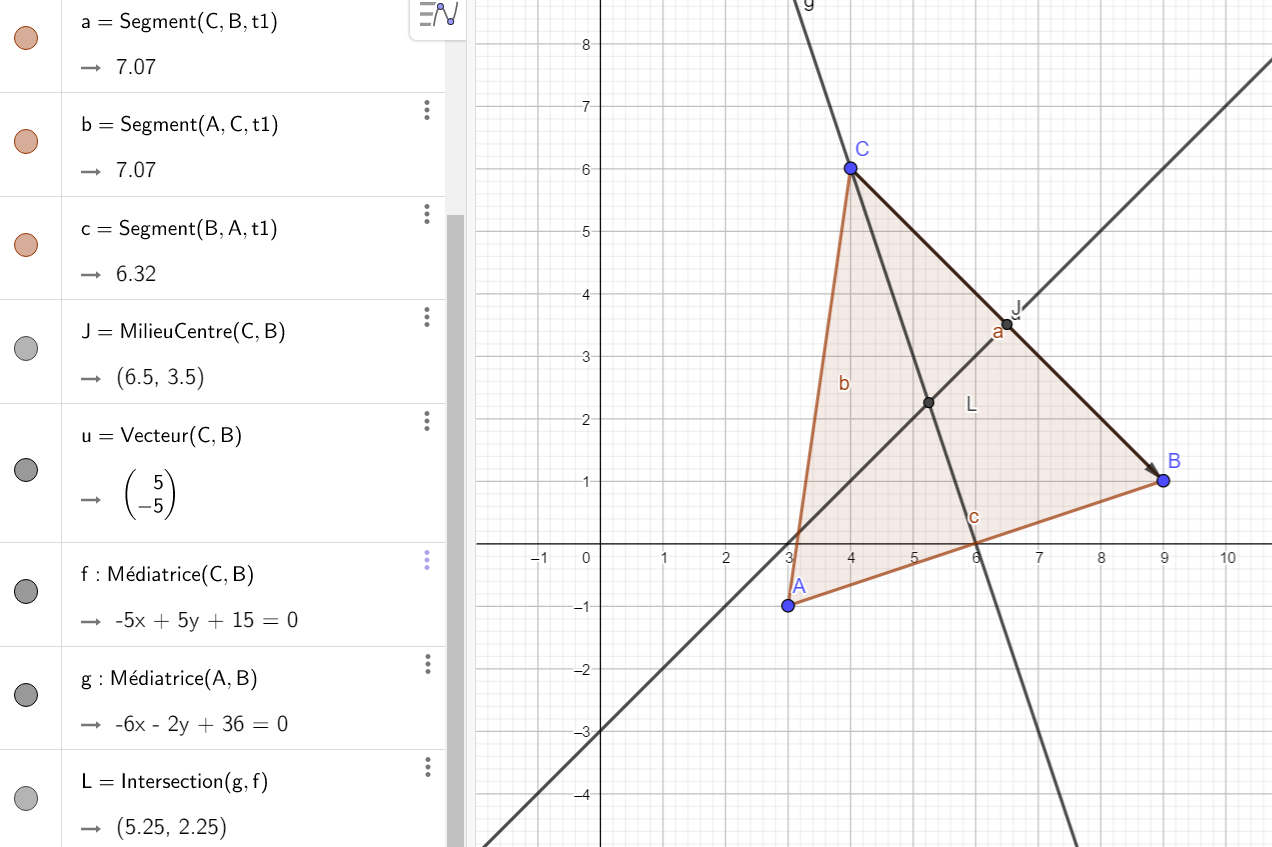
a) Déterminer par le calcul les coordonnées du point d’intersection des deux médiatrices qu’on appelera  L.

Pour construire le point d’intersection , cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur les deux médiatrices. Renommer le point. Dans la colonne de gauche le point apparaît ainsi que ses coordonnées. On a conjecturé le résultat

correction

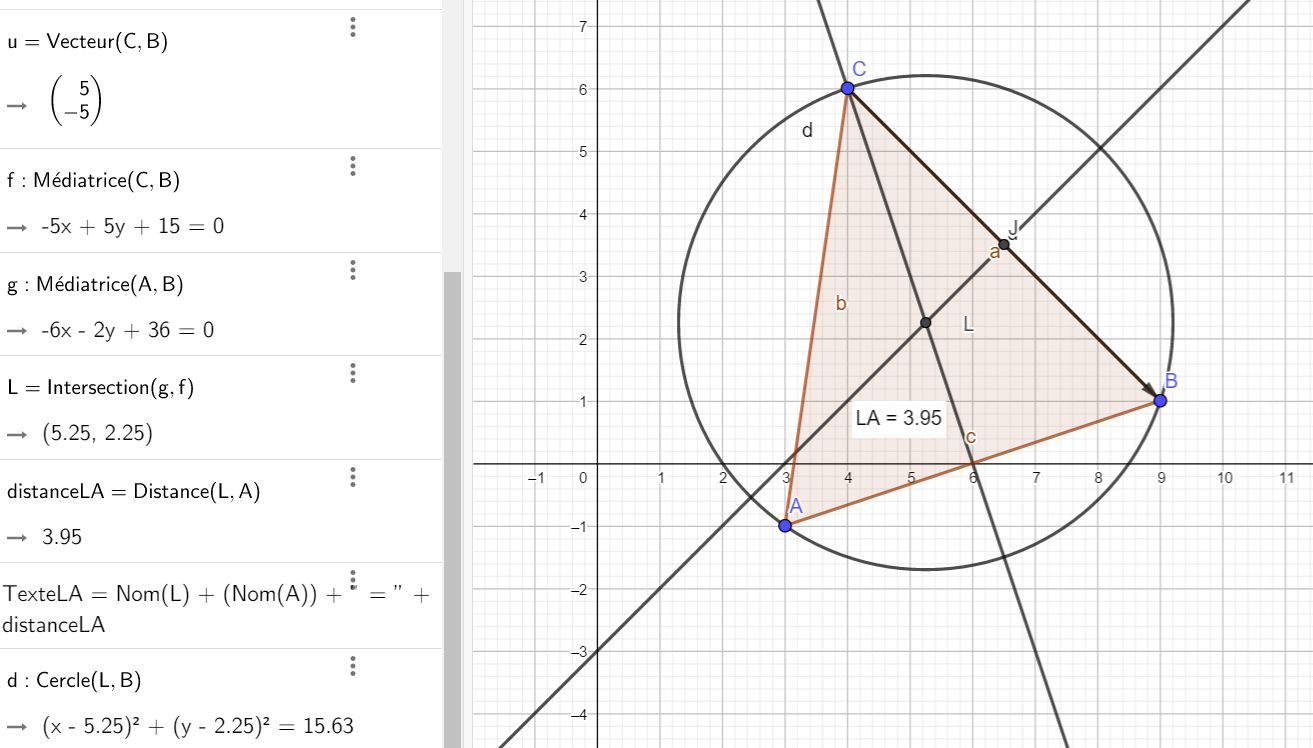
 b) Calculer la distance LA.

Pour mesurer la distance  LA, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point L et sur le point A. La distance LA s’affiche.

correction

c) En déduire une équation cartésienne du cercle circonscrit au triangle  ABC. 

Pour tracer le cercle C , cliquer sur le 6ème onglet en haut à partir de la gauche, sélectionner Cercle (centre-point) dans le menu déroulant et dans le repère cliquer sur le point L et sur le point A. Dans la colonne de gauche l’équation du cercle s’affiche. On a conjecturé le résultat.

correction

©2020 – Math’O karé SAS

Le point B a pour abscisse 6 mais son ordonnée est inconnue, on la note y_B. Donc B(6;y_B).

Le point B(6;y_B) est sur la droite d donc ses coordonnées vérifient l’équation cartésienne x-2y+4=0.

Ainsi :

On remplace x et y par 6 et y_B dans l’équation x-2y+4=0.

6-2y_B+4=0\\10-2y_B=0\\-2y_B=-10\\y_B=\frac{-10}{-2}\\y_B=5

Donc B a pour coordonnées (6;5).

 

On cherche les coordonnées d’un vecteur normal à la droite d.

La droite d’équation ax+by+c=0 admet pour vecteur normal \overrightarrow{n}(a;b).

d a pour équation x-2y+4=0 donc a=1 et b=-2.

Ainsi d aura pour vecteur normal \overrightarrow{n}(1;-2)

 

Dans la colonne de gauche, l’équation s’affiche.

On conjecture une équation de la perpendiculaire à (d) passant par A, c’est 2x+y-7=0.

On veut déterminer une équation cartésienne de \Delta la droite perpendiculaire à d qui passe par A.

On a déterminé précédemment les coordonnées du vecteur \overrightarrow{n}(1;-2) un vecteur normal à d qui du coup est un vecteur directeur de \Delta.

On utilise le résultat du cours suivant : 

On sait , d’après le cours , que le  vecteur de coordonnées (-b;a) est un vecteur directeur de la droite D d’équation ax+by+c=0 .

Donc ici  -b=1 et  a=-2.

Ou encore b=-1 et  a=-2.

Donc une équation cartésienne de \Delta est de la forme -2x-y+c=0.

Pour déterminer c, il suffit de remplacer x et y par les coordonnées du point A c’est-à-dire 3 et 1.

{-2}\times{3}-1+c=0

On résout l’équation dont l’inconnue est c.

-6-1+c=0\\-7+c=0\\c=7

Une équation de la droite \Deltaest -2x-y+7=0.

Remarque avec Géogébra, on obtient 2x+y-7=0. Il s’agit bien sûr de la même droite  D qui possède plusieurs équations cartésiennes qui se déduisent toutes les unes des autres en multipliant par un nombre ici -1. 

 

Le point H est situé sur les deux droites donc ses coordonnées (x;y) vérifient les deux équations x-2y+4=0 et 2x+y-7=0.

Il faut résoudre le système suivant :

On va le résoudre par le calcul et par combinaison linéaire.

Je décide d’éliminer les y , pour cela je dois multiplier la deuxième équation par 2.

Ainsi on aura -2y dans la première équation et son opposé 2y  dans la nouvelle deuxième équation.

ATTENTION : quand on dit que je dois multiplier la deuxième  équation par  2 , je multiplie tout par 2   .

J’ajoute membre à membre ces deux égalités (les y disparaissent, ce qui était le but recherché)

x+4x+4-14=0\\5x-10=0\\5x=10\\x=\frac{10}{5}\\x=2

Pour déterminer la valeur de y  je remplace x par 2  dans par exemple la première équation.

2-2y+4=0

6-2y=0

-2y=-6

y=\frac{-6}{-2}

y=3

Donc le point H a pour coordonnées (2;3)

 

On n’hésite pas à repérer les coordonnées des points A et H ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.6cm} x_{H} y_{H}

\hspace{0.2cm} A(3;1) \hspace{0.4cm} H(2;3)

On écrit la formule du cours :

AH=\sqrt {{(x_H-x_A) }^{2}+{(y_H-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AH=\sqrt {{(2-3)}^{2}+{(3-1)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AH=\sqrt {{(-1)}^{2}+{2}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AH=\sqrt {1+4}

On effectue ensuite la somme

AH=\sqrt {5}

Cette distance est la distance entre le point A et la droite (d).

 

Voici la figure obtenue avec Géogébra, on conjecture que le milieu I a pour coordonnées (2.5;2.5).

On n’hésite pas à repérer les coordonnées des points A et C ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.8cm} x_{C} y_{C}

\hspace{0.2cm} A(-5;1) \hspace{0.4cm} C(10;4)

On écrit la formule du cours :

Le milieu I de [AC] a pour coordonnées :(\frac {x_A+x_C}{2};\frac {y_A+y_C}{2})

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

Le milieu I de [AC] a pour coordonnées : (\frac {(-5)+10}{2};\frac {1+4}{2})

Le milieu I de [AC] a pour coordonnées : (\frac {5}{2};\frac {5}{2})

Donc I(\frac {5}{2};\frac {5}{2})

 

Voici la figure obtenue avec Géogébra, on conjecture que le vecteur \overrightarrow{AC} a pour coordonnées (15;3).

Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}

\hspace{1.8cm}A(-5;1)\hspace{2cm}C(10;4)

J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(10-(-5);4-1)

\overrightarrow{AC}(10+5;3)

\overrightarrow{AC}(15;3)

 

Voici la médiatrice obtenue avec Géogébra, on conjecture qu’une équation cartésienne est

-15x-3y+45=0.

On veut déterminer une équation cartésienne de la médiatrice du segment [AC].

Reformulons la question. On veut déterminer une équation cartésienne de la droite perpendiculaire à (AC) passant par I le milieu de [AC].

On utilise le résultat du cours suivant : Une droite  d de vecteur normal  \overrightarrow{n}(a;b) a une équation cartésienne de la forme ax+by+c=0 où c est un nombre réel.

On a calculé les coordonnées du vecteur \overrightarrow{AC} qui est normal à la médiatrice de [AC].

\overrightarrow{AC}(15;3)

On remplace a par 15 et b par 3 dans l’équation  ax+by+c=0.

Une équation cartésienne de la médiatrice de [AC] est de la forme :

15x+3y+c=0

Pour déterminer c, il faut remplacer x et y par les coordonnées d’un point de la droite et résoudre l’équation dont c est l’inconnue.

La médiatrice de [AC] passe par I, le milieu de [AC].

On a déjà calculé les coordonnées de I.

I(\frac{5}{2}; \frac{5}{2})

On remplace x par \frac {5}{2} et  y par \frac {5}{2} dans 15x+3y+c=0.

15\times \frac {5}{2}+3\times \frac {5}{2}+c=0

\frac {75}{2}+\frac {15}{2}+c=0

\frac {90}{2}+c=0

45+c=0

c=-45

Une équation cartésienne de la médiatrice de [AC] est 15x+3y-45=0

Géogébra donne une autre équation cartésienne -15x-3y+45=0 qui se déduit de la précédente en multipliant par -1, c’est donc la même droite.

 

Voici la figure géogébra, on conjecture qu’une équation cartésienne de la médiatrice du segment [BC] est -11x+3y+33=0.

On donne B(-1;7) et C(10;4).

On veut déterminer une équation cartésienne de la médiatrice du segment [BC].

On choisit d’appeler J le milieu de [BC].

Reformulons la question. On veut déterminer une équation cartésienne de la droite perpendiculaire à (BC) passant par J le milieu de [BC].

On utilise le résultat du cours suivant : Une droite  d de vecteur normal  \overrightarrow{n}(a;b) a une équation cartésienne de la forme ax+by+c=0 où c est un nombre réel.

On va calculer les coordonnées du vecteur \overrightarrow{BC} qui est normal à la médiatrice de [BC].

Je repère les coordonnées des points B et C.

\hspace{2.1cm}x_{B}\hspace{0.2cm}y_{B}\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}

\hspace{1.8cm}B(-1;7)\hspace{2cm}C(10;4)

J’écris la formule : \overrightarrow{BC}(x_{C}-x_{B};y_{C}-y_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BC}(10-(-1);4-7)

\overrightarrow{BC}(10+1;-3)

\overrightarrow{BC}(11;-3)

On remplace a par 11 et b par -3 dans l’équation  ax+by+c=0.

Une équation cartésienne de la médiatrice de [BC] est de la forme :

11x-3y+c=0

Pour déterminer c, il faut remplacer x et y par les coordonnées d’un point de la droite et résoudre l’équation dont c est l’inconnue.

La médiatrice de [BC] passe par J, le milieu de [BC].

Calculons les coordonnées de J.

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.4cm} x_{B} y_{B} \hspace{0.8cm} x_{C} y_{C}

\hspace{0.2cm} B(-1;7) \hspace{0.4cm} C(10;4)

On écrit la formule du cours :

Le milieu J de [BC] a pour coordonnées :(\frac {x_B+x_C}{2};\frac {y_B+y_C}{2})

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

Le milieu J de [BC] a pour coordonnées : (\frac {(-1)+10}{2};\frac {7+4}{2})

Le milieu J de [BC] a pour coordonnées : (\frac {9}{2};\frac {11}{2})

Donc J(\frac {9}{2};\frac {11}{2})

On remplace x par \frac {9}{2} et  y par \frac {11}{2} dans 11x-3y+c=0.

11\times \frac {9}{2}-3\times \frac {11}{2}+c=0

\frac {99}{2}- \frac {33}{2}+c=0

\frac {66}{2}+c=0

33+c=0

c=-33

Une équation cartésienne de la médiatrice de [BC] est 11x-3y-33=0

 

 

Voici la figure Géogébra, on conjecture que le point \Omega a pour coordonnées (3;0).

Le point \Omega est situé sur les deux médiatrices donc ses coordonnées (x;y) vérifient les deux équations 15x+3y-45=0 et 11x-3y-33=0.

Il faut résoudre le système suivant :

On va le résoudre par le calcul et par combinaison linéaire.

Je décide d’éliminer les y , pour cela j’ajoute membre à membre les deux égalités.

15x+3y-45+11x-3y-33=0\\26x-78=0\\26x=78\\x=\frac{78}{26}\\x=3

Pour déterminer la valeur de y  je remplace x par 3  dans par exemple la première équation 

15x+3y-45=0.

15\times 3+3y-45=0

45+3y-45=0

3y=0

y=\frac{0}{3}

y=0

Donc le point \Omega a pour coordonnées (3;0).

 

On n’hésite pas à repérer les coordonnées des points A et \Omega ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{\Omega} y_{\Omega}

\hspace{0.2cm} A(-5;1) \hspace{0.4cm} \Omega(3;0)

On écrit la formule du cours :

A\Omega=\sqrt {{(x_\Omega-x_A) }^{2}+{(y_\Omega-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

A\Omega=\sqrt {{(3-(-5))}^{2}+{(0-1)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

A\Omega=\sqrt {{8}^{2}+{(-1)}^{2}}

On effectue ensuite les puissances, ici les carrés. 

A\Omega=\sqrt {64+1}

On effectue ensuite la somme

A\Omega=\sqrt {65}

 

Voici la figure Géogébra, on conjecture que l’équation du cercle est (x-3)^2+y^2=65

On applique le résultat du cours :

C est un cercle de centre \Omega(x_\Omega;y_\Omega) et de rayon r.

Une équation cartésienne de C est (x-x_\Omega)^2+(y-y_\Omega)^2=r^2.

Comme \Omega(1;3) et r=\sqrt{65}

On remplace x_\Omega par 1, y_\Omega par 3 et r par 2 dans l’équation (x-x_\Omega)^2+(y-y_\Omega)^2=r^2.

Une équation cartésienne du cercle circonscrit à ABC est

(x-3)^2+(y-0)^2=\sqrt{65}^2

c’est-à-dire (x-3)^2+(y-0)^2=65

 

Voici la figure géogébra, on conjecture le résultat : (x-2)^2+(y-2)^2=10

On applique le résultat du cours :

C est un cercle de centre A(x_A;y_A) et de rayon r.

Une équation cartésienne de C est (x-x_A)^2+(y-y_A)^2=r^2.

Comme A(2;2) et r=\sqrt{10}

On remplace x_A par 2, y_A par 2 et r par \sqrt{10} dans l’équation (x-x_A)^2+(y-y_A)^2=r^2.

Une équation cartésienne de C est

(x-2)^2+(y-2)^2=\sqrt{10}^2

c’est-à-dire (x-2)^2+(y-2)^2=10.

 

Voici la figure géogébra, en plaçant le point B, il semble être sur le cercle.

Une équation cartésienne de C est

(x-2)^2+(y-2)^2=10.

Remplacer x par l’abscisse de B c’est-à-dire 5 et y par l’ordonnée de B c’est-à-dire 3 dans (x-2)^2+(y-2)^2, calculer et montrer que le résultat vaut 10.

(x_B-2)^2+(y_B-2)^2=(5-2)^2+(3-2)^2

\hspace{3.4cm}=3^2+1^2

\hspace{3.4cm}=9+1

\hspace{3.4cm}=10

Les coordonnées vérifient l’équation cartésienne du cercle donc B appartient au cercle C.

 

Voici la figure géogébra, en traçant la tangente, on voit bien qu’elle est perpendiculaire au rayon.

La tangente à  C au point  B est par définition perpendiculaire au rayon.

Ainsi la tangente à  C au point  B est  perpendiculaire à la droite (AB).

 

A l’aide de Géogébra, on conjecture que l’équation de la tangente est 3x+y-18=0

On veut déterminer une équation cartésienne de  la tangente à C en B.

On utilise le résultat du cours suivant : Une droite  d de vecteur normal  \overrightarrow{n}(a;b) a une équation cartésienne de la forme ax+by+c=0 où c est un nombre réel.

On va calculer les coordonnées du vecteur \overrightarrow{AB} qui est normal à la tangente. 

Je repère les coordonnées des points A et B.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}A(2;2)\hspace{2cm}B(5;3)

J’écris la formule : \overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(5-2;3-2)

\overrightarrow{AB}(3;1)

On remplace a par 3 et b par 1 dans l’équation  ax+by+c=0.

Une équation cartésienne de la tangente est de la forme :

3x+1\times y+c=0

3x+y+c=0

Pour déterminer c, il faut remplacer x et y par les coordonnées d’un point de la droite et résoudre l’équation dont c est l’inconnue.

La tangente passe par B(5;3), on remplace x par 5 et  y par 3 dans 3x+y+c=0.

3\times 5+3+c=0

15+3+c=0

18+c=0

c=-18

Une équation cartésienne de la tangente est 3x+y-18=0.

 

A l’aide de géogébra, on conjecture une équation cartésienne de (AB) : -x+3y-4=0. Elle est en bas de la colonne de gauche.

Déterminer par le calcul une équation cartésienne de la  droite (AB) qui passe par  A (2;2) et B (5;3) .

On a vu précédemment que \overrightarrow{AB} (3;1) 

Le vecteur \overrightarrow{AB} (3;1) est un vecteur directeur de (AB) .

On sait , d’après le cours , que le  vecteur de coordonnées (-b;a) est un vecteur directeur de la droite D d’équation ax+by+c=0 .

Donc ici  -b=3 et  a=1.

Ou encore b=-3 et  a=1.

Donc l’équation cartésienne de D est de la forme x-3y+c=0.

Pour déterminer c, il suffit de remplacer x et y par les coordonnées du point A c’est-à-dire 2 et 2.

2-{3}\times{2}+c=0

On résout l’équation dont l’inconnue est c.

2-6+c=0\\-4+c=0\\c=4

Une équation cartésienne de la droite (AB) est x-3y+4=0.

 

A l’aide de la fenêtre Géogébra, on conjecture les coordonnées des deux points d’intersection. Le logiciel les a appelé D et E et leurs coordonnées apparaissent en bas de la colonne à gauche D(0.-0.45) et E(0;4.45) .

Les points cherchés appartiennent au cercle donc leurs coordonnées (x;y) vérifient l’équation cartésienne (x-2)^2+(y-2)^2=10.

Les points cherchés appartiennent à l’axe des ordonnées donc leurs coordonnées (x;y) vérifient l’équation cartésienne x=0.

On remplace x par 0 dans l’équation (x-2)^2+(y-2)^2=10 et on résout l’équation dont l’inconnue est y.

(0-2)^2+(y-2)^2=10\\4+(y-2)^2=10\\(y-2)^2=10-4\\(y-2)^2=6\\(y-2)^2=\sqrt{6}^2

Les carrés de deux nombres sont égaux si les nombres sont égaux ou s’ils sont opposés.

y-2=\sqrt{6}  ou  y-2=-\sqrt{6}\\y=\sqrt{6}+2  ou  y=-\sqrt{6}+2.

Les coordonnées des points d’intersection sont (0;\sqrt{6}+2) et (0;-\sqrt{6}+2).

 

Voici la figure Géogébra, on conjecture que J(6.5;3.5).

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.4cm} x_{B} y_{B} \hspace{0.8cm} x_{C} y_{C}

\hspace{0.2cm} B(9;1) \hspace{0.4cm} C(4;6)

On écrit la formule du cours :

Le milieu J de [BC] a pour coordonnées :(\frac {x_B+x_C}{2};\frac {y_B+y_C}{2})

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

Le milieu J de [BC] a pour coordonnées : (\frac {9+4}{2};\frac {1+6}{2})

Le milieu J de [BC] a pour coordonnées : (\frac {13}{2};\frac {7}{2})

Donc J(\frac {13}{2};\frac {7}{2})

 

Voici la figure Géogébra, on conjecture que \overrightarrow{CB}(5;-5).

Pour déterminer les coordonnées du vecteur \overrightarrow{CB}.

Je repère les coordonnées des points C et B.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}C(4;6)\hspace{2cm}B(9;1))

J’écris la formule : \overrightarrow{CB}(x_{B}-x_{C};y_{B}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CB}(9-4;1-6)

\overrightarrow{CB}(5;-5)

 

Voici la figure Géogébra, on conjecture qu’une équation cartésienne de la médiatrice de  (BC) est  -5x+5y+15=0.

On donne B(9;1) et C(4;6).

On veut déterminer une équation cartésienne de la médiatrice du segment [BC].

Reformulons la question. On veut déterminer une équation cartésienne de la droite perpendiculaire à (BC) passant par J le milieu de [BC].

On utilise le résultat du cours suivant : Une droite  d de vecteur normal  \overrightarrow{n}(a;b) a une équation cartésienne de la forme ax+by+c=0 où c est un nombre réel.

Les coordonnées du vecteur \overrightarrow{BC} qui est normal à la médiatrice de [BC] sont (5;-5) .

On remplace a par [latex5[/latex] et b par -5 dans l’équation  ax+by+c=0.

Une équation cartésienne de la médiatrice de [BC] est de la forme :

5x-5y+c=0

Pour déterminer c, il faut remplacer x et y par les coordonnées d’un point de la droite et résoudre l’équation dont c est l’inconnue.

La médiatrice de [BC] passe par J, le milieu de [BC].

Les coordonnées de J sont (\frac{13}{2};\frac{7}{2}).

On remplace x par \frac {13}{2} et  y par \frac {7}{2} dans 5x-5y+c=0.

5\times \frac {13}{2}-5\times \frac {7}{2}+c=0

\frac {65}{2}- \frac {35}{2}+c=0

\frac {30}{2}+c=0

15+c=0

c=-15

Une équation cartésienne de la médiatrice de [BC] est 5x-5y-15=0

Géogébra donne pour équation -5x+5y+15=0. Si on multiplie par -1 on obtient la même équation donc c’est la même droite.

 

Voici la figure Géogébra, on conjecture que L, le point d’intersection de deux médiatrices a pour coordonnées  (5.25;2.25).

Le point L est situé sur les deux médiatrices donc ses coordonnées (x;y) vérifient les deux équations 5x-5y-15=0 et -3x-y+18=0.

Il faut résoudre le système suivant :

On va le résoudre par le calcul et par combinaison linéaire.

Je décide d’éliminer les y , pour cela je multiplie la deuxième équation par (-5).

J’ajoute membre à membre ces deux égalités.

5x-5y-15+15x+5y-90=0\\20x-105=0\\20x=105\\x=\frac{105}{20}\\x=\frac{21}{4}

Pour déterminer la valeur de y  je remplace x par \frac{21}{4}  dans par exemple la première équation 

5x-5y-15=0.

5\times \frac{21}{4}-5y-15=0

\frac{105}{4}-5y-15\times \frac{4}{4}=0

\frac{105}{4}-5y- \frac{60}{4}=0

\frac{45}{4}-5y=0

-5y=-\frac{45}{4}

y=\frac{-\frac{45}{4}}{-5}

y=\frac{45}{4}\times \frac{1}{5}

y=\frac{9}{4}

Donc le point L a pour coordonnées (\frac{21}{4};\frac{9}{4}).

 

Voici la figure Géogébra, on conjecture que la distance  LA mesure 3.95.

On n’hésite pas à repérer les coordonnées des points A et L ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{L} y_{L}

\hspace{0.2cm} A(3;-1) \hspace{0.4cm} L(\frac{21}{4};\frac{9}{4})

On écrit la formule du cours :

AL=\sqrt {{(x_L-x_A) }^{2}+{(y_L-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AL=\sqrt {{(\frac{21}{4}-3)}^{2}+{(\frac{9}{4}-(-1))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AL=\sqrt {{(\frac{21}{4}-3\times \frac{4}{4})}^{2}+{(\frac{9}{4}+1\times \frac{4}{4})}^{2}}\\AL=\sqrt {{(\frac{21}{4}-\frac{12}{4})}^{2}+{(\frac{9}{4}+\frac{4}{4})}^{2}}\\AL=\sqrt {{(\frac{9}{4})}^{2}+{(\frac{13}{4})}^{2}}

On effectue ensuite les puissances, ici les carrés. 

AL=\sqrt {\frac{81}{16}+\frac{169}{16}}

On effectue ensuite la somme

AL=\sqrt {\frac{250}{16}}

AL= \frac{\sqrt{250}}{\sqrt {16}}

AL= \frac{\sqrt{25}\times \sqrt{10} }{\sqrt {16}}

AL= \frac{5\sqrt{10} }{4}

Géogébra donne pour résultat 3.95 qui est une valeur approchée de \frac{5\sqrt{10} }{4}.

 

Voici la figure Géogébra, on conjecture qu’une équation cartésienne du cercle de centre L passant  parA est (x-5.25)^2+(y-2.25)^2=15.63.

On applique le résultat du cours :

C est le cercle circonscrit au triangle ABC, il a pour centre L(x_L;y_L) et de rayon AL.

Une équation cartésienne de C est (x-x_L)^2+(y-y_L)^2=AL^2.

Comme L(\frac{21}{4};\frac{9}{4}) et AL=\frac{5\sqrt{10}}{4}

On remplace x_L par \frac{21}{4}, y_L par \frac{9}{4} et AL par \frac{5\sqrt{10}}{4} dans l’équation (x-x_L)^2+(y-y_L)^2=AL^2.

Une équation cartésienne de C est

(x-\frac{21}{4})^2+(y-\frac{9}{4})^2=(\frac{5\sqrt{10}}{4})^2

c’est-à-dire

(x-\frac{21}{4})^2+(y-\frac{9}{4})^2=\frac{250}{16}

Géogébra donne le résultat suivant : (x-5.25)^2+(y-2.25)^2=15.63. Ce qui est cohérent car 15.63 est une valeur approchée de \frac{250}{16}.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.