Exercice n°1
Soit la suite (u_n) définie par , u_0=2 et u_{n+1}=0.2u_n+2
a) u_3=2.6 | b) u_3=2.48 | c) u_3=2.496 | d) u_3=2.4 |
Exercice n°2
Soit (u_n) une suite arithmétique de raison r que u_6=19 et u_9=10
a) r=-9 | b) r=\frac{10}{19} | c) r=3 | d) r=-3 |
Exercice n°3
Soit (u_n) une suite arithmétique de raison r=0.4 que u_{10}=24. Quelle est la valeur de u_2 ?
a) 20 | b) 6.8 | c) 20.8 | d) 0.8 |
Exercice n°4
Soit (u_n) une suite arithmétique de raison r=2 et de premier terme u_0=3. Quelle est la valeur de la somme des 12 premiers termes, S=u_0+u_1+…+u_{11} ?
a) 154 | b) 14 | c) 36 | d) 168 |
Exercice n°5
Soit (u_n) une suite de premier terme u_0=10 et vérifiant u_{n+1}=u_n+\frac{20}{100}u_n . Quelle est la nature de la suite (u_n) ?
a) géométrique de raison \frac{20}{100} | b) géométrique de raison 1 | c) arithmétique de raison \frac{20}{100} | d) géométrique de raison 1.2 |
Exercice n°6
La somme 4+5+6+…+9999+1000 est égale
a) 500500 | b) 500494 | c) 502000 | d) 499900 |
Exercice n°7
Voici une fonction Python :
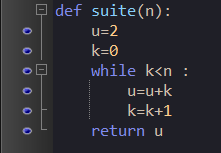
Quelle valeur est renvoyée si on tape suite(5) dans la console ?
a) 5 | b) 8 | c) 12 | d) 17 |
Exercice n°8
La somme 1+3+3^2+…+3^{10} est égale
a) 324775 | b) 88573 | c) 177147 | d) 29524 |
Exercice n°9
Soit (u_n) une suite de premier terme u_0=2 et vérifiant u_{n+1}=u_n+n+1 . Quelle affirmation est exacte ?
a) u_1=4 | b) (u_n) est arithmétique de raison 1 | c) (u_n) est décroissante | d) u_2=6 |
Exercice n°10
La somme 1+2+2^2+…+2^{20} est égale
a) 21\times\frac{1+2^{20}}{2} | b) \frac{2^{20}-1}{2} | c) \frac{1-2^{20}}{2} | d) 2^{21}-1 |
Exercice n°11
Soit (u_n) une suite de premier terme u_0=1 et vérifiant u_{n+1}=2\times u_n+1 .
On veut déterminer la plus petite valeur de n telle que (u_n) est supérieur ou égal à 10 000. On réalise pour cela le programme incomplet ci-dessous écrit en langage Python :
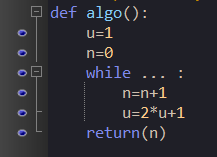
Pour que l’algorithme renvoie la valeur demandée, il faut compléter les pointillés par :
a) u==10000 | b) u=10000 | c) u<10000 | d) u>10000 |



