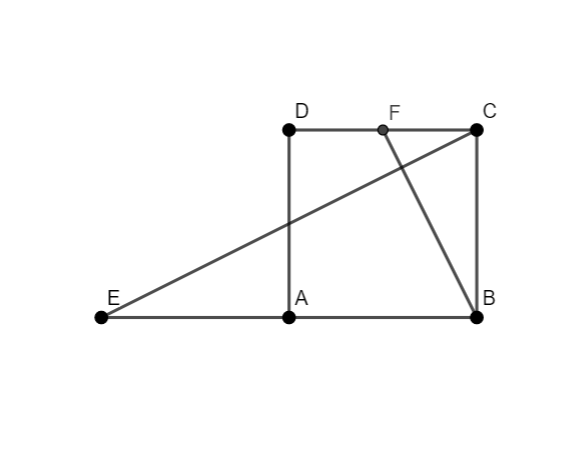
ABCD est un carré.
F est le milieu du segment [DC].
E est le symétrique du point B par rapport à A.
On veut montrer que les droites (BF) et (CE) sont perpendiculaires.
L’idée est d’utiliser un repère pour étudier la position des deux droites.
On choisit le repère (A,\overrightarrow{AB},\overrightarrow{AD}).
On lit graphiquement les coordonnées des points de la figure.
A(0;0). C’est l’origine du repère.
B(1;0). Il se trouve sur l’axe des abscisses.
D(0;1). Il se trouve sur l’axe des ordonnées.
C(1;1) car ABCD est un carré.
E(-1;0) car A est le milieu de [EB].
F(0.5;1) car F est le milieu de [DC].
On va calculer les coordonnées des vecteurs \overrightarrow{BF} et \overrightarrow{CE}. Puis on va montrer que le produit scalaire \overrightarrow{BF}.\overrightarrow{CE} est nul en utilisant la forme analytique du produit scalaire.
- Calcul des coordonnées du vecteur \overrightarrow{BF}.
Pour déterminer les coordonnées du vecteur \overrightarrow{BF}.
Je repère les coordonnées des points B et F.
\hspace{2.1cm}x_{B}\hspace{0.2cm}y_{B}\hspace{2cm}x_{F}\hspace{0.2cm}y_{F}
\hspace{1.8cm}B(1;0)\hspace{2cm}F(0.5;1)
J’écris la formule : \overrightarrow{BF}(x_{F}-x_{B};y_{F}-y_{B})
On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.
\overrightarrow{BF}(0.5-1;1-0)
\overrightarrow{BF}(-0.5;1)
2. Calcul des coordonnées du vecteur \overrightarrow{CE}.
Pour déterminer les coordonnées du vecteur \overrightarrow{CE}.
Je repère les coordonnées des points C et E.
\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{2cm}x_{E}\hspace{0.2cm}y_{E}
\hspace{1.8cm}C(1;1)\hspace{2cm}E(-1;0)
J’écris la formule : \overrightarrow{CE}(x_{E}-x_{C};y_{E}-y_{C})
On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.
\overrightarrow{CE}((-1)-1;0-1)
\overrightarrow{CE}(-2;-1)
3. Calcul du produit scalaire \overrightarrow{BF}.\overrightarrow{CE}
On utilise la forme analytique \overrightarrow{u}.\overrightarrow{v}=xx’+yy’.
On a montré que \overrightarrow{BF}(-0.5;1) et que \overrightarrow{CE}(-2;-1).
On remplace x par -0.5 , y par 1 , x’ par -2 et y’ par -1 dans xx’+yy’.
\overrightarrow{BF}.\overrightarrow{CE}=(-0.5)\times (-2)+1\times(-1)
\hspace{1.3cm}=1-1
\hspace{1.3cm}=0
Leur produit scalaire est nul donc les vecteurs \overrightarrow{BF} et \overrightarrow{CE} sont donc orthogonaux.
Donc les droites (BF) et (CE) sont perpendiculaires.



