Actuellement le taux de mortalité des abeilles est de 30 % par an en moyenne en France.
Un apiculteur possède 200 colonies et compte-tenu du taux de mortalité, il décide de rajouter 42 colonies chaque année pour essayer de stabiliser sa production.
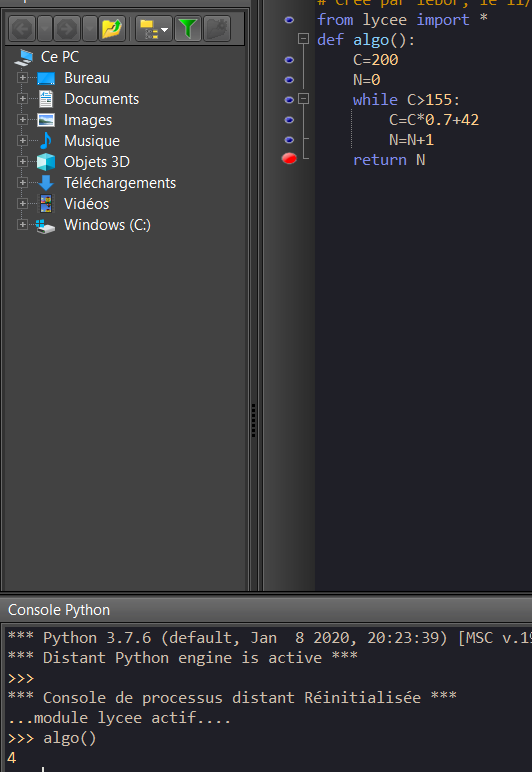
- On donne le programme suivant écrit en langage Python :

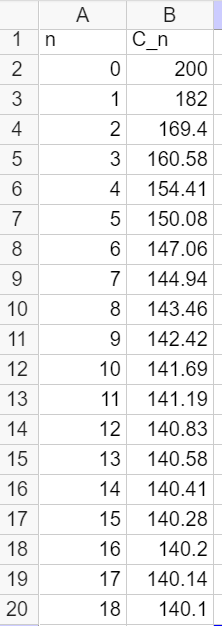
a. Faire tourner le programme à la main et compléter le tableau ci-dessous ( arrondir les valeurs C à l’unité près )

b. Quelle est la valeur de N renvoyée par le programme ? Interpréter ce résultat dans le contexte de l’exercice.
On note C_n le nombre de colonies d’abeilles au début de la nième année .
On a alors C_0=200.
On admet que pour tout entier n,
C_{n+1}=0.7C_n+42.
2. La suite C_n est-elle arithmétique ? La suite C_n est-elle géométrique ?
3. On admet que C_n=60\times 0.7^n+140. L’apiculteur pourra-t-il espérer atteindre les 150 colonies dans le futur ? Vous pourrez utiliser la page géogébra ci-dessous en saisissant la bonne formule dans la cellule B2.
4. Calculer lim_{n\to +\infty}C_n. Interpréter le résultat dans le cadre de l’exercice.