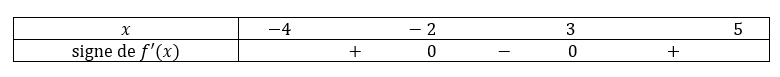logo

T.Continuité, théorème des valeurs intermédiaires

Sommaire

Continuité d’une fonction

Définition : Une fonction f est continue sur un intervalle I si la courbe de f est obtenue sans jamais lever le crayon de la feuille.

Le trait est obtenu sans lever le crayon, la fonction carré est continue sur l’intervalle [-2;2] 

Le trait est obtenu en levant le crayon le crayon, la fonction inverse n’est pas continue sur l’intervalle [-2;2] 

Propriété : Une fonction f dérivable sur un intervalle I est continue sur l’intervalle I .

Théorème des valeurs intermédiaires.

Théorème :

Une fonction f est continue sur un intervalle I.

a et b désignent deux réels de I tels que a<b

Pour tout réel k compris entre f(a) et f(b) il existe au moins un réel c compris entre a et b tel que f(c)=k.

Illustration graphique du théorème

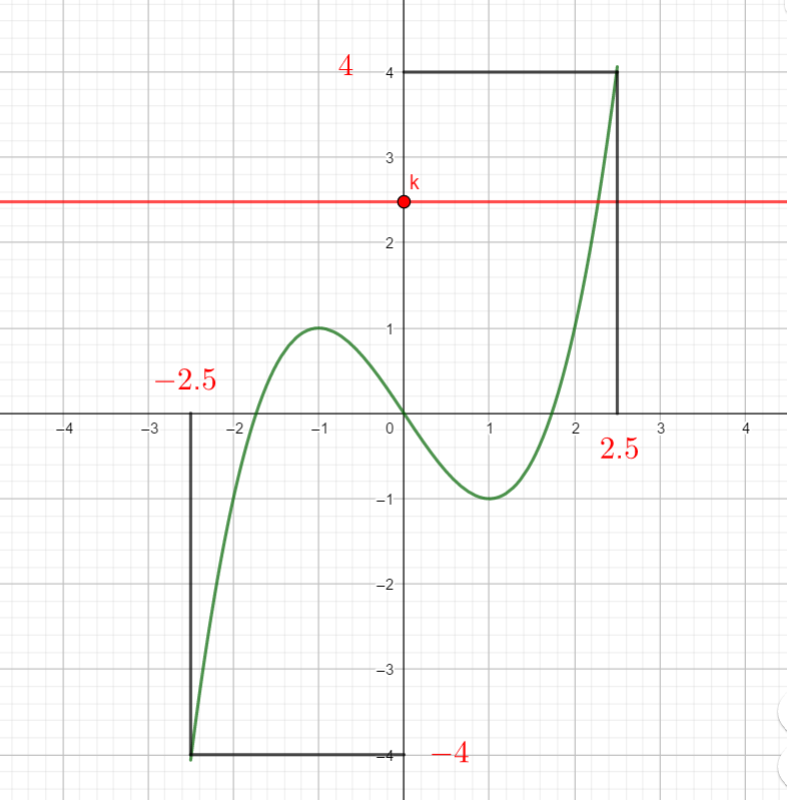
Dans la fenêtre Géogébra ci-dessous, f(x)=\frac{x^3-3x}{2} , a=-2.5 et b=2.5.

  1. Déterminer graphiquement f(a) et f(b) c’est-à-dire f(-2.5) et f(2.5)
correction

2. En déplacant le k du graphique, déterminer une valeur de k pour laquelle f(c)=k admet 

a. une solution

correction

b. deux solutions

correction

c. trois solutions

correction

Propriété

On considère une fonction f définie, continue et strictement monotone ( c’est-à-dire strictement croissante ou strictement décroissante )sur un intervalle [a;b].

Pour tout réel k compris entre  f(a) et f(b) l’équation f(x)=k admet une unique solution ( souvent notée \alpha ) dans l’intervalle [a;b].

Remarque : cette propriété peut être étendue à tout type d’intervalle.

Illustration graphique de la propriété 

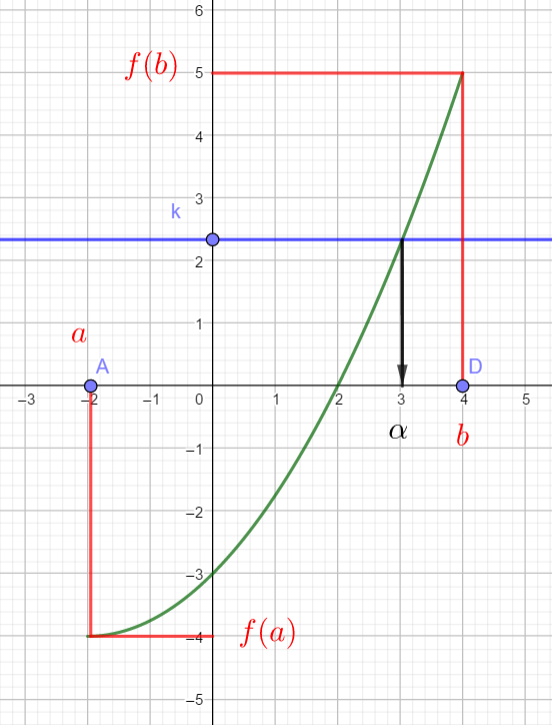
Cas d’une fonction strictement croissante

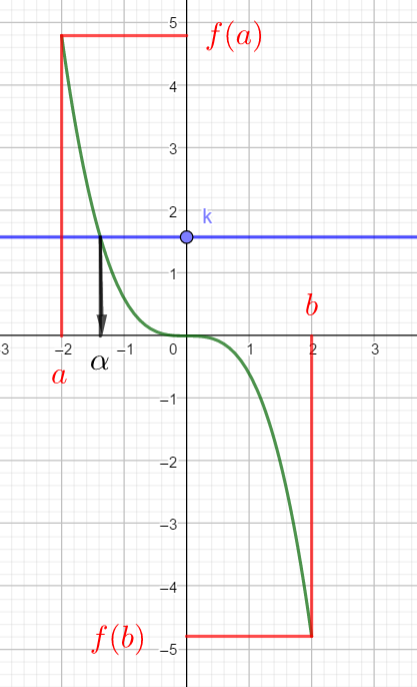
Cas d’une fonction strictement décroissante

Illustration  de la propriété avec un tableau de variations

Exercices 

Exercice n°1 

AIDE : Dans cet exercice et les suivants, il faudra calculer f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.

CALCUL FORMEL GEOGEBRA: calcul de f'(x)

De plus il faudra étudier le signe de f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.

CALCUL FORMEL GEOGEBRA: signe de f'(x)

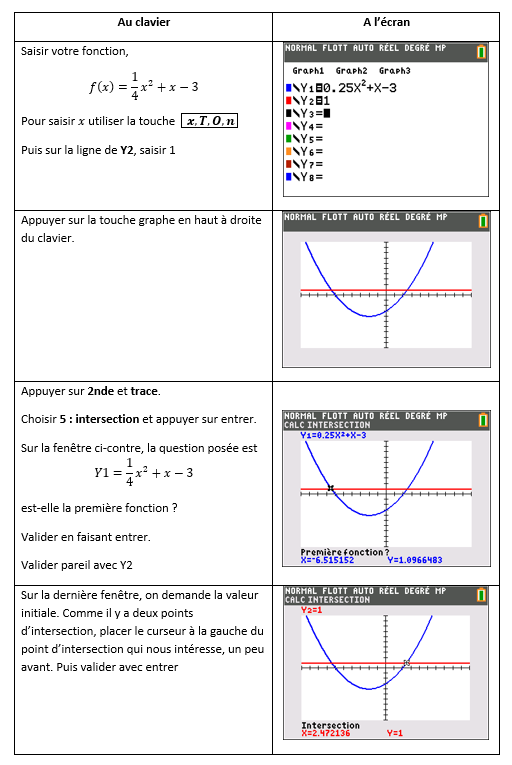
Soit la fonction f définie sur [-2;4] par f(x)=\frac{1}{4}x^2+x-3.

  1. Calculer f'(x).
correction

2. Etudier le signe de f'(x) sur [-2;4].

correction

3. Dresser le tableau de la fonction f sur l’intervalle [-2;4].

correction

4.a. Démontrer que l’équation  f(x)=1 sur admet une solution unique notée \alpha dans l’intervalle [-2;4].

correction

4.b. A l’aide de la calculatrice, déterminer une valeur approchée de  \alpha à 10^{-2} près.

correction

Exercice n°2 

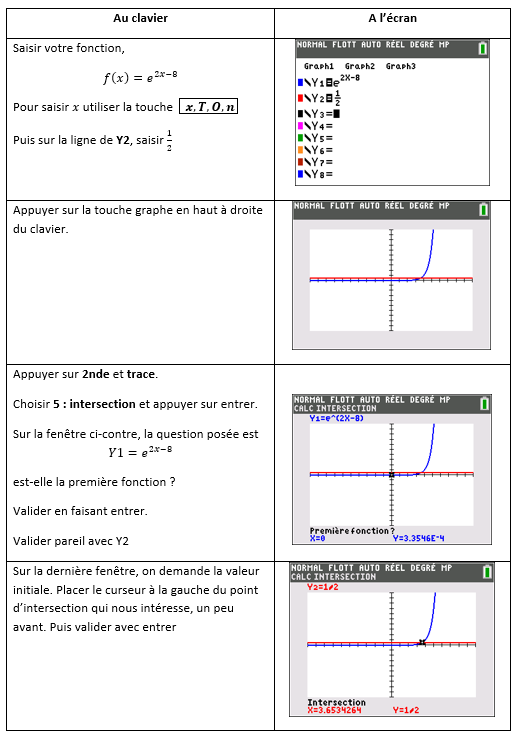
Soit la fonction f définie sur [0;4] par f(x)=e^{2x-8}.

  1. Calculer f'(x).
correction

2. Etudier le signe de f'(x) sur [0;4].

correction

3. Dresser le tableau de la fonction f sur l’intervalle [0;4].

correction

4.a. Démontrer que l’équation  f(x)=\frac{1}{2} sur admet une solution unique notée \alpha dans l’intervalle [0;4].

correction

4.b. A l’aide de la calculatrice, déterminer une valeur approchée de  \alpha à 10^{-2} près.

correction

Exercice n°3 

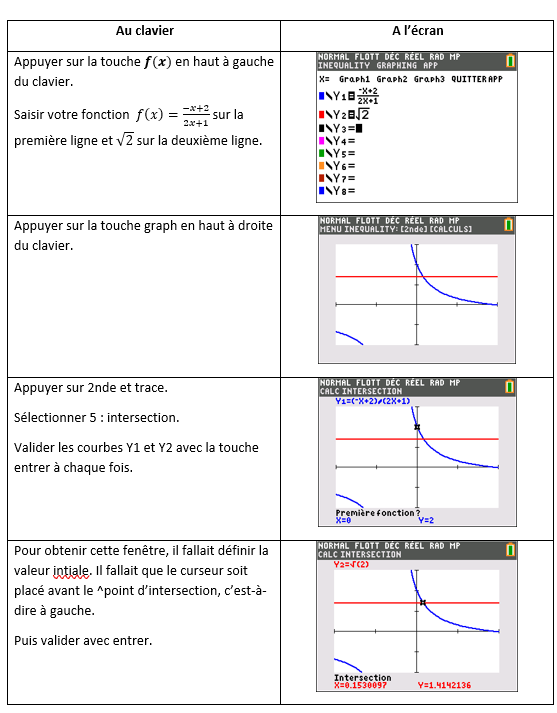
Soit la fonction f définie sur [0;10] par f(x)=\frac{-x+2}{2x+1}.

  1. Calculer f'(x).
correction

2. Etudier le signe de f'(x) sur [0;10].

correction

3. Dresser le tableau de la fonction f sur l’intervalle [0;10].

correction

4.a. Démontrer que l’équation  f(x)=\sqrt{2} sur admet une solution unique notée \alpha dans l’intervalle [0;10].

correction

4.b. A l’aide de la calculatrice, déterminer la valeur de \alpha .

correction

Exercice n°4 

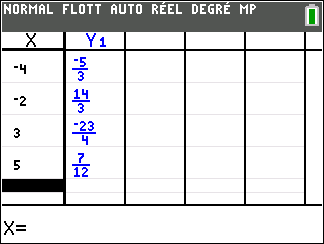
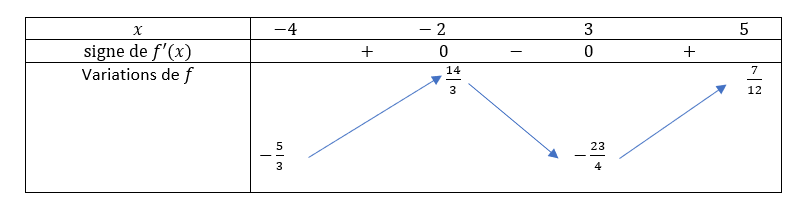
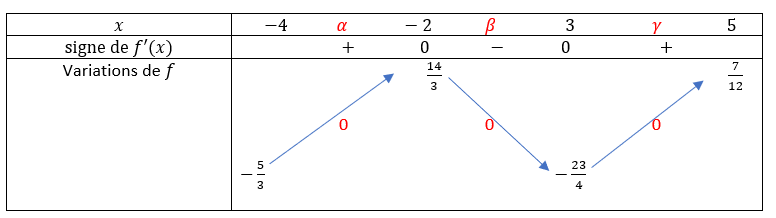
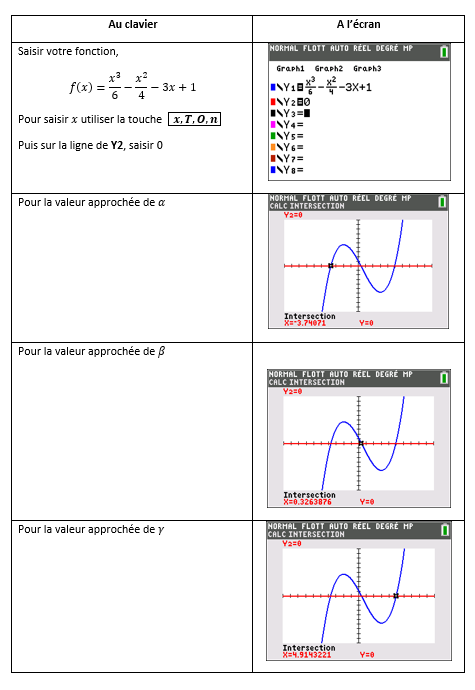
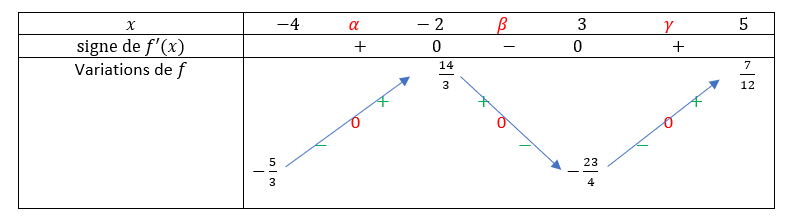
Soit la fonction f définie sur [-4;5] par f(x)=\frac{x^3}{6}-\frac{x^2}{4}-3x+1.

  1. Calculer f'(x).
correction

2. Etudier le signe de f'(x) sur [-4;5].

correction

3. Dresser le tableau de la fonction f sur l’intervalle [-4;5].

correction

4.a. Démontrer que l’équation  f(x)=0  admet trois solutions notées \alpha,\beta,\gamma dans l’intervalle [-4;5].

correction

4.b. A l’aide de la calculatrice, déterminer une valeur approchée pour chaque solution à 10^{-2} près.

correction

5. En déduire le signe de la fonction f sur l’intervalle [-4;5].

correction

Valider les variations avec Géogébra

On saisit par exemple f(x)=\frac{1}{4}x^2+x-3 la fonction de l’exercice n°1 dans la colonne de gauche et on lit graphiquement les variations de f  sur [-2;4] puis on compare avec le tableau de variations obtenu.

©2020 – Math’O karé SAS

Pour  déterminer les images de -2.5 et de 2.5, procéder comme ci-dessous.

les images de -2.5 et de 2.5 sont -4 et 4.

 

 

Pour toutes les valeurs de k  telles que -4\leq k<-1 ou 1< k\leq4, k ne possède qu’un seul antécédent c tel que f(c)=k.

Réponses possibles : –3; -2; 2; 3……

Lorsque k=-1 ou  k=1 , k  possède exactement deux antécédents.

Pour toutes les valeurs de k  telles que -1<k<1 , k possède trois antécédents c tel que f(c)=k.

Réponses possibles : -0.9; 0; 0.5; 1.75……

Vérification du calcul de la dérivée f'(x) avec Géogébra.

Sur la ligne 1, saisir l’expression de la fonction f(x)=

Ensuite cliquer sur l’onglet f’.

Apparaît ensuite dans la fenêtre Dérivée: f'(x)= le résultat.

Vérification du signe de la dérivée f'(x) avec Géogébra.

Un exemple : soit f(x)=x^3-3x.

On calcule f'(x)=3x^2-3

Sur la ligne 1, saisir l’inégalité obtenue en écrivant l’expression de f'(x) suivie de par exemple, >0 c’est-à-dire

3x^2-3>0. 

En écrivant cette inégalité, on cherche pour quelles valeurs de x   , la dérivée f'(x) est positive.

Ensuite cliquer sur l’onglet X=.

Apparaît ensuite dans la fenêtre Résoudre:  le résultat ( c’est-à-dire les valeurs de x pour lesquelles la dérivée est positive).

Pour l’exemple, on obtient

Résoudre {x<-1,x>1}

Soit la fonction f définie sur [-2;4] par f(x)=\frac{1}{4}x^2+x-3

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de trois termes :

\frac{1}{4}x^2 , x et -3.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

Il faut donc calculer les dérivées des trois termes \frac{1}{4}x^2 , x et -3. en utilisant le tableau n°2 ci-dessous

(\frac{1}{4}x^2)’=\frac{1}{4}(x^2)’ d’après la 2ème formule du tableau n°1 et (x^2)’=2x d’après la 3ème formule du tableau n°2.

Donc (\frac{1}{4}x^2)’=\frac{1}{4}\times 2x=\frac{1}{2}x

(x)’=1  d’après la 2ème formule du tableau n°2.

(-3)’=0 d’après la 1ème formule du tableau n°2.

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{1}{4}x^2+x-3)’\\f'(x)= (\frac{1}{4}x^2)’+(x)’-(3)’\\f'(x)= \frac{1}{4}(x^2)’+(x)’-(3)’\\f'(x)= \frac{1}{4}\times 2x+1+0\\f'(x)= \frac{1}{2}x+1

 

 

On veut étudier le signe de f'(x)=\frac{1}{2}x+1.

On utilise la deuxième ligne du tableau ci-dessous : la quantité est de la forme ax+b.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On fait un tableau de signes comme en seconde.

On fait un tableau de signes comme en seconde.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

On résout l’inéquation quantité > 0 et on détermine pour quelles valeurs de x la quantité est positive. On déduit ensuite les valeurs de x pour lesquelles la quantité est négative

a=\frac{1}{2}  donc le signe de a est positif .

b=1\\-\frac{b}{a}=-\frac{1}{\frac{1}{2}}=-2

On en déduit le tableau de signes suivant

On utilise la question précédente pour remplir la ligne du signe de f'(x).

On calcule  f(-2) et f(4) pour compléter la troisième ligne.

f(-2)=\frac{1}{4}\times (-2)^2+(-2)-3=-4

f(4)=\frac{1}{4}\times 4^2+4-3=5

 

 

On veut montrer que l’équation f(x)=1 admet une unique solution notée \alpha sur l’intervalle [-2;4]

Pour bien visualiser la situation, on peut placer \alpha sur la ligne des x et 1 sur la ligne des f(x) dans le tableau de variations comme ci-dessous.

la fonction f est  continue et  strictement croissante sur l’intervalle [-2;4].

Comme  1\in[-4;5] alors l’équation f(x)=1 admet une unique solution notée \alpha sur l’intervalle [-2;4].

 

Pour déterminer à la calculatrice TI 83 Premium CE une valeur approchée de  \alpha.

On cherche l’abscisse du point d’intersection de la courbe de f(x)=\frac{1}{4}x^2+x-3 et de y=1 sur l’intervalle [-2;4] en procédant comme ci-dessous.

Une valeur approchée de \alpha à 10^{-2} près est 2.47.

 

f(x)= e^{2x-8} pour x\in [0;4]

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction , le quotient de deux fonctions  , le carré d’une fonction ou e^{u(x)}  ? (la liste s’allonge)

C’est de la forme  e^{u(x)} avec  u(x)=2x-8.

D’après le cours : La fonction e^u:x\rightarrow e^{u(x)} est dérivable et (e^u)'(x)= u'(x) \times {e^{u(x)}} 

Calcul de u'(x)

u(x) est une somme

u'(x)=(2x-8)’

u'(x)=(2x)’-(8)’

u'(x)=2\times(x)’-(8)’

u'(x)=2\times1-0

u'(x)=2-0

u'(x)=2

Calcul de f'(x)

On calcule en remplaçant u(x) par 2x-8 et u'(x) par 2 dans la formule u'(x) \times {e^{u(x)}}  .

Voici ce qu’il faut écrire sur la copie :

f'(x)=(e^{2x-8})’

f'(x)=(2x-8)’ e^{2x-8}

f'(x)=2e^{2x-8}

 

Nous avons trouvé précédemment f'(x)=2e^{2x-8}.

D’après les résultats du cours , e^x>0 pour tout x \in\mathbf{R}.

Donc f'(x)>0 pour x \in[0;4]

On utilise la question précédente pour remplir la ligne du signe de f'(x).

On calcule  f(0) et f(4) pour compléter la troisième ligne.

f(0)=e^{2\times 0-8}=e^{-8}

f(4)=e^{2\times 4-8}=e^{8-8}=e^0=1

 

 

On veut montrer que l’équation f(x)=\frac{1}{2} admet une unique solution notée \alpha sur l’intervalle [0;4]

Pour bien visualiser la situation, on peut placer \alpha sur la ligne des x et \frac{1}{2} sur la ligne des f(x) dans le tableau de variations comme ci-dessous.

la fonction f est  continue et  strictement croissante sur l’intervalle [0;4].

Comme  \frac{1}{2}\in[e^{-8};1] alors l’équation f(x)=\frac{1}{2} admet une unique solution notée \alpha sur l’intervalle [0;4].

Pour déterminer à la calculatrice TI 83 Premium CE une valeur approchée de  \alpha.

On cherche l’abscisse du point d’intersection de la courbe de f(x)=e^{2x-8} et de y=\frac{1}{2} sur l’intervalle [0;4] en procédant comme ci-dessous.

Une valeur approchée de \alpha à 10^{-2} près est 3.65.

 

 

 f(x)= \frac{-x+2}{2x+1} pour x\in [0;10] 

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=-x+2 et v(x)=2x+1.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

2a.on veut calculer la dérivée  u'(x)

u(x)=-x+2 est une est une somme, on utilise la 1ère ligne du tableau n°1 

u'(x)=(-x+2)’

u'(x)=(-x)’+(2)’

On utilise la ligne 2 du tableau 1 pour remplacer (-x)’ par -(x)’ 

u'(x)=-(x)’+(2)’

On utilise les lignes 1 et 2 du tableau 2 ci-dessous pour finir le calcul.

u'(x)=-1+0

u'(x)=-1

2b.on veut calculer la dérivée  v'(x)

v(x)=2x+1 est une somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(2x+1)’

v'(x)=(2x)’+(1)’

v'(x)=2(x)’+(1)’

On utilise les lignes 1 et 2 du tableau 2 ci-dessous pour finir le calcul.

v'(x)=2\times 1+0

v'(x)=2

3. On calcule la dérivée f'(x) 

On remplace u par  -x+2,  v par 2x+1, u’ par  -1 et v’ par 2 dans la formule \frac{u’\times v-u\times v’}{v^2} 

 Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{-x+2}{2x+1})’\\f'(x)=\frac{(-x+2)’\times{(2x+1)}-{(-x+2)}\times{(2x+1)’}}{(2x+1)^2}\\f'(x)=\frac{(-1)\times{(2x+1)}-{(-x+2)}\times{2}}{(2x+1)^2}

On développe les deux produits au numérateur. Petit conseil, pour éviter les erreurs de signe laisser le deuxième développement entre parenthèses.

f'(x)=\frac{(-2x-1)-(-2x+4)}{(2x+1)^2}

Enlever les parenthèses. Attention il y a un signe moins devant, on change le signe de ce qu’il y a entre parenthèses.

f'(x)=\frac{-2x-1+2x-4}{(2x+1)^2} 

On réduit au numérateur

f'(x)=\frac{-5}{(2x+1)^2} 

 

On veut étudier le signe de f'(x)=\frac{-5}{(2x+1)^2}.

On utilise la septième ligne du tableau ci-dessous : la quantité est un quotient.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On étudie le signe de chaque facteur et on fait un tableau de signes comme en seconde.

On étudie le signe du numérateur et le signe du dénominateur. Si nécessaire, ensuite on fait un tableau de signes comme en seconde.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

Comme le dénominateur (2x+1)^2 est un carré, il est positif.

Le quotient est donc du signe du numérateur : -5.

Donc f'(x) est de signe négatif.

 

 

 

 

On utilise la question précédente pour remplir la ligne du signe de f'(x).

On calcule f(0) et f(10) pour compléter la troisième ligne.

f(0)=\frac{-0+2}{2\times0+1}=\frac{2}{1}=2

f(10)=\frac{-10+2}{2\times10+1}=-\frac{8}{21}

 

 

On veut montrer que l’équation f(x)=\sqrt{2} admet une unique solution notée \alpha sur l’intervalle [0;10]

Pour bien visualiser la situation, on peut placer \alpha sur la ligne des x et \sqrt{2} sur la ligne des f(x) dans le tableau de variations comme ci-dessous.

la fonction f est  continue et  strictement décroissante sur l’intervalle [0;10].

Comme  \sqrt{2}\in[-\frac{8}{21};2] alors l’équation f(x)=\sqrt{2} admet une unique solution notée \alpha sur l’intervalle [0;10].

Pour déterminer à la calculatrice TI 83 Premium CE une valeur approchée de  \alpha.

On cherche l’abscisse du point d’intersection de la courbe de f(x)=\frac{-x+2}{2x+1} et de y=0 (c’est-à-dire l’axe des abscisses) sur l’intervalle [0;10] en procédant comme ci-dessous.

Une valeur approchée de \alpha à 10^{-2} près est 0.15.

Soit la fonction f définie sur [-4;5] par f(x)=\frac{x^3}{6}-\frac{x^2}{4}-3x+1.

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est une somme de quatre termes .

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

Il faut donc calculer les dérivées des quatre termes  en utilisant les deux tableaux .

(\frac{x^3}{6})’=\frac{1}{6}(x^3)’ d’après la 2ème formule du tableau n°1 

(\frac{x^3}{6})’=\frac{1}{6}\times 3x^2 d’après la 4ème formule du tableau n°2 ( avec n=3)

(\frac{x^3}{6})’=\frac{x^2}{2}

(\frac{x^2}{4})’=\frac{1}{4}(x^2)’ d’après la 2ème formule du tableau n°1 

(\frac{x^2}{4})’=\frac{1}{4}\times 2x d’après la 3ème formule du tableau n°2

(\frac{x^2}{4})’=\frac{x}{2}

(3x)’=3(x)’ d’après la 2ème formule du tableau n°1 

(3x)’=3\times 1 d’après la 2ème formule du tableau n°2

(3x)’=3

(1)’=0 d’après la 1ère formule du tableau n°2 

 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)=(\frac{x^3}{6}-\frac{x^2}{4}-3x+1)’\\f'(x)=(\frac{x^3}{6})’-(\frac{x^2}{4})’-(3x)’+(1)’\\f'(x)=\frac{1}{6}(x^3)’-\frac{1}{4}(x^2)’-3(x)’+(1)’\\f'(x)=\frac{1}{6}\times 3x^2-\frac{1}{4}\times 2x-3\times 1+0\\f'(x)=\frac{x^2}{2}-\frac{x}{2}-3

 

On veut étudier le signe de f'(x)=\frac{x^2}{2}-\frac{x}{2}-3.

On utilise la troisième ligne du tableau ci-dessous : la quantité est de la forme ax^2+bx+c.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On fait un tableau de signes comme en seconde.

On fait un tableau de signes comme en seconde.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

J’identifie les coefficients du polynôme. a=\frac{1}{2}, b=-\frac{1}{2} et c=-3.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par \frac{1}{2}, -\frac{1}{2} ,(-3)  .

\Delta=(-\frac{1}{2})²-4\times{\frac{1}{2}}\times{(-3)}\\\Delta=\frac{1}{4}+6

Pour ajouter; on met au même dénominateur , ici 4.

\Delta=\frac{1}{4}+6\times{\frac{4}{4}}\\\Delta=\frac{1}{4}+\frac{24}{4}\\\Delta=\frac{25}{4}

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par \frac{1}{2}, -\frac{1}{2}, \frac{25}{4}.

x_1=\frac{-(-\frac{1}{2})-\sqrt{\frac{25}{4}}}{2\times{\frac{1}{2}}}\\x_1=\frac{\frac{1}{2}-\frac{5}{2}}{1}\\x_1=-\frac{4}{2}\\x_1=-2

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par \frac{1}{2}, -\frac{1}{2}, \frac{25}{4}.

x_2=\frac{-(-\frac{1}{2})+\sqrt{\frac{25}{4}}}{2\times{\frac{1}{2}}}\\x_2=\frac{\frac{1}{2}+\frac{5}{2}}{1}\\x_2=\frac{6}{2}\\x_2=3

Je dresse le tableau de signes du polynôme:

Comme a=\frac{1}{2} le signe de a est positif.

 

 

 

On utilise la question précédente pour remplir la ligne du signe de f'(x).

On calcule f(-4) ,  f(-3) , f(2) et f(5) pour compléter la troisième ligne.

Pour cela, j’utilise la TI 83 Premium CE

 

 

On veut montrer que l’équation f(x)=0 admet trois solutions notées \alpha, \beta,\gamma sur l’intervalle [-4;5]

Pour bien visualiser la situation, on peut placer \alpha, \beta,\gamma sur la ligne des x et 0 sur la ligne des f(x) dans le tableau de variations comme ci-dessous.

  1. la fonction f est  continue et  strictement croissante sur l’intervalle [-4;-2].

Comme  0\in[-\frac{5}{3};\frac{14}{3}] alors l’équation f(x)=0 admet une unique solution notée \alpha sur l’intervalle [-4;-2].

2. la fonction f est  continue et  strictement décroissante sur l’intervalle [-2;3].

Comme  0\in[-\frac{23}{4};\frac{14}{3}] (il n’y a pas d’erreur, on écrit le plus petit nombre en premier) alors l’équation f(x)=0 admet une unique solution notée \beta sur l’intervalle [-2;3].

3. la fonction f est  continue et  strictement croissante sur l’intervalle [3;5].

Comme  0\in[-\frac{23}{4};\frac{7}{12}] alors l’équation f(x)=0 admet une unique solution notée \gamma sur l’intervalle [3;5].

 

 

Pour déterminer à la calculatrice TI 83 Premium CE une valeur approchée de  \alpha,\beta,\gamma.

On cherche les abscisses des points d’intersection de la courbe de f(x)=\frac{x^3}{6}-\frac{x^2}{4}-3x+1 et de y=0 (c’est-à-dire l’axe des abscisses) sur l’intervalle [-4;5] en procédant comme ci-dessous.

Une valeur approchée de \alpha à 10^{-2} près est -3.74.

Une valeur approchée de \beta à 10^{-2} près est 0.33.

Une valeur approchée de \alpha à 10^{-2} près est 4.91.

 

On veut déduire du tableau de variations le signe de f(x) sur l’intervalle [0;10].

Pour bien comprendre la situation, on peut placer son doigt à gauche du tableau de variations sur la ligne des f(x). Je place donc mon doigt sur -\frac{5}{3} qui est de signe – .

Je parcours les flèches de la gauche vers la droite en disant + ou  –.

Plutôt que de faire une phrase pour répondre à la question, on peut faire un tableau de signes.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.