Sommaire
- 1. Fonction logarithme népérien
- 1.1. Théorème et définition
- 1.2. Propriété
- 1.3. Courbe représentative
- 1.4. Propriété n°1
- 1.5. Exercice n°1
- 1.6. Exercice n°2
- 1.7. Propriété n°2
- 1.8. Exercice n°3
- 1.9. Propriété n°3
- 1.10. Exercice n°4
- 1.11. Propriété n°4
- 1.12. Exercice n°5
- 1.13. Propriété n°5
- 1.14. Exercice n°6
- 1.15. Propriété n°6
- 1.16. Exercice n°7
- 1.17. Propriété n°7
- 1.18. Exercice n°8
- 1.19. Propriété n°8
- 1.20. Exercice n°9
Fonction logarithme népérien
Théorème et définition
Pour tout réel a>0, l’équation e^x=a admet une solution unique dans \mathbf{R}. Cette solution se note x=ln(a) et se lit le logarithme népérien de a.
La fonction qui à x associe ln(x) s’appelle la fonction logarithme népérien. C’est la fonction réciproque de la fonction exponentielle. Elle est définie sur ]0;+\infty[.
Propriété
ln(1)=0 ln(e)=1
Courbe représentative
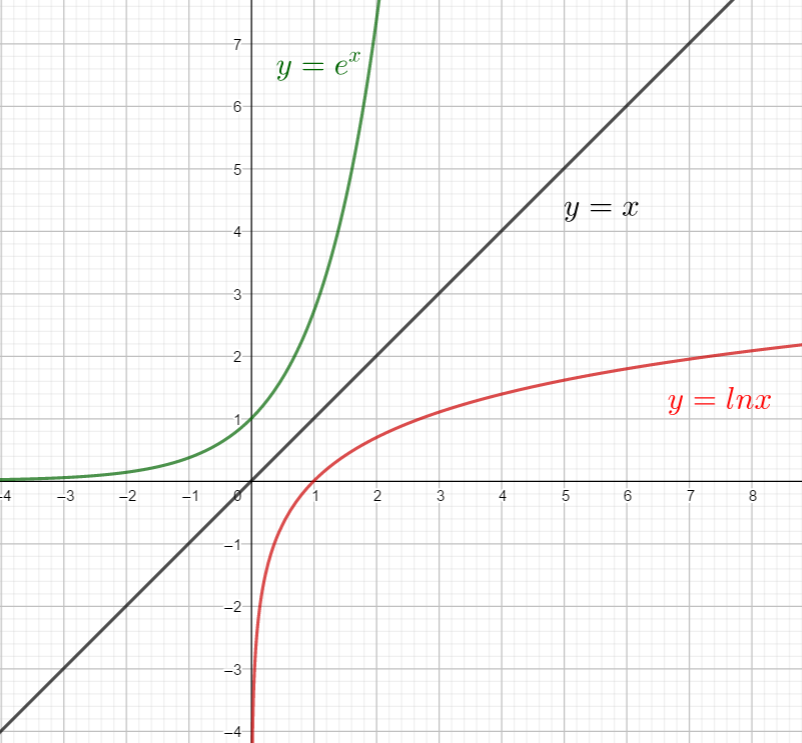
Dans la fenêtre Géogébra ci-dessous, tracer les courbes de f(x)=e^x et de g(x)=ln(x). Tracer aussi la droite d’équation y=x.
Comment sont ces deux courbes par rapport à la droite d’équation y=x ?
Propriété n°1
Pour tout réel y>0 et pour tout réel x , e^x=y \iff x=ln(y)
Exercice n°1
résoudre les équations suivantes
e^x=1
e^x=e
e^x=2
e^x=-2
Exercice n°2
résoudre les équations suivantes sur ]0;+\infty[
ln(x)=1
ln(x)=0
ln(x)=3
ln(x)=-2
Propriété n°2
Pour tout réel x>0 , e^{ln(x)}=x
Exercice n°3
résoudre les inéquations suivantes
e^x<1
e^{2x+2}\geq e
e^x>2
e^{-2x+1}\leq 3
Propriété n°3
Pour tout réel x , ln(e^x)=x
Exercice n°4
résoudre les inéquations suivantes
ln(x)>1 sur ]0;+\infty[
ln(x)\leq 0 sur ]0;+\infty[
ln(2x+4)<3
sur ]-2;+\infty[
ln(x)\geq -5 sur ]0;+\infty[
Propriété n°4
Pour tout réels a et b strictement positifs, ln(ab)=ln(a)+ln(b)
Exercice n°5
Exprimer les sommes suivantes en fonction de ln(2) et ln(5).
ln(4)+ln(25)-3ln(2)
ln(10)+ln(4)+3ln(2)
Propriété n°5
Pour tout entier naturel n, ln(a^n)=nln(a)
Exercice n°6
Exprimer les sommes suivantes en fonction de ln(3) et ln(5).
ln(15)+ln(3^4)-3ln(5^2)
ln(25)+ln(27)-2ln(5)
Propriété n°6
Pour tout réel a strictement positif, ln(\frac{1}{a})=-ln(a)
Exercice n°7
Exprimer les sommes suivantes en fonction de ln(2) et ln(7).
ln(\frac{1}{2})+ln(\frac{1}{7})+ln(14)
ln(\frac{1}{16})+ln(\frac{1}{49})-3ln(\frac{1}{2})
Propriété n°7
Pour tout réel a strictement positif, ln(\sqrt{a})=\frac{1}{2}ln(a)
Exercice n°8
Exprimer les sommes suivantes en fonction de ln(3) .
ln(\frac{1}{3})+ln(27)-ln(\sqrt{3})
ln(\frac{1}{9})+ln(81)-3ln(\sqrt{3})
Propriété n°8
Pour tout réels a et b strictement positifs , ln(\frac{a}{b})=ln(a)-ln(b)
Exercice n°9
Exprimer les sommes suivantes en fonction de ln(2) et ln(3) .
ln(\frac{2}{3})+ln(9)-ln(\sqrt{2})
ln(\frac{4}{3})+ln(8)-ln(6)