Sommaire
Variable aléatoire suivant une loi binomiale
Définition
On considère un schéma de Bernoulli constitué de n épreuves où la probabilité du succès est p .
X est la variable aléatoire qui donne le nombre de succès lors de ces épreuves.
La loi de probabilité de X est appelée loi binomiale de paramètres n et p et est notée B(n;p).
Exemple n°1
Un QCM comporte trois questions. Pour chacune d’elles quatre réponses sont proposées dont une seule est correcte.
Un élève répond au hasard à chaque question.
La variable X compte le nombre de réponses correctes données par l’élève.
C’est une épreuve de Bernoulli : on choisit une réponse parmi 4, la probabilité du succès est p=\frac{1}{4}.
C’est un schéma de Bernoulli : on répète 3 fois de façon indépendante une épreuve de Bernoulli donc n=3.
C’est une loi binomiale de paramètres n=3 et p=\frac{1}{4}. On la note B(3;\frac{1}{4}).
Exemple n°2
On jette une pièce de monnaie équilibrée trois fois de suite.
La variable X compte le nombre de faces obtenues.
C’est une épreuve de Bernoulli : il y a deux issues possibles : pile ou face, la probabilité du succès est p=\frac{1}{2}.
C’est un schéma de Bernoulli : on répète 3 fois de façon indépendante une épreuve de Bernoulli donc n=3.
C’est une loi binomiale de paramètres n=3 et p=\frac{1}{2}. On la note B(3;\frac{1}{2}).
Exemple n°3
On tire successivement 4 cartes dans un jeu de 32 cartes.
La variable X compte le nombre de rois obtenus.
C’est une épreuve de Bernoulli : il y a deux issues possibles : roi ou pas roi, la probabilité du succès est p=\frac{4}{32}=\frac{1}{8}.
C’est un schéma de Bernoulli : on répète 4 fois de façon indépendante une épreuve de Bernoulli donc n=4.
C’est une loi binomiale de paramètres n=4 et p=\frac{1}{8}. On la note B(4;\frac{1}{8}).
Probabilité de k succès
Propriété
X est une variable aléatoire qui suit une loi binomiale de paramètres n et p.
Alors, pour tout entier naturel k compris entre 0 et n, p(X=k)=\binom{n}{k}p^kq^{n-k} où q=1-p .
Remarque: p(X=k)se lit la probabilité d’obtenir k succès.
Exemple n°1
X suit une loi binomiale de paramètres n=4 et p=0.1
Calculer p(X=3).
Exemple n°2
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{2}
Calculer p(X=2)
Exemple n°3
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{4}
Calculer p(X=3).
Propriété
X est une variable aléatoire qui suit une loi binomiale de paramètres n et p.
Alors, E(X)=np, V(X)=npq et \sigma(X)=\sqrt{npq}.
Exemple n°1
X suit une loi binomiale de paramètres n=4 et p=0.1
Calculer E(X), V(X), \sigma(X).
Exemple n°2
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{2}
Calculer E(X), V(X), \sigma(X).
Exemple n°3
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{4}
Calculer E(X), V(X), \sigma(X).
Prolongement
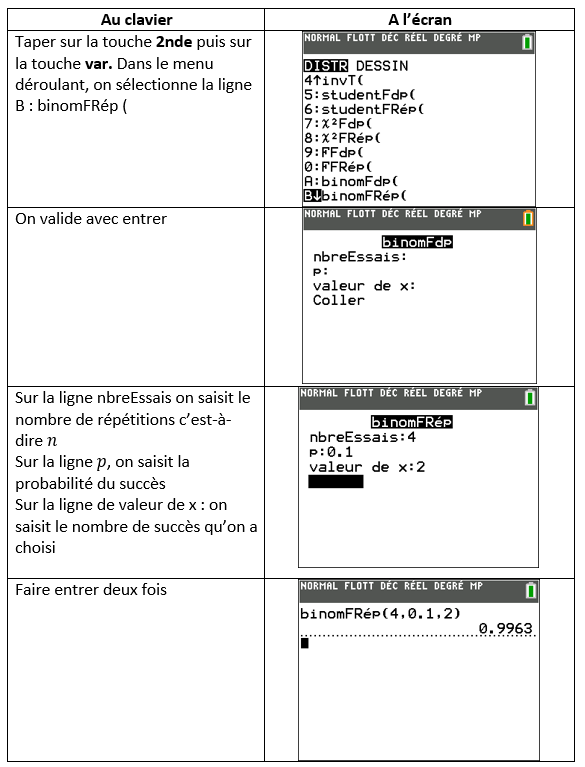
Comment calculer p(X\geq k) à l’aide de la calculatrice comme c’est indiqué dans les programmes ?
Exemple n°1
X suit une loi binomiale de paramètres n=4 et p=0.1
A l’aide de la calculatrice, calculer p(X\leq 2).
Exemple n°2
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{2}
A l’aide de la calculatrice, calculer p(X>1)
Exemple n°3
X suit une loi binomiale de paramètres n=3 et p=\frac{1}{4}
A l’aide de la calculatrice, calculer p(X\leq 2).
Exercice n°1
Alain et Benjamin pratiquent assidûment le tennis. Lorsqu’ils disputent un match l’un contre l’autre, est déclaré vainqueur le premier qui remporte deux manches.
Alain et Benjamin décident de faire un match.
On considère les évènements :
A_i : « Alain remporte la i-ième manche »;
B_i : « Benjamin remporte la i-ième manche ».
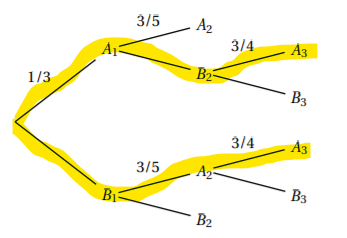
On donne ci-contre l’arbre pondéré présentant toutes les issues possibles de cette rencontre.
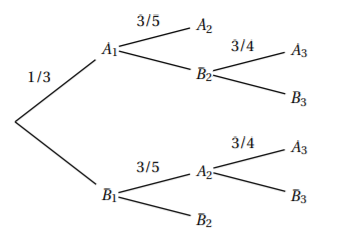
1. Quelle est la probabilité qu’Alain remporte ce match en trois manches ?
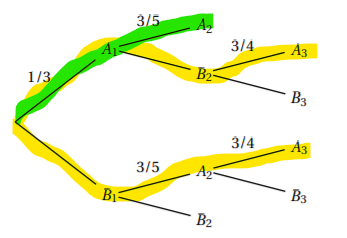
2. Démontrer que la probabilité qu’Alain gagne cette rencontre est 0.6.
3. Ils décident de jouer trois matchs dans l’année (les résultats des matchs sont indépendants les uns des autres) et de faire une cagnotte pour s’offrir un repas en fin d’année. À la fin de chaque match, le perdant versera 20 euros.
Benjamin s’interroge sur sa dépense éventuelle en fin d’année.
a. Quelles sont les dépenses possibles de Benjamin ?
b. Démontrer que la probabilité que Benjamin dépense 40 euros est 0.432.
c. Quelle est la loi de probabilité associée à la dépense possible de Benjamin ?
d. Calculer l’espérance de dépense en fin d’année pour Benjamin.
Exercice n°2
80 personnes s’apprêtent à passer le portique de sécurité. On suppose que pour chaque personne la probabilité que le portique sonne est égale à 0.02192.
Soit X la variable aléatoire donnant le nombre de personnes faisant sonner le portique, parmi les 80 personnes de ce groupe.
- Justifier que X suit une loi binomiale dont on précisera les paramètres.
2. Calculer l’espérance de X et interpréter le résultat.
3.a.Calculer la probabilité qu’au moins une personne du groupe fasse sonner le portique
3.b.Déterminer, à l’aide de la calculatrice, la probabilité qu’au maximum 5 personnes fassent sonner le portique.
Exercice n°3
Une agence de voyage propose des itinéraires touristiques pour lesquels chaque client effectue un
aller et un retour en utilisant soit un bateau, soit un train touristique. Le choix du mode de transport
peut changer entre l’aller et le retour.
À l’aller, le bateau est choisi dans 65 % des cas.
Lorsque le bateau est choisi à l’aller, il l’est également pour le retour 9 fois sur 10.
Lorsque le train a été choisi à l’aller, le bateau est préféré pour le retour dans 70 % des cas.
On interroge au hasard un client. On considère les évènements suivants :
• A : « le client choisit de faire l’aller en bateau »;
• R : « le client choisit de faire le retour en bateau ».
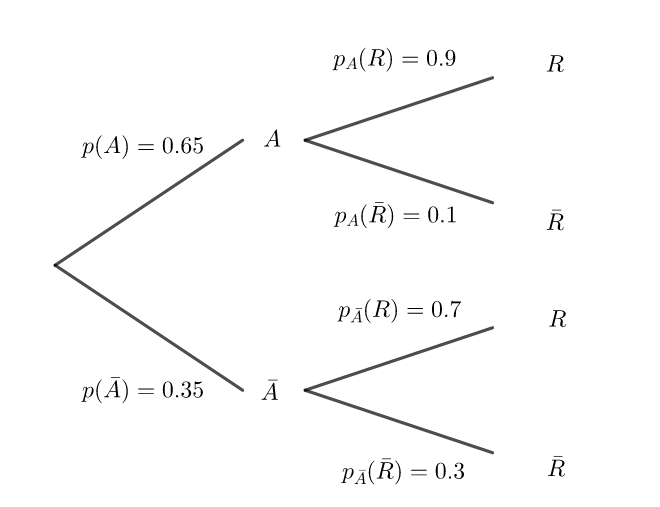
1. Traduire cette situation par un arbre pondéré.
2. On choisit au hasard un client de l’agence.
a. Calculer la probabilité que le client fasse l’aller-retour en bateau.
b. Montrer que la probabilité que le client utilise les deux moyens de transport est égale à
0,31.
3. On choisit au hasard 20 clients de cette agence. On note X la variable aléatoire qui compte le
nombre de clients qui utilisent les deux moyens de transport.
On admet que le nombre de clients est assez grand pour que l’on puisse considérer que X suit
une loi binomiale.
a. Préciser les paramètres de cette loi binomiale.
b. Déterminer la probabilité qu’exactement 12 clients utilisent les deux moyens de transport
différents.
c. Déterminer la probabilité qu’il y ait au moins 2 clients qui utilisent les deux moyens de transport différents.