Sommaire
Exercice n°1 : Session 15 Mars 2021 Sujet 1
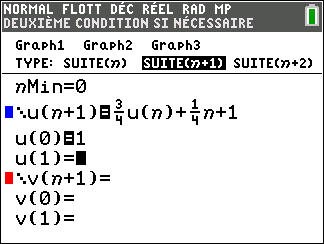
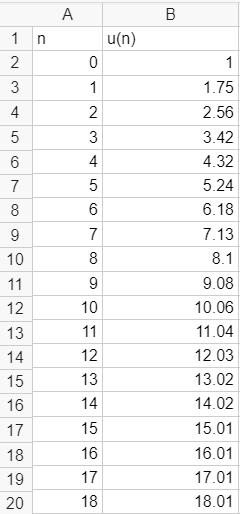
Soit (u_n) la suite définie sur \mathbf{N} par u_0=1 et u_{n+1}=\frac{3}{4}u_n+\frac{1}{4}n+1.
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
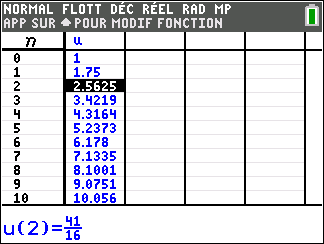
1. Calculer, en détaillant les calculs, u_1 et u_2.
2.a. Quelle valeur doit-on saisir dans la cellule B2 et quelle formule, étirée ensuite vers le bas, doit-on écrire dans la cellule B3 de la feuille de calcul Géogébra ci-dessous pour obtenir les termes successifs de la suite (u_n) dans la colonne B ?
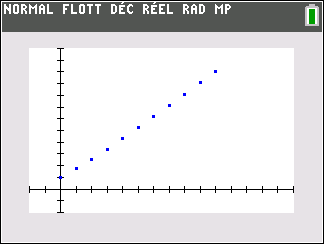
2.b. Conjecturer le sens de variation de la suite (u_n).
3. a. Démontrer par récurrence que, pour tout entier naturel n, on a : n\leq u_n\leq n+1.
3.b. En déduire, en justifiant la réponse, le sens de variation et la limite de la suite (u_n).
3.c. Démontrer que : lim_{n\to+\infty}\frac{u_n}{n}=1
4. On désigne par (v_n) la suite définie sur \mathbf{N} par v_n=u_n-n
a. Démontrer que la suite (v_n) est géométrique de raison \frac{3}{4}.
b. En déduire que, pour tout entier naturel n,on a : u_n=(\frac{3}{4})^n+n
Exercice n°2 : Session 15 Mars 2021 Sujet 2
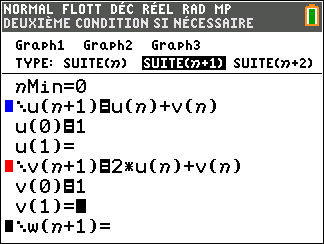
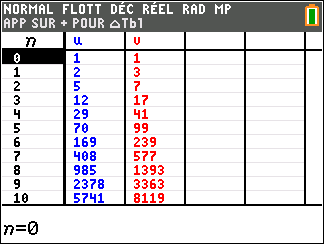
Soit (u_n) et (v_n) deux suites définies sur \mathbf{N} par
u_0=v_0=1
u_{n+1}=u_n+v_n
v_{n+1}=2u_n+v_n
Dans toute la suite de l’exercice, on admet que les suites (u_n) et (v_n) sont strictement positives.
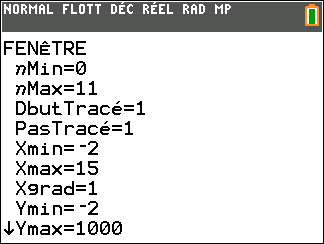
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
1.a. Calculer u_1 et v_1.
1.b. Démontrer que la suite (v_n) est strictement croissante, puis en déduire que, pour tout entier naturel n , v_n\geq 1.
1.c. Démontrer par récurrence que, pour tout entier naturel n , u_n\geq n+1.
1.d. En déduire la limite de la suite (u_n) .
2. On pose, pour tout entier naturel n
r_n=\frac{v_n}{u_n}
On admet que
r_n^2=2+\frac{(-1)^{n+1}}{u_n^2}
a. Démontrer que pour tout entier naturel n :
-\frac{1}{u_n^2}\leq \frac{(-1)^{n+1}}{u_n^2}\leq \frac{1}{u_n^2}
2.b. En déduire
lim_{n\to+\infty} \frac{(-1)^{n+1}}{u_n^2}
2.c. Déterminer la limite de la suite (r_n^2) et en déduire que (r_n) converge vers \sqrt{2}.
2.d. Démontrer que pour tout entier naturel n
r_{n+1}= \frac{2+r_n}{1+r_n}.
2.e. On considère le programme suivant écrit en langage Python :

(abs désigne la valeur absolue, sqrt la racine carrée et 10** (-4) représente 10^{-4}).
Quelle valeur de n est renvoyée par ce programme ?
À quoi correspond-elle ?
Exercice n°3 : Amérique du Nord Mai 2021
Un biologiste s’intéresse à l’évolution de la population d’une espèce animale sur une île du Pacifique.
Au début de l’année 2020, cette population comptait 600 individus. On considère que l’espèce sera menacée d’extinction sur cette île si sa population devient inférieure ou égale à 20 individus.
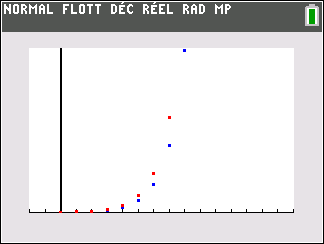
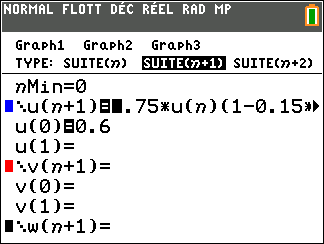
Le biologiste modélise le nombre d’individus par la suite (u_n) définie par :
u_0=0.6
u_{n+1}=0.75u_n(1-0.15u_n)
où pour tout entier naturel n, u_n désigne le nombre d’individus, en milliers, au début de l’année 2020+n.
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
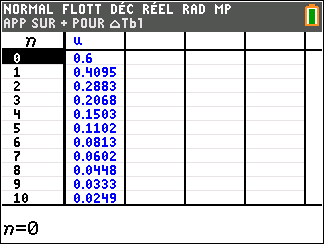
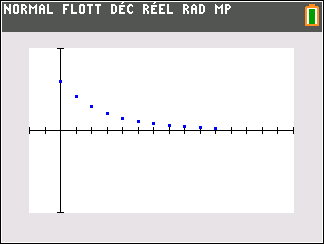
1. Estimer, selon ce modèle, le nombre d’individus présents sur l’île au début de l’année 2021 puis au début de l’année 2022.
Soit f la fonction définie sur l’intervalle [0;1] par f(x)=0.75x(1-0.15x) .
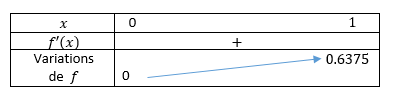
2. Montrer que la fonction f est croissante sur l’intervalle [0;1] et dresser son tableau de variations.
3. Résoudre dans l’intervalle [0;1] l’équation f(x)=x.
On remarquera pour la suite de l’exercice que, pour tout entier naturel n , u_{n+1}=f(u_n).
4. a. Démontrer par récurrence que pour tout entier naturel n,
0\leq u_{n+1}\leq u_n\leq 1.
4.b. En déduire que la suite (u_n) est convergente.
4.c. Déterminer la limite l de la suite (u_n).
5. Le biologiste a l’intuition que l’espèce sera tôt ou tard menacée d’extinction.
a. Justifier que, selon ce modèle, le biologiste a raison.
b. Le biologiste a programmé en langage Python la fonction menace() ci-dessous :

Donner la valeur numérique renvoyée lorsqu’on appelle la fonction menace().
Interpréter ce résultat dans le contexte de l’exercice. :
Exercice n°4 : Polynésie 2 Juin 2021
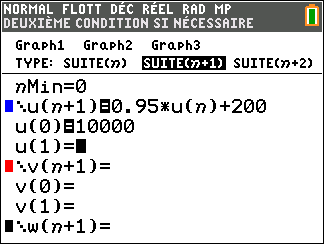
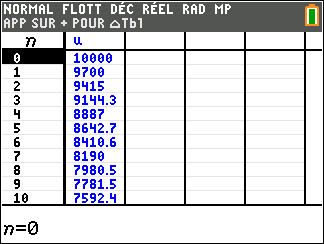
Soit (u_n) la suite définie sur \mathbf{N} par u_0=10000 et u_{n+1}=0.95u_n+200.
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
1. Calculer u_1 et vérifier que u_2=9415.
2. a. Démontrer, à l’aide d’un raisonnement par récurrence, que pour tout entier naturel n :
u_n>4000.
b. On admet que la suite (u_n) est décroissante. Justifier qu’elle converge.
3. Pour tout entier naturel n, on considère la suite (v_n) définie par : v_n=u_n-4000.
a. Calculer v_0.
b. Démontrer que la suite (v_n) est géométrique de raison égale à 0.95.
c. En déduire que pour tout entier naturel n:
u_n=4000+6000\times 0.95^n.
d. Quelle est la limite de la suite (u_n)? Justifier la réponse.
4. En 2020, une espèce animale comptait 10000 individus. L’évolution observée les années précédentes conduit à estimer qu’à partir de l’année 2021, cette population baissera de 5 % chaque début d’année.
Pour ralentir cette baisse, il a été décidé de réintroduire 200 individus à la fin de chaque année, à partir de 2021.
Une responsable d’une association soutenant cette stratégie affirme que : « l’espèce ne devrait pas s’éteindre, mais malheureusement, nous n’empêcherons pas une disparition de plus de la moitié de la population ».
Que pensez-vous de cette affirmation ? Justifier la réponse.
Exercice n°5 : Asie 7 Juin 2021
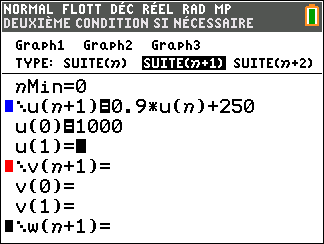
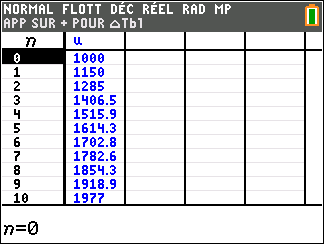
En 2020, une influenceuse sur les réseaux sociaux compte 1000 abonnés à son profil. On modélise le nombre d’abonnés ainsi : chaque année, elle perd 10 % de ses abonnés auxquels s’ajoutent 250 nouveaux abonnés.
Pour tout entier naturel n, on note un le nombre d’abonnés à son profil en l’année (2020+n), suivant cette modélisation, u_0=1000.
1. Calculer u_1.
2. Justifier que pour tout entier naturel n ,
u_{n+1}=0.9u_n+250.
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
3. La fonction Python nommée « suite » est définie ci-dessous. Dans le contexte de l’exercice, interpréter la valeur renvoyée par suite(10).

4. a. Montrer, à l’aide d’un raisonnement par récurrence, que pour tout entier naturel n ,
u_{n}\leq 2500.
4.b. Démontrer que la suite (u_n) est croissante.
4.c. Déduire des questions précédentes que la suite (u_n) est convergente.
5. Soit (v_n) la suite définie par v_n=u_n-2500 pour tout entier naturel n.
a. Montrer que la suite (v_n) est une suite géométrique de raison 0.9 et de terme initial v_0=-1500.
b. Pour tout entier naturel n, exprimer v_n en fonction de n et montrer que :
u_n=-1500\times 0.9^n+2500.
c. Déterminer la limite de la suite (u_n) et interpréter dans le contexte de l’exercice
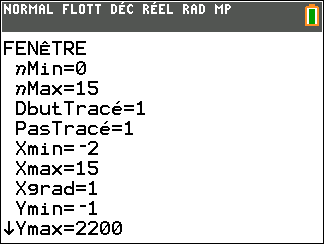
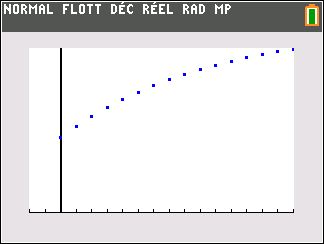
6. Écrire un programme qui permet de déterminer en quelle année le nombre d’abonnés dépassera 2200.
Déterminer cette année
Exercice n°6 : Centres Etrangers 9 Juin 2021
En mai 2020, une entreprise fait le choix de développer le télétravail afin de s’inscrire dans une démarche écoresponsable.
Elle propose alors à ses 5000 collaborateurs en France de choisir entre le télétravail et le travail au sein des locaux de l’entreprise.
En mai 2020, seuls 200 d’entre eux ont choisi le télétravail.
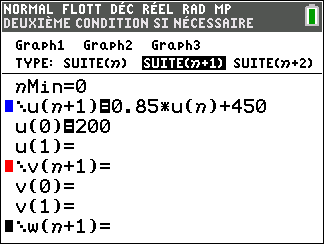
Chaque mois, depuis la mise en place de cette mesure, les dirigeants de l’entreprise constatent que 85 % de ceux qui avaient choisi le télétravail le mois précédent choisissent de continuer, et que, chaque mois, 450 collaborateurs supplémentaires choisissent le télétravail.
On modélise le nombre de collaborateurs de cette entreprise en télétravail par la suite (a_n).
Le terme a_n désigne ainsi une estimation du nombre de collaborateurs en télétravail le n-ième mois après le mois de mai 2020. Ainsi a_0=200.
Partie A :
1. Calculer a_1.
2. Justifier que pour tout entier naturel n , a_{n+1}=0.85a_n+450.
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
3. On considère la suite (v_n) définie pour tout entier naturel n par : v_{n}=a_n-3000.
a. Démontrer que la suite (v_n) est une suite géométrique de raison 0.85 et de premier terme -2800.
b. Exprimer v_n en fonction de n.
c. En déduire que, pour tout entier naturel n , a_n=-2800\times 0.85^n+3000.
4. Déterminer le nombre de mois au bout duquel le nombre de télétravailleurs sera strictement supérieur à 2500, après la mise en place de cette mesure dans l’entreprise.
Partie B :
Afin d’évaluer l’impact de cette mesure sur son personnel, les dirigeants de l’entreprise sont parvenus à modéliser le nombre de collaborateurs satisfaits par ce dispositif à l’aide de la suite (u_n) définie par u_0=1 et, pour tout entier naturel n , u_{n+1}=\frac{5u_n+4}{u_n+2}
où u_n désigne le nombre de milliers de collaborateurs satisfaits par cette nouvelle mesure au bout de n mois après le mois de mai 2020.
1. Démontrer que la fonction f définie pour tout x\in[0;+\infty[ par f(x)=\frac{5x+4}{x+2} est strictement croissante sur [0;+\infty[.
2. a. Démontrer par récurrence que pour tout entier naturel n,
0\leq u_{n}\leq u_{n+1}\leq 4
b. Justifier que la suite (u_n) est convergente.
3. On admet que pour tout entier naturel n, 0\leq 4-u_n\leq 3\times (\frac{1}{2})^n.
En déduire la limite de la suite (u_n) et l’interpréter dans le contexte de la modélisation.
Exercice n°7 : Métropole 13 Septembre 2021 J1
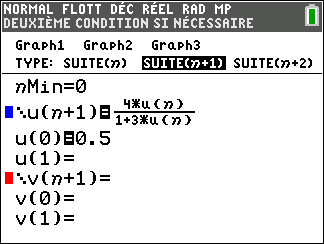
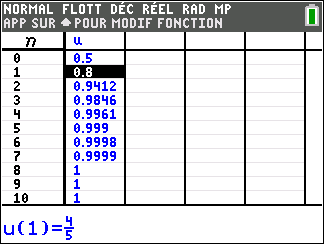
Soit la fonction f définie pour tout x\in]-\frac{1}{3};+\infty[ par f(x)=\frac{4x}{1+3x}.
On considère la suite (u_n) définie par : u_0=\frac{1}{2}
et, pour tout entier naturel n, u_{n+1}=f(u_n).
Avant de commencer, il est bon de programmer sa TI 83 Premium CE.
1. Calculer u_1.
2. On admet que la fonction f est croissante sur l’intervalle ]-\frac{1}{3};+\infty[¸
a. Montrer par récurrence que, pour tout entier naturel n, on a :
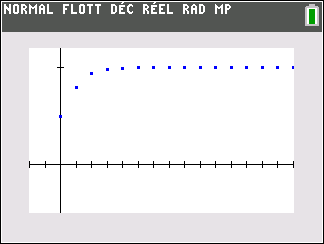
\frac{1}{2}\leq u_{n}\leq u_{n+1}\leq 2
b. En déduire que la suite (u_n) est convergente.
c. On appelle l la limite de la suite (u_n) . Déterminer la valeur de l.
3. a. Recopier et compléter la fonction Python ci-dessous qui, pour tout réel positif E,
détermine la plus petite valeur p tel que : 1-u_p<E.

b. Donner la valeur renvoyée par ce programme dans le cas où E=10^{-4}.
4. On considère la suite (v_n) définie, pour tout entier naturel n , par :
v_n=\frac{u_n}{1-u_n}
a. Montrer que la suite (v_n) est géométrique de raison 4.
En déduire, pour tout entier naturel n, l’expression de v_n en fonction de n.
b. Démontrer que, pour tout entier naturel n , on a :
u_n=\frac{v_n}{v_n+1}
c. Montrer alors que, pour tout entier naturel n , on a :
u_n=\frac{1}{1+0.25^n}Retrouver par le calcul la limite de la suite (u_n).