logo

2. Factoriser en seconde

Sommaire

Factoriser à l’aide d’un facteur commun.

a) Activité d’approche: ABEF est un rectangle de dimensions a et b.

                                     BCDE est un rectangle de dimensions a et c.

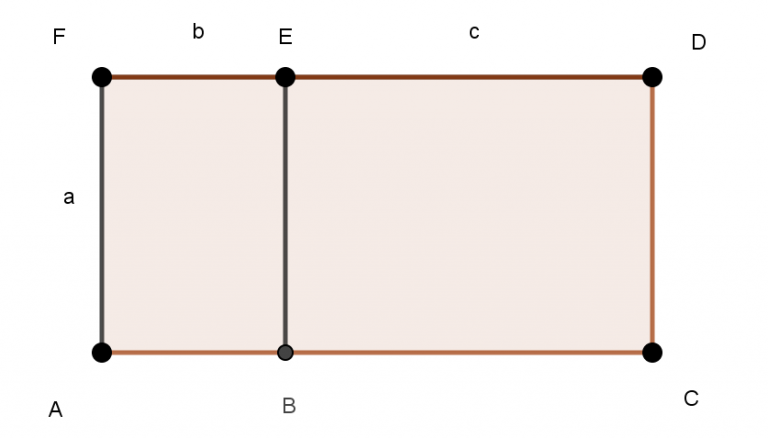
1) a) Exprimer l’aire de ABEF en utilisant les lettres a, b, c .

correction

b) Exprimer l’aire de BCDE en utilisant les lettres a, b, c .

correction

c) Déduire des questions précédentes l’aire totale de ACDF.

correction

2) a) Exprimer la distance FD en utilisant les lettres a, b, c .

correction

b) En déduire une nouvelle écriture de l’aire de ACDF en utilisant les lettres a, b, c .

correction

3) Compléter les pointillés en utilisant les résultats des questions 1) et 2) :

ab+…=a(…+…)
correction

b) Méthode: Si vous avez trouvé un facteur commun aux deux termes d’une somme, écrire les deux termes sous la forme de deux produits de deux facteurs dont l’un est commun aux deux. Utiliser le diagramme suivant.

Premier terme        =   facteur commun   \times  deuxième facteur n°1

Deuxième terme    =   facteur commun     \timesdeuxième facteur n°2

                  puis écrire la somme sous la forme

facteur commun    ( deuxième facteur n°1  + ( ou –) deuxième facteur n°2)

Remarque : il faut mettre en facteur le plus grand facteur possible.

Exercice n°1: Factoriser à l’aide du facteur commun dans chaque cas.

 1) 2x-6y

méthode
correction

2)  3x^{2}-6x 

méthode
correction

3)  5x^{2}-x 

méthode
correction

4)  2x^{2}-4x+6 

méthode
correction

5)  30x^{2}-18x+27 

méthode
correction

Après avoir répondu aux questions, utiliser la fenêtre Géogébra ci-dessous pour valider les réponses. Pour cela saisir par exemple 2x-6y puis cliquer sur le quatrième onglet en haut à partir de la gauche. Sur le ligne en dessous apparaît Factoriser 2(x-3y).

Factoriser à l’aide d’une identité remarquable

 Activité d’approche: Voici la figure ci-dessous où ACEG, BCDH, et IHFG sont des carrés.    

On note a, la longueur GF et b, la longueur FE.

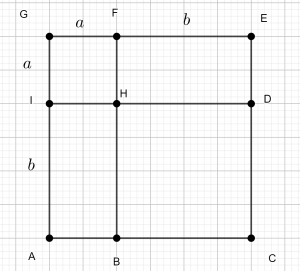
1)     Exprimer les aires des carrés IHFG et HDCB en fonction de a et b.

correction

2) Exprimer les aires des rectangles FEDH et IHBA en fonction de a et b.

correction

3) Déduire des questions 1) et 2) l’aire du carré ACEG par découpage, en fonction de a et b.

correction

4) Combien mesure la longueur GE en fonction de a et b ? Exprimer alors l’aire du carré ACEG en fonction de a et b, en utilisant la formule de l’aire d’un carré.

correction

5) En utilisant les résultats des questions 3) et 4). Compléter les pointillés :

a^{2}+…+…=(…+…)^{2}
correction

Factoriser à l’aide de la première identité remarquable

a^{2}+2ab+b^{2}=(a+b)^{2}

Méthode

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

Exercice n°2: Factoriser les expressions suivantes

  1.   x^{2}+6x+9 
méthode
correction

2.   x^{2}+8x+16 

méthode
correction

 3.   4x^{2}+4x+1 

méthode
correction

4.   9x^{2}+24x+16 

méthode
correction

5.   \frac{x^{2}}{4}+\frac{2x}{3}+\frac{4}{9} 

méthode
correction

6. x^{2}+2\sqrt{3}x+3 

méthode
correction

Après avoir répondu aux questions, utiliser la fenêtre Géogébra ci-dessous pour valider les réponses. Pour cela saisir par exemple x^{2}+6x+9  puis cliquer sur le quatrième onglet en haut à partir de la gauche. Sur le ligne en dessous apparaît Factoriser (x+3)^2.

Pour saisir racine carrée de 3, taper sqrt(3).

Factoriser à l’aide de la seconde identité remarquable

a^{2}-2ab+b^{2}=(a-b)^{2}

Méthode

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

Exercice n°3: Factoriser les expressions suivantes

  1.   9x^{2}-12x+4 
méthode
correction

2.   \frac{x^{2}}{25}-\frac{x}{5}+\frac{1}{4} 

méthode
correction

3.   x^{2}-22x+121 

méthode
correction

4.   \frac{x^{2}}{16}-\frac{x}{2}+1 

méthode
correction

Après avoir répondu aux questions, utiliser la fenêtre Géogébra ci-dessous pour valider les réponses. Pour cela saisir par exemple 9x^{2}-12x+4   puis cliquer sur le quatrième onglet en haut à partir de la gauche. Sur le ligne en dessous apparaît Factoriser (3x-2)^2.

Factoriser à l’aide de la troisième identité remarquable 

a^{2}–b^{2}=(a-b)(a+b)

Méthode

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

Exercice n°4: Factoriser les expressions suivantes

  1.   x^{2}-100 
méthode
correction

2.   25x^{2}-121 

méthode
correction

3.   49x^{2}-\frac{25}{36} 

méthode
correction

4.  x^{2}-2 

méthode
correction

5.  (x-1)^{2}-4 

méthode
correction

6.  (2x-3)^{2}-81 

méthode
correction

7.  (2x-2)^{2}-(x+1)^{2} 

méthode
correction

Après avoir répondu aux questions, utiliser la fenêtre Géogébra ci-dessous pour valider les réponses. Pour cela saisir par exemple x^2-100   puis cliquer sur le quatrième onglet en haut à partir de la gauche. Sur le ligne en dessous apparaît Factoriser (x-10)(x+10).

 Factoriser à l’aide d’un facteur commun et d’une identité remarquable 

Exercice n°5 : Factoriser les expressions suivantes

  1.   3(2x-7)^2-3 
correction

2.   6(x+4)^2-18 

correction

3.   7(3+2x)^2-28 

correction

©2020 – Math’O karé SAS

L’aire du rectangle ABEF est égale au produit AF\times FE=a\times b

 

L’aire du rectangle BCDE est égale au produit BE\times ED=a\times c

 

L’aire totale du rectangle ACDF est égale à la somme des aires des rectangles  ABEF  et BCDE ,

c’est-à-dire a\times b+a\times c

La distance FD=FE+ED=b+c

L’aire totale du rectangle ACDF est égale à AF\times FD=a\times(b+c)

ab+ac=a\times(b+c)

 Méthode: Si vous avez trouvé un facteur commun aux deux termes d’une somme, écrire les deux termes sous la forme de deux produits de deux facteurs dont l’un est commun aux deux. Utiliser le diagramme suivant.

Premier terme        =   facteur commun   \times  deuxième facteur n°1

Deuxième terme    =   facteur commun     \times deuxième facteur n°2

Puis écrire la somme sous la forme

facteur commun    ( deuxième facteur n°1  + ( ou –) deuxième facteur n°2)

Factorisons 2x-6y\\2x={2}\times{x}\\6y={2}\times{3y}\\2x-6y=2(x-3y)

Factorisons 3x^{2}-6x\\3x^{2}={3x}\times{x}\\6x={3x}\times{2}\\3x^{2}-6x=3x(x-2)

Factorisons 5x^{2}-x\\5x^{2}={x}\times{5x}\\x={x}\times{1}\\5x^{2}-x=x(5x-1)

 Méthode: Si vous avez trouvé un facteur commun aux trois termes d’une somme, écrire les trois  termes sous la forme de trois produits de deux facteurs dont l’un est commun aux trois. Utiliser le diagramme suivant.

Premier terme        =   facteur commun   \times  deuxième facteur n°1

Deuxième terme    =   facteur commun     \timesdeuxième facteur n°2

Troisième terme    =   facteur commun     \timesdeuxième facteur n°3

 Puis écrire la somme sous la forme

facteur commun    ( deuxième facteur n°1  + ( ou –) deuxième facteur n°2+ ( ou –) deuxième facteur n°3)

Factorisons 2x^{2}-4x+6\\2x^{2}={2}\times{x^{2}}\\4x={2}\times{2x}\\6={2}\times{3}\\2x^{2}-4x+6=2(x^{2}-2x+3)

Factorisons 30x^{2}-18x+27\\30x^{2}={3}\times{10x^{2}}

18x={3}\times{6x}27={3}\times{9}

 

30x^{2}-18x+27=3(10x^{2}-6x+9)

L’aire du carré IHGF est égale à GF^{2}=a^{2}

L’aire du carré HDCB est égale à HD^{2}=b^{2}

L’aire du rectangle FEDH est égale au produit FH\times FE=a\times b

L’aire du rectangle IHBA est égale au produit IH\times IA=a\times b

L’aire totale du carré ACEG est égale à la somme des aires des carrés et des rectangles c’est-à-dire

a^{2}+ab+ab+b^{2} ou a^{2}+2ab+b^{2}

La distance GE=a+b

L’aire totale du carré ACEG est égale à GE^{2}=(a+b)^{2}

a^{2}+2ab+b^{2}=(a+b)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=x^{2} donc a=x

b^{2}=9  donc b=3

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{3}=6x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+6x +9= (x+3)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=x^{2} donc a=x

b^{2}=16  donc b=4

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{4}=8x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+8x +16= (x+4)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=4x^{2} donc a=2x

b^{2}=1  donc b=1

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{2x}\times{1}=4x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

4x^{2}+4x +1= (2x+1)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=9x^{2} donc a=3x

b^{2}=16  donc b=4

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{3x}\times{4}=24x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

9x^{2}+24x +16= (3x+4)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=\frac{x^{2}}{4} donc a=\frac{x}{2}

b^{2}=\frac{4}{9} donc b=\frac{2}{3}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{2}}\times{\frac{2}{3}}=\frac{2x}{3}

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

\frac{x^{2}}{4}+\frac{2x}{3} +\frac{4}{9}= (\frac{x}{2}+\frac{2}{3})^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=x^{2} donc a=x\\b^{2}=3  donc b=\sqrt{3}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{\sqrt{3}}=2\sqrt{3}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+2\sqrt{3}x +3= (x+\sqrt{3})^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=9x^{2} donc a=3x

b^{2}=4 donc b=2

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{3x}\times{2}=12x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

9x^{2}-12x +4= (3x-2)^{2}

a^{2}=\frac{x^{2}}{25} donc a=\frac{x}{5}

b^{2}=\frac{1}{4} donc b=\frac{1}{2}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{5} }\times{\frac{1}{2} }=\frac{x}{5}

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

\frac{x^{2}}{25}-\frac{x}{5}+\frac{1}{4}= (\frac{x}{5} -\frac{1}{2})^{2}

a^{2}=x^{2} donc a=x\\b^{2}=121  donc b=11

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{11}=22x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

x^{2}-22x +121= (x-11)^{2}

a^{2}=\frac{x^{2}}{16} donc a=\frac{x}{4} \\b^{2}=1  donc b=1

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{4}}\times{1}=\frac{x}{2}

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

\frac{x^{2}}{16} -\frac{x}{2} +1= (\frac{x}{4}-1)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

a^{2}=x^{2}  donc a=x

b^{2}=100  donc b=10

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

x^{2}-100= (x-10)(x+10)

a^{2}=25x^{2}  donc a=5x

b^{2}=121  donc b=11

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

25x^{2}-121= (5x-11)(5x+11)

a^{2}=49x^{2}  donc a=7x

b^{2}=\frac{25}{36}  donc b=\frac{5}{6}

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

49x^{2}-\frac{25}{36}  = (7x-\frac{5}{6})(7x+\frac{5}{6})

a^{2}=x^{2}  donc a=x

b^{2}=2  donc b=\sqrt{2}

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

x^{2}-2= (x-\sqrt{2})(x+\sqrt{2})

a^{2}=(x-1)^{2}  donc a=x-1

b^{2}=4 donc b=2

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

(x-1)^{2}-4= (x-1-2)(x-1+2)\\(x-1)^{2}-4= (x-3)(x+1)

a^{2}=(2x-3)^{2}  donc a=2x-3

b^{2}=81 donc b=9

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

(2x-3)^{2}-81= (2x-3-9)(2x-3+9)\\(2x-3)^{2}-81= (2x-12)(2x+6)

a^{2}=(2x-2)^{2}  donc a=2x-2

b^{2}=(x+1)^{2} donc b=x+1

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

(2x-2)^{2}-(x+1)^{2} = ((2x-2)-(x+1))(2x-2)+(x+1))\\\hspace{3.2cm} = (2x-2-x-1))(2x-2+x+1))\\\hspace{3.2cm} = (x-3)(3x-1)

On veut factoriser 3(2x-7)^2-3=

1. Il y a un facteur commun, ici 3.

 Utiliser le diagramme suivant.

3(2x-7)^2=  =   3 \times (2x-7)^2

3   =   3 \times 1

puis écrire la somme sous la forme

3(2x-7)^2-3=3  ((2x-7)^2– 1)

2. on utilise l’identité remarquable a^{2}-b^{2}= (a-b)(a+b) pour factoriser ((2x-7)^2-1

a^{2}=(2x-7)^2 donc a=2x-7

b^{2}=1 donc b=1

Pour finir, il suffit de remplacer a, b , a^{2} et b^{2} par leurs valeurs dans a^{2}-b^{2}= (a-b)(a+b).

(2x-7)^2-1= (2x-7-1)(2x-7+1)\\\hspace{2.1cm}= (2x-8)(2x-6)

3. On termine :

3(2x-7)^2-3=3(2x-8)(2x-6)

 

On veut factoriser 6(x+4)^2-18=

1. Il y a un facteur commun, ici 6.

 Utiliser le diagramme suivant.

6(x+4)^2=  =   6 \times (x+4)^2

18   =   6 \times 3

puis écrire la somme sous la forme

6(x+4)^2-18=6  ((x+4)^2– 3)

2. on utilise l’identité remarquable a^{2}-b^{2}= (a-b)(a+b) pour factoriser ((x+4)^2-3

a^{2}=(x+4)^2 donc a=x+4

b^{2}=3 donc b=\sqrt{3}

Pour finir, il suffit de remplacer a, b , a^{2} et b^{2} par leurs valeurs dans a^{2}-b^{2}= (a-b)(a+b).

(x+4)^2-3= (x+4-\sqrt{3})(x+4+\sqrt{3})

3. On termine :

6(x+4)^2-18=6(x+4-\sqrt{3})(x+4+\sqrt{3})

On veut factoriser 7(3+2x)^2-28=

1. Il y a un facteur commun, ici 7.

 Utiliser le diagramme suivant.

7(3+2x)^2=  =   7 \times (3+2x)^2

28   =   7 \times 4

puis écrire la somme sous la forme

7(3+2x)^2-28=7  ((3+2x)^2– 4)

2. on utilise l’identité remarquable a^{2}-b^{2}= (a-b)(a+b) pour factoriser ((3+2x)^2-4

a^{2}=(3+2x)^2 donc a=3+2x

b^{2}=4 donc b=2

Pour finir, il suffit de remplacer a, b , a^{2} et b^{2} par leurs valeurs dans a^{2}-b^{2}= (a-b)(a+b).

(3+2x)^2-4= (3+2x-2)(3+2x+2)\\\hspace{2.1cm}= (2x+1)(2x+5)

3. On termine :

7(3+2x)^2-28=7(2x+1)(2x+5)

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.