logo

T. Calcul intégral

Intégrale d’une fonction continue et positive

Sommaire

Définition

On appelle unité d’aire (u.a.) l’aire du rectangle de côtés [OI] et [OJ].

Soit f une fonction continue et positive sur un intervalle [a;b].

On appelle intégrale de a à b de f , l’aire exprimée en u.a.  délimitée par la courbe C_f , l’axe des abscisses et les droites verticales d’équations x=a et x=b.

Cette intégrale se note \int_a^b f(x)\hspace{0.05cm}dx

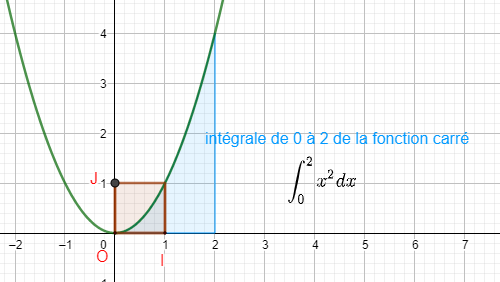
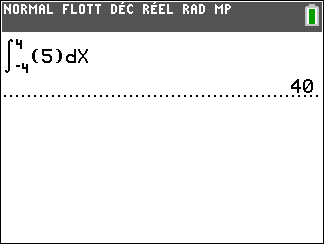
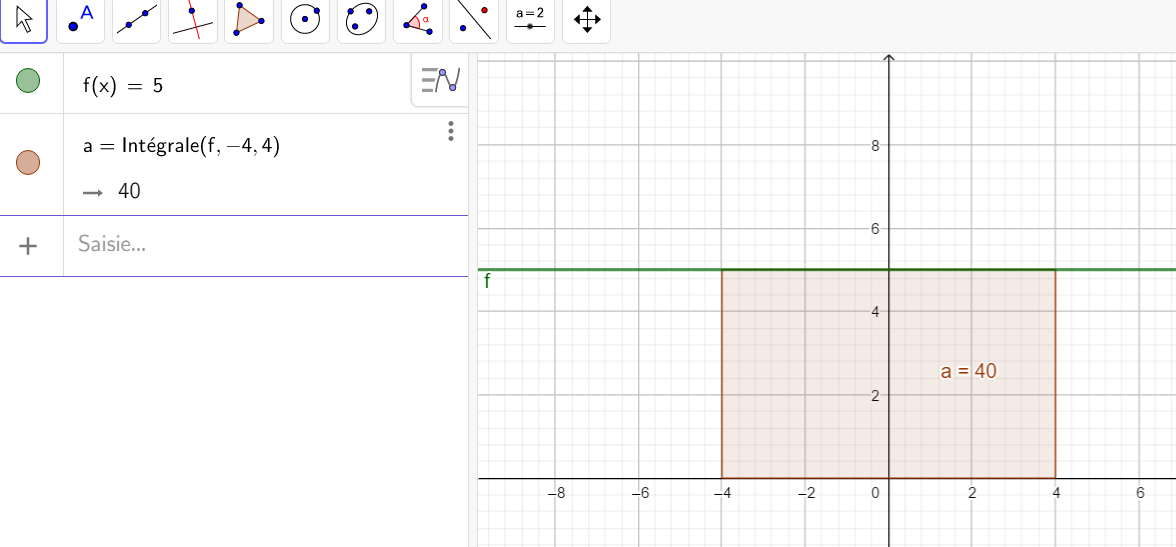
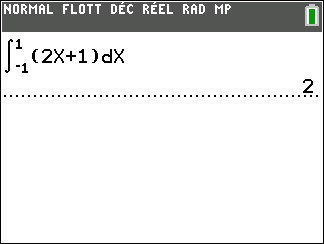
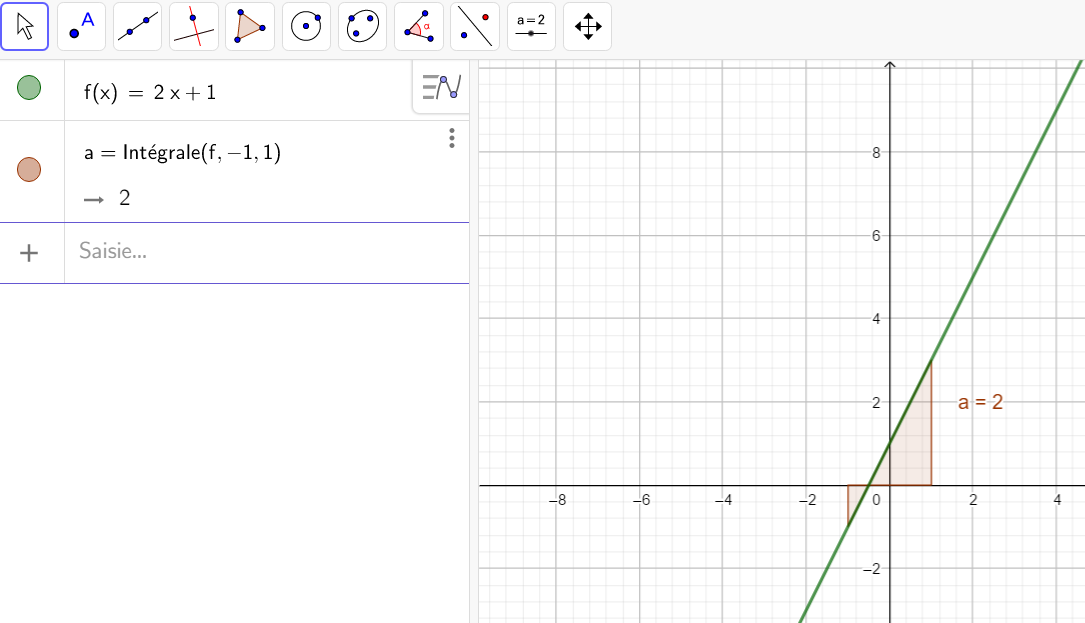
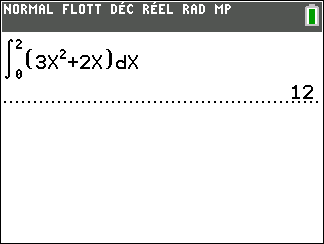
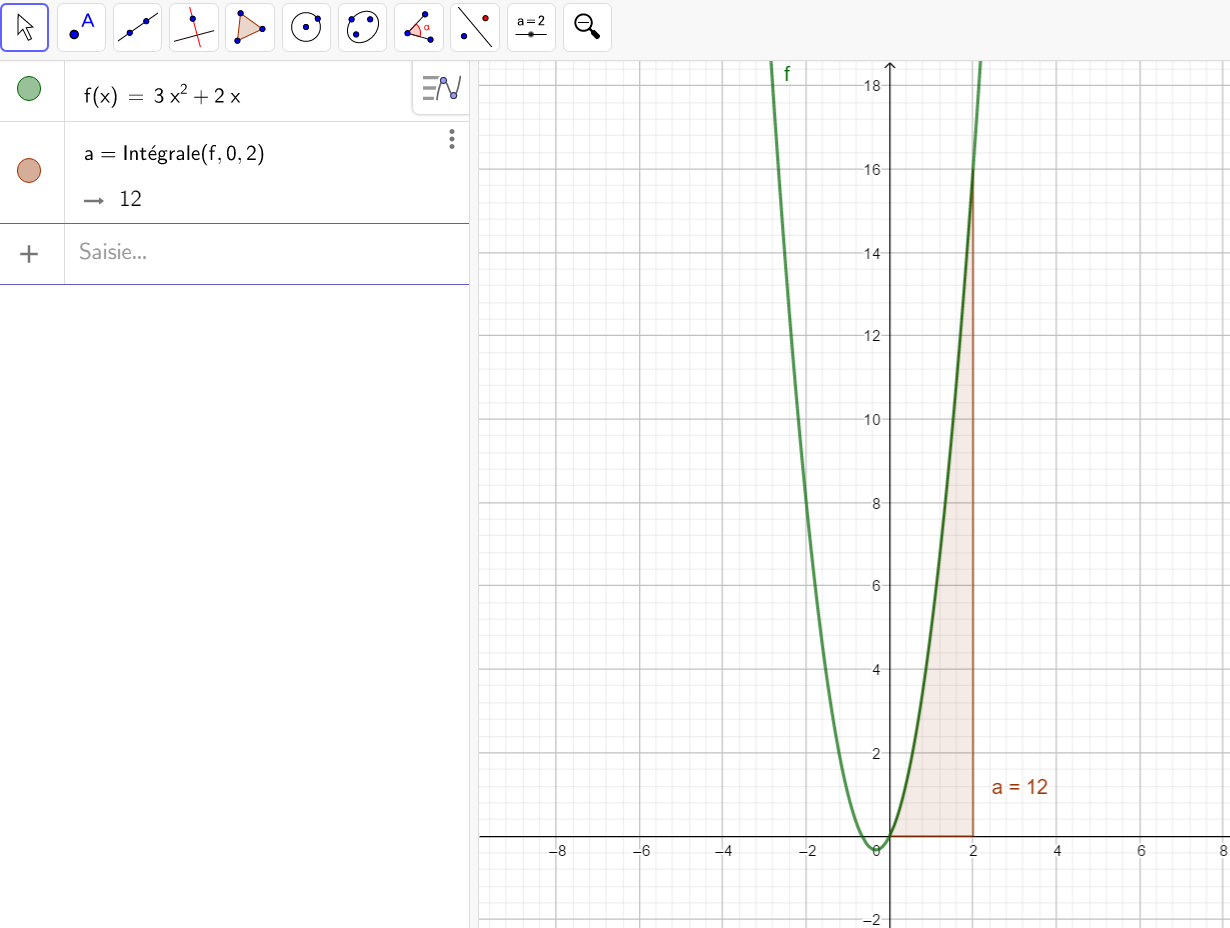
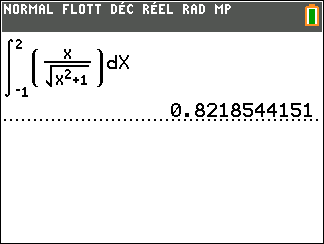
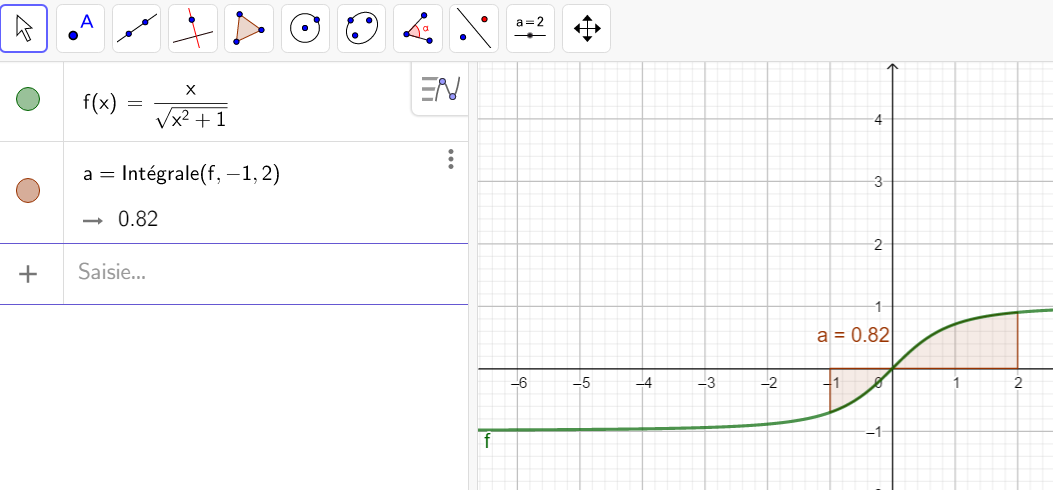
Calculer une intégrale avec Géogébra

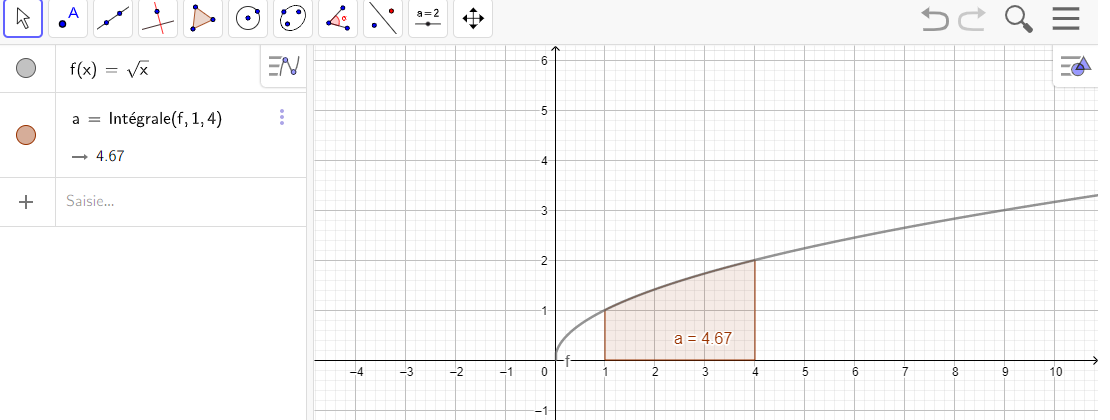
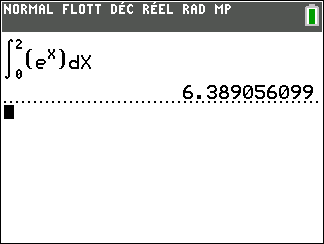
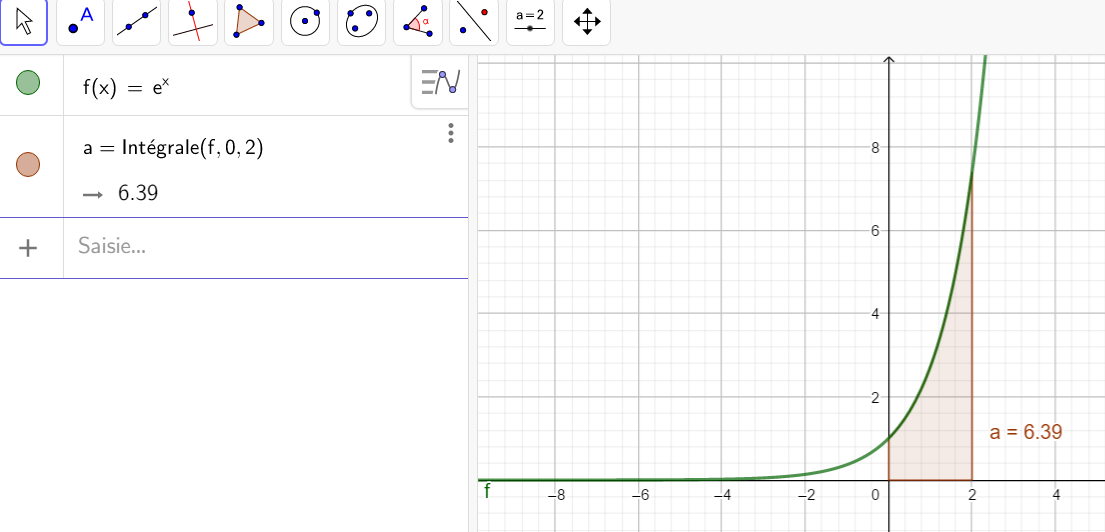
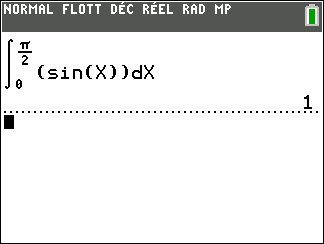
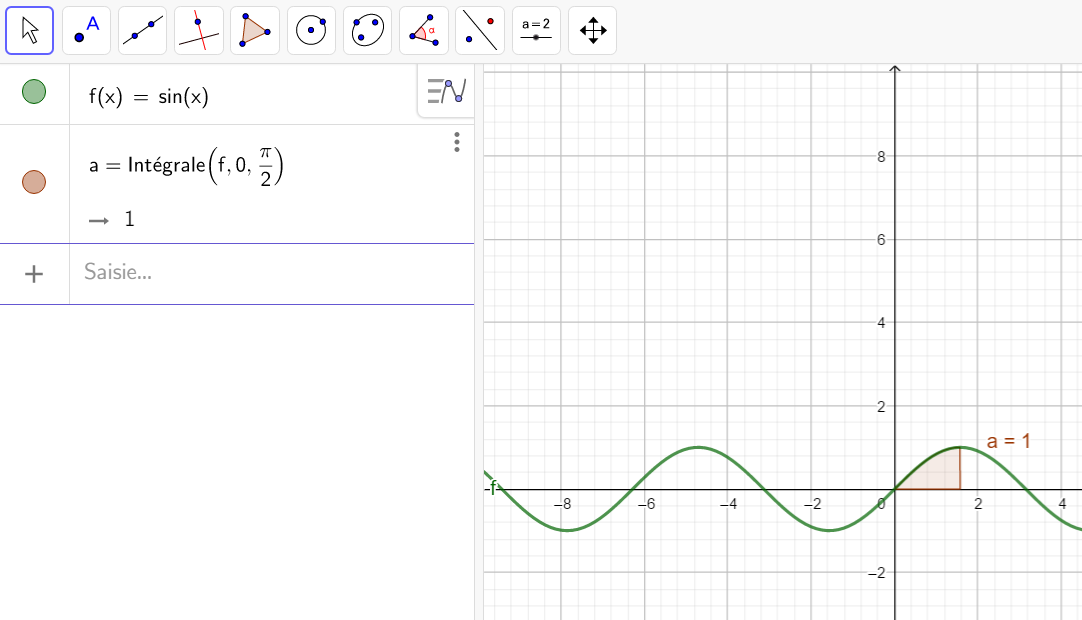
Après avoir saisi la fonction, par exemple   f(x)=\sqrt{x}.

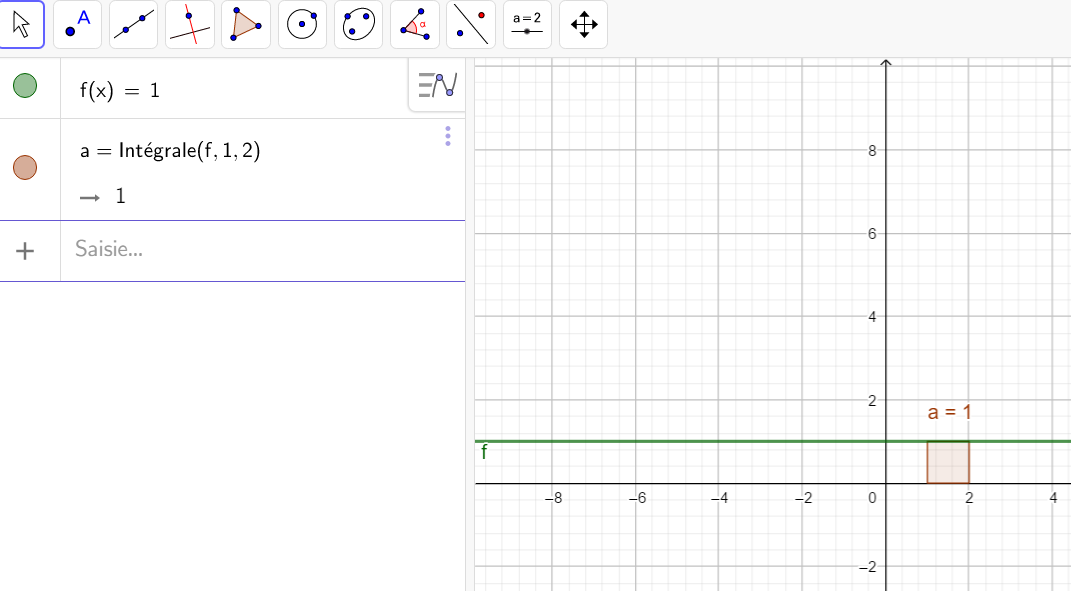
Il faut saisir en-dessous , dans la colonne Algèbre située à gauche de l’écran, intégrale(f,0,4).

La valeur de l’intégrale s’affiche dans la colonne Algèbre et l’aire correspondante apparaît en couleur dans le repère.

Exercice n°1

En utilisant, la page Géogébra ci_dessus, calculer les intégrales suivantes ( il n’est pas nécessaire de tout retaper, modifier juste ce qui doit l’être ). On a choisi des fonctions continues et positives sur leur intervalle d’intégration.

1.\int_1^4 \sqrt{x}\hspace{0.05cm}dx

correction

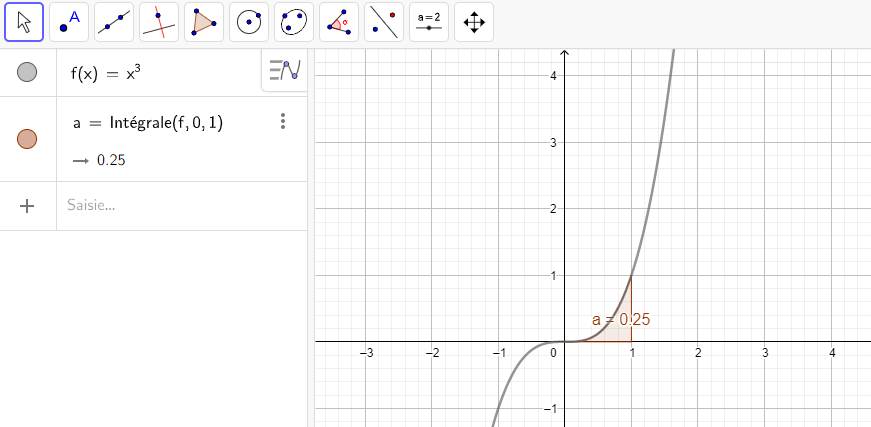
2.\int_0^1 x^3\hspace{0.05cm}dx

correction

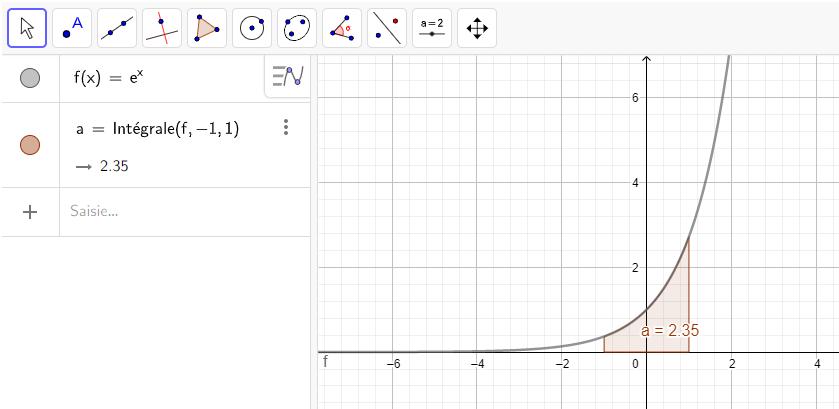
3.\int_{-1}^1 e^x\hspace{0.05cm}dx

correction

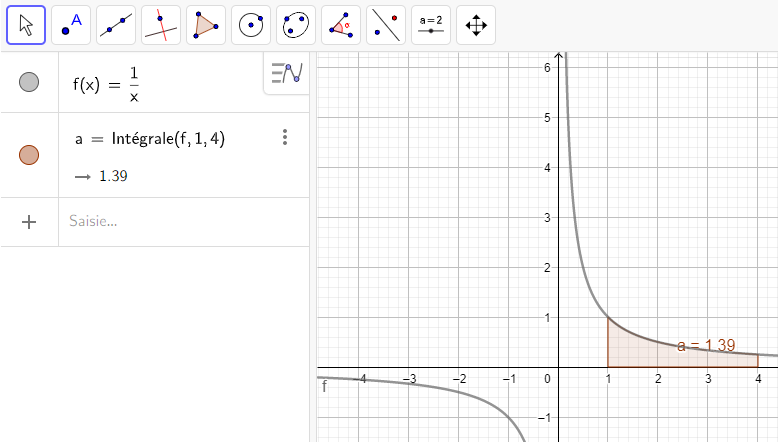
4.\int_1^4 \frac{1}{x}\hspace{0.05cm}dx

correction

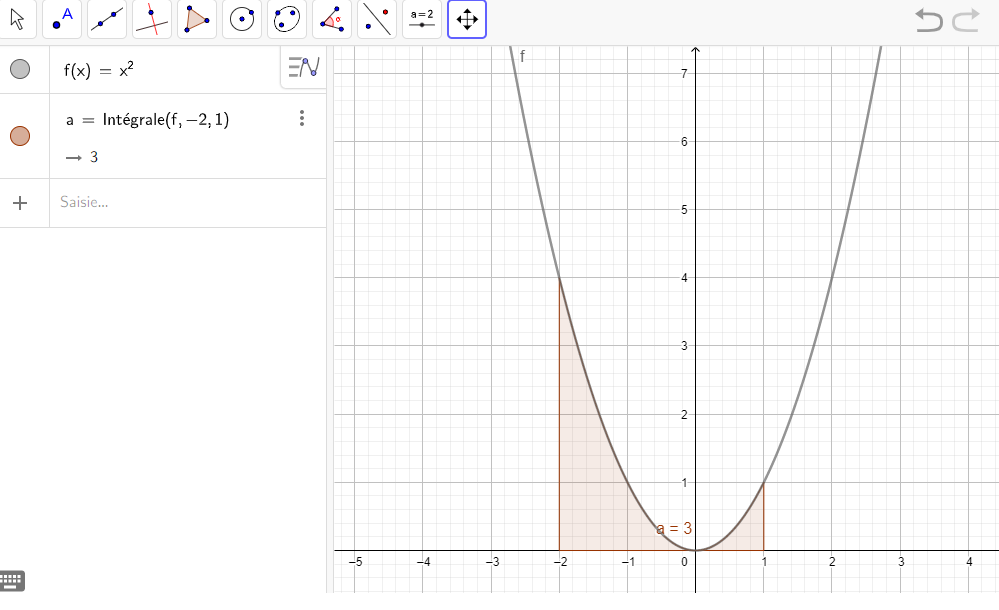
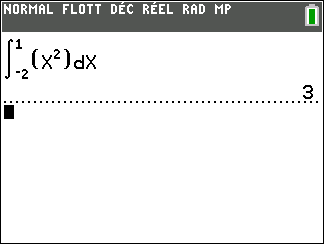
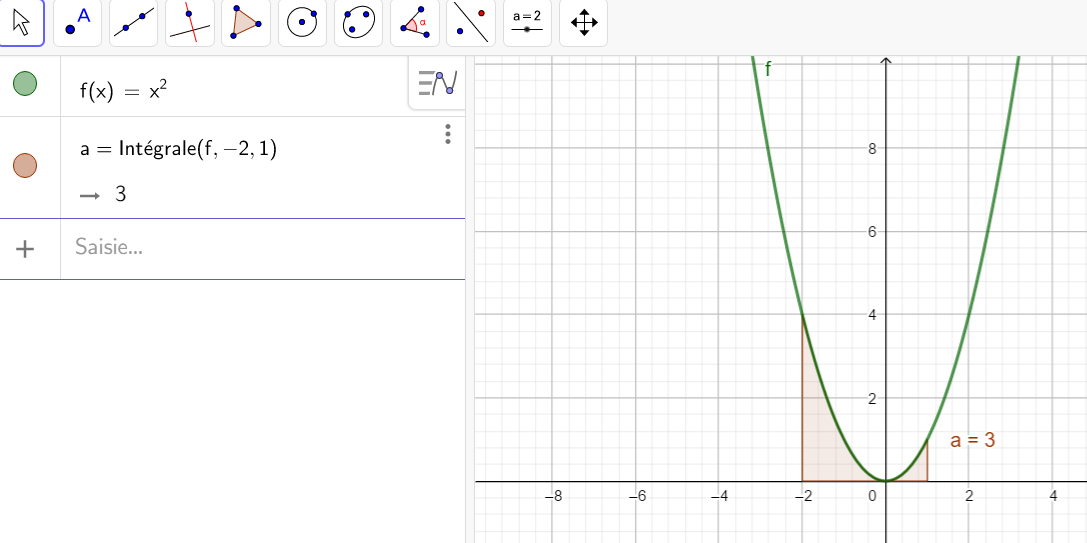
5.\int_{-2}^{1} x^2\hspace{0.05cm}dx

correction

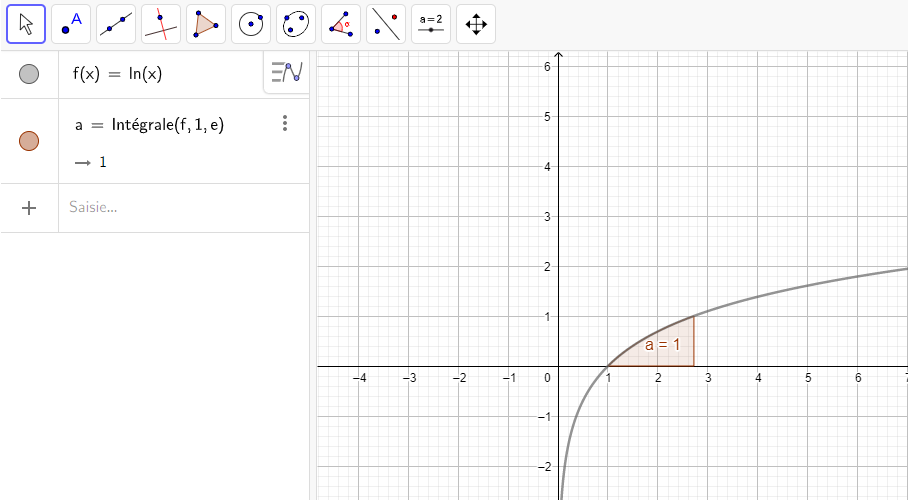
6.\int_1^e ln(x)\hspace{0.05cm}dx

correction

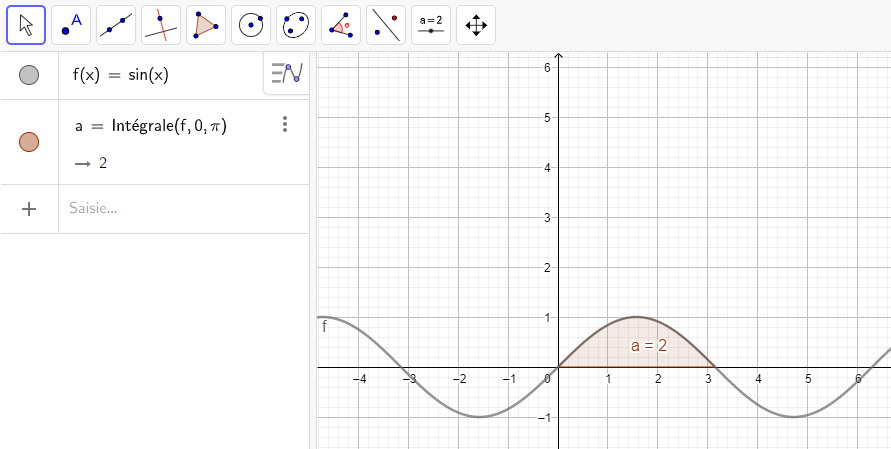
7.\int_{0}^{\pi} sin(x)\hspace{0.05cm}dx

correction

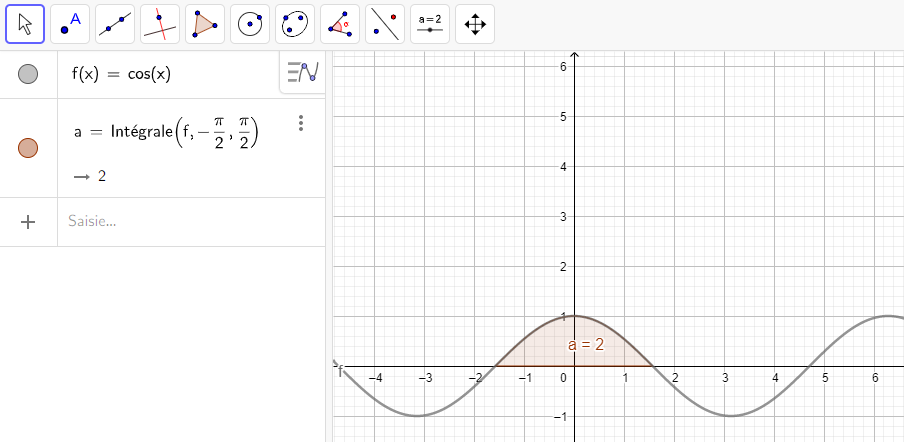
8.\int_{-\pi}^{\pi} cos(x)\hspace{0.05cm}dx

correction

Intégrale d’une fonction continue 

Théorème fondamental

Soit f une fonction continue sur un intervalle [a;b].

La fonction F_a définie sur [a;b] par F_a(x)=\int_a^x f(f)\hspace{0.05cm}dt est la primitive de f sur  [a;b] qui s’annule en a.

C’est-à-dire que pout tout x de [a;b] , F_a'(x)=f(x).

Calcul de l’intégrale d’une fonction continue 

Propriété

Soit f une fonction continue et positive sur un intervalle [a;b].

Si F est une primitive de  f alors  \int_a^b f(x)\hspace{0.05cm}dx=F(b)-F(a).

Propriété

Toute fonction continue  sur un intervalle I admet des primitives sur I.

Définition

Soit f une fonction continue sur un intervalle I , F une une primitive de  f et a et b deux réels de  I. On appelle intégrale de a à b de f le réel noté \int_a^b f(x)\hspace{0.05cm}dx=[F(x)]_a^b=F(b)-F(a).

Exercice n°2

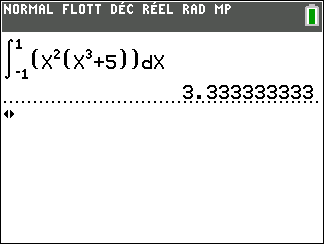
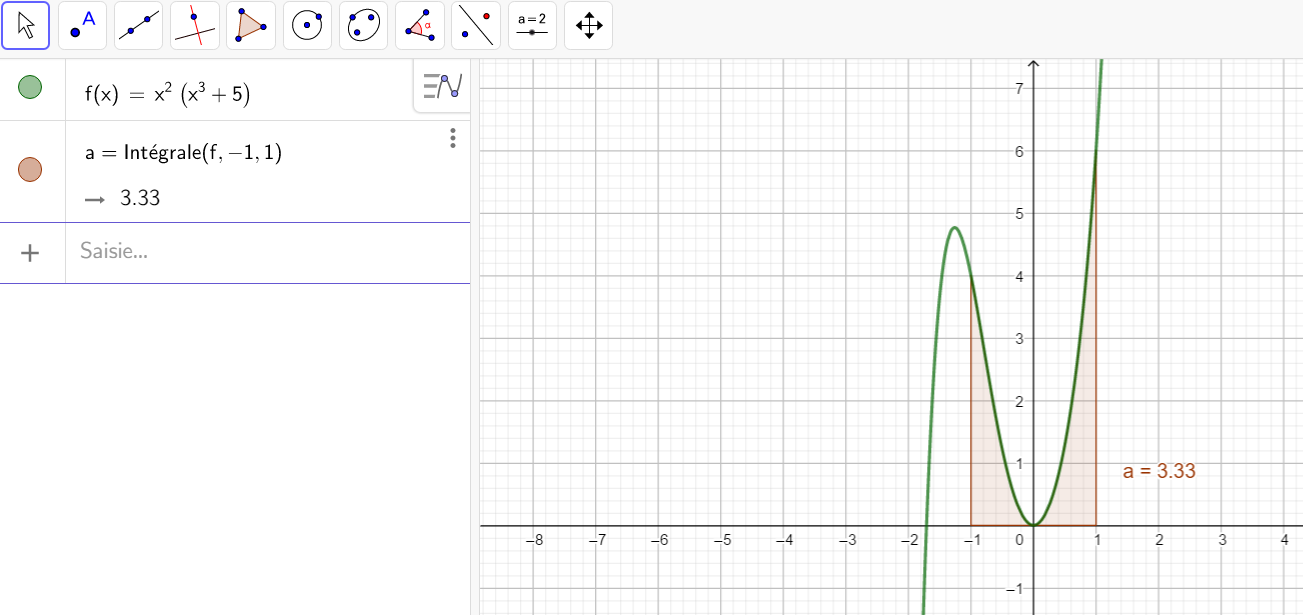
Calculer les intégrales suivantes en utilisant la définition ci-dessus.

1.\int_1^2 \hspace{0.05cm}dx

je programme ma TI 83
correction

2.\int_{-4}^4 5\hspace{0.05cm}dx

je programme ma TI 83
correction

3.\int_{-1}^1 2x+1\hspace{0.05cm}dx

je programme ma TI 83
correction

4.\int_{0}^2 (3x^2+2x)\hspace{0.05cm}dx

je programme ma TI 83
correction

5.\int_{-2}^{1} x^2\hspace{0.05cm}dx

je programme ma TI 83
correction

6.\int_0^2 e^x\hspace{0.05cm}dx

je programme ma TI 83
correction

7.\int_{0}^{\frac{\pi}{2}} sin(x)\hspace{0.05cm}dx

je programme ma TI 83
correction

8.\int_{1}^{2} -\frac{1}{x^2}\hspace{0.05cm}dx

je programme ma TI 83
correction

Exercice n°3

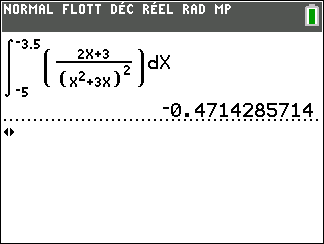
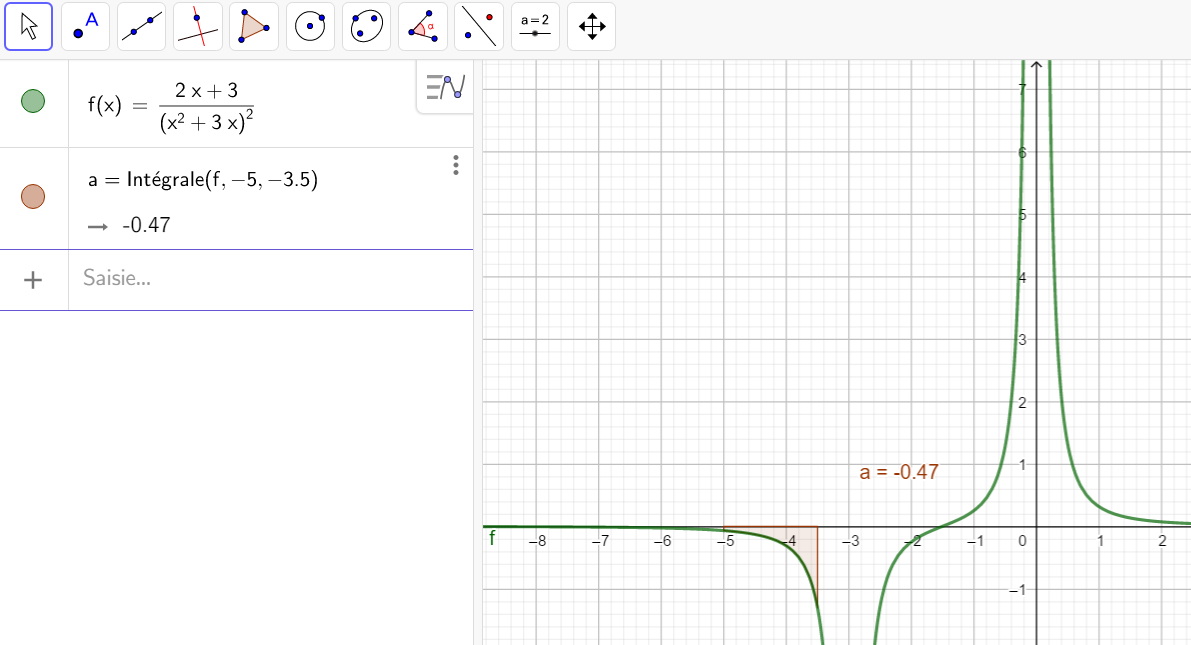
Calculer les intégrales suivantes en utilisant la définition ci-dessus.

1.\int_{-2}^0 e^x(e^x+1)^2\hspace{0.05cm}dx

je programme ma TI 83
correction

2.\int_{-1}^1x^2(x^3+5) \hspace{0.05cm}dx

je programme ma TI 83
correction

3.\int_{-5}^{-3.5} \frac{2x+3}{(x^2+3x)^2} \hspace{0.05cm}dx

je programme ma TI 83
correction

4.\int_{-3}^3 \frac{x}{(x^2+1)^2}\hspace{0.05cm}dx

je programme ma TI 83
correction

5.\int_{-2}^2 \frac{2x}{x^2+5}\hspace{0.05cm}dx

je programme ma TI 83
correction

6.\int_0^2 \frac{e^x}{e^x+1}\hspace{0.05cm}dx

je programme ma TI 83
correction

7.\int_{-1}^{1} xe^{x^2}\hspace{0.05cm}dx

je programme ma TI 83
correction

8.\int_{-1}^{2} \frac{x}{\sqrt{x^2+1}}\hspace{0.05cm}dx

je programme ma TI 83
correction

Propriétés et intégration par parties

Propriétés

Soient f et g deux fonctions continues sur un intervalle I.

a,b,c sont trois réels de l’intervalle I et k est une constante réelle.

  1. \int_{a}^a f(x)\hspace{0.05cm}dx=0

2. \int_{b}^a f(x)\hspace{0.05cm}dx=-\int_{a}^b f(x)\hspace{0.05cm}dx

3. \int_{a}^b kf(x)\hspace{0.05cm}dx=k\int_{a}^b f(x)\hspace{0.05cm}dx

4. \int_{a}^b (f(x)+g(x))\hspace{0.05cm}dx=\int_{a}^b f(x)\hspace{0.05cm}dx +\int_{a}^b g(x)\hspace{0.05cm}dx

5. \int_{a}^b f(x)\hspace{0.05cm}dx+\int_{b}^c f(x)\hspace{0.05cm}dx =\int_{a}^c f(x)\hspace{0.05cm}dx

6. Si pour tout x de [a;b], f(x)\geq 0 alors \int_{a}^b f(x)\hspace{0.05cm}dx\geq 0

7. Si pour tout x de [a;b], f(x)\geq g(x) alors \int_{a}^b f(x)\hspace{0.05cm}dx\geq \int_{a}^b g(x)\hspace{0.05cm}dx

Exercice n°4

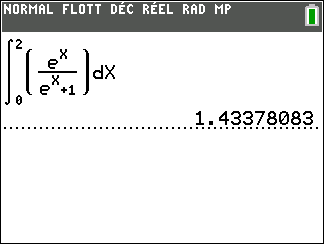
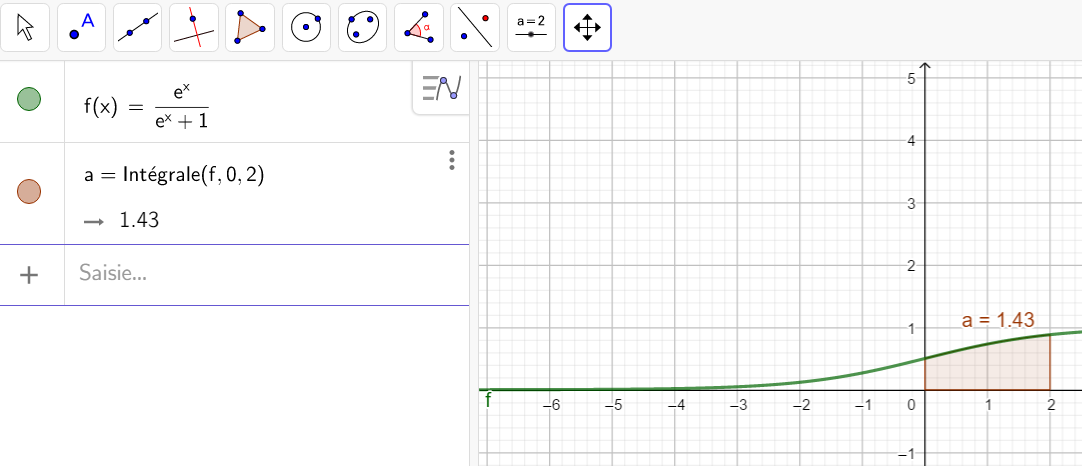
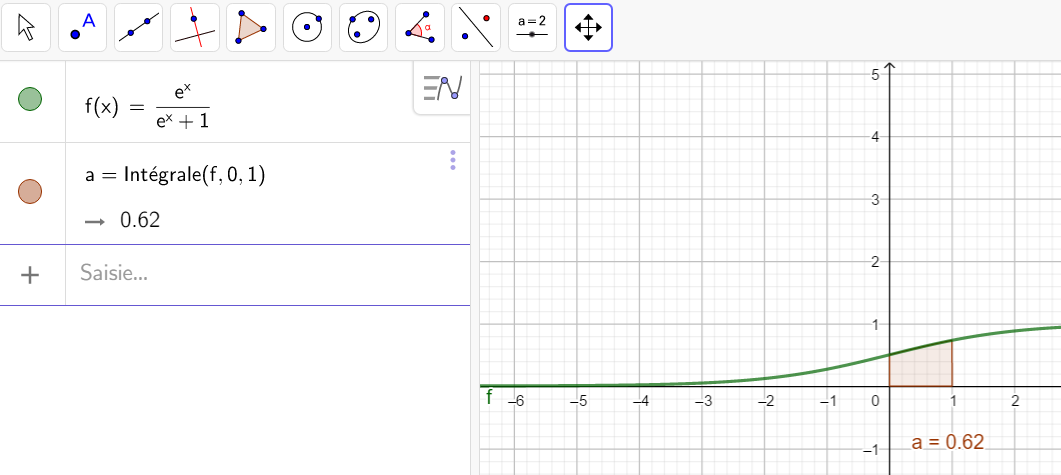
Soit I=\int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx et J=\int_{0}^1 \frac{1}{e^x+1}\hspace{0.05cm}dx

  1. Utiliser la propriété n°4 et calculer ensuite la valeur de I+J
correction

2. Calculer la valeur de I

correction

3. Déduire des questions précédentes la valeur de J.

correction

Exercice n°5

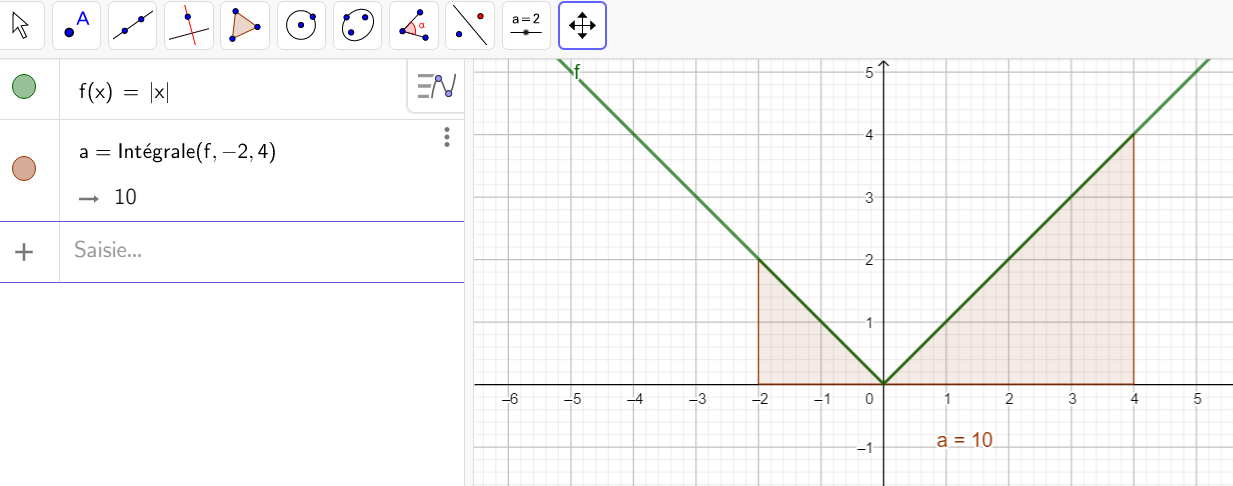
En utilisant la relation de Chasles, calculer  \int_{-2}^4 |x|\hspace{0.05cm}dx

correction

Exercice n°6

  1. Donner un encadrement de  ln(x) sur l’intervalle [1;e]
correction

2. En utilisant la propriété n°7, en déduire que  0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq \frac{e^3-1}{3} .

correction

Intégration par parties

Soient u et v deux fonctions dérivables sur un intervalle I et dont les dérivées u’ et v’ sont continues sur I .

a,b sont deux réels de l’intervalle I.

 \int_{b}^a u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{a}^b-\int_{a}^b u'(x)v(x)\hspace{0.05cm}dx

Exercice n°7

Calculer les intégrales suivantes à l’aide d’une intégration par parties..

1.\int_{1}^e xln(x)\hspace{0.05cm}dx

correction

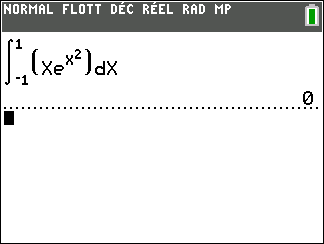
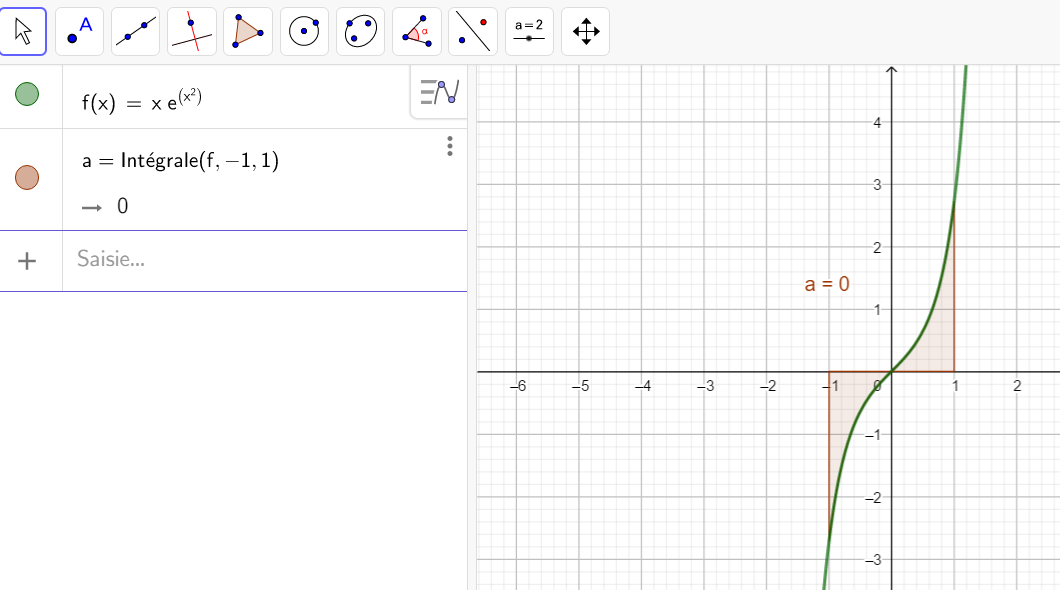
2.\int_{0}^1xe^x \hspace{0.05cm}dx

correction

3.\int_{0}^{\frac{\pi} {3}}(x-1)cos(x) \hspace{0.05cm}dx

correction

4.\int_{1}^e ln(x)\hspace{0.05cm}dx

correction

Applications du calcul intégral

Calculs d’aires

Cas n°1 : f est positive sur [a;b].

L’aire limitée par x=a , x=b , C_f et l’axe des abscisses est \int_{a}^b f(x)\hspace{0.05cm}dx

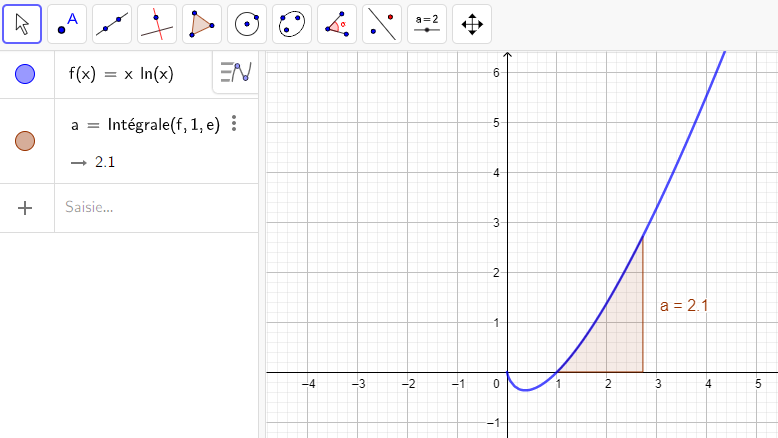
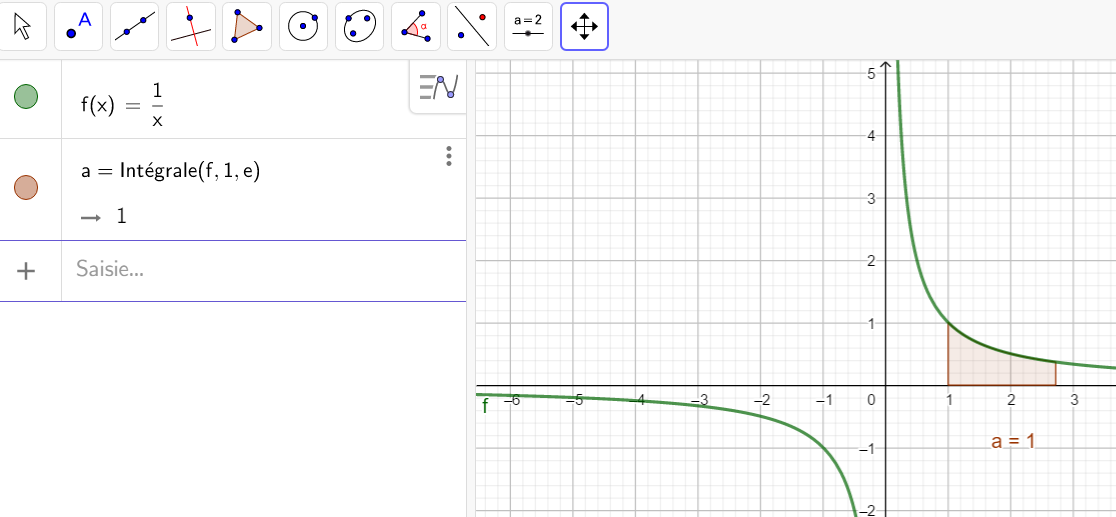
Exemple n°1 :

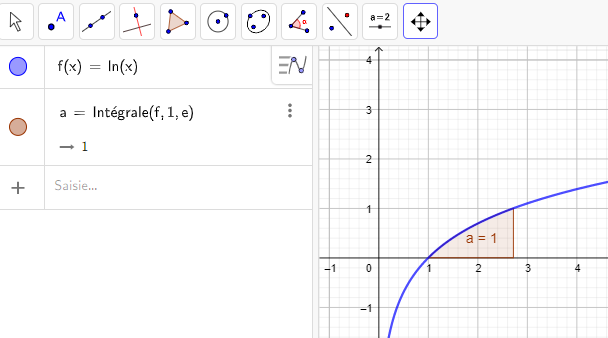
L’aire limitée par x=1 , x=e , C_f et l’axe des abscisses est \int_{1}^e f(x)\hspace{0.05cm}dx=1

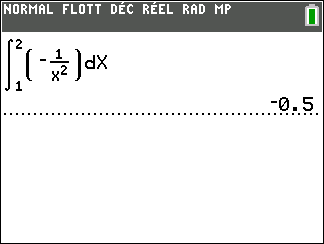
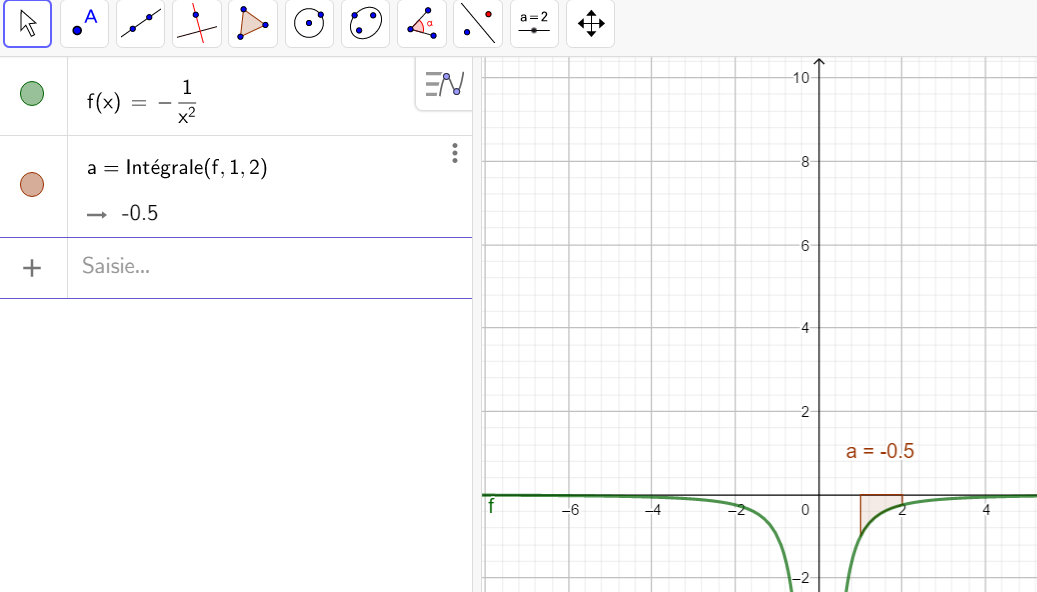
Cas n°2 : f est négative sur [a;b].

L’aire limitée par x=a , x=b , C_f et l’axe des abscisses est -\int_{a}^b f(x)\hspace{0.05cm}dx

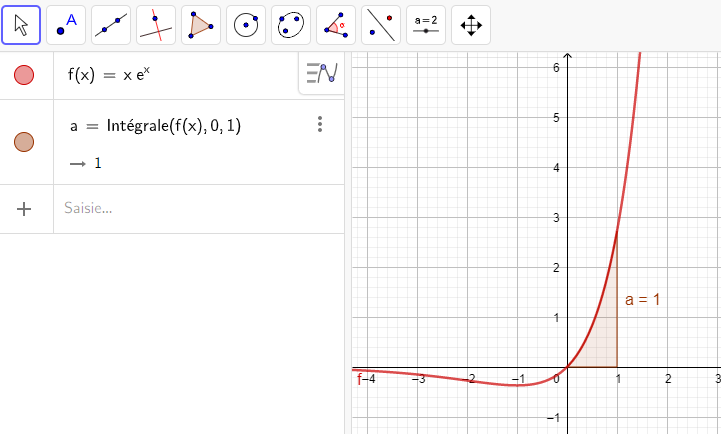
Exemple n°2 :

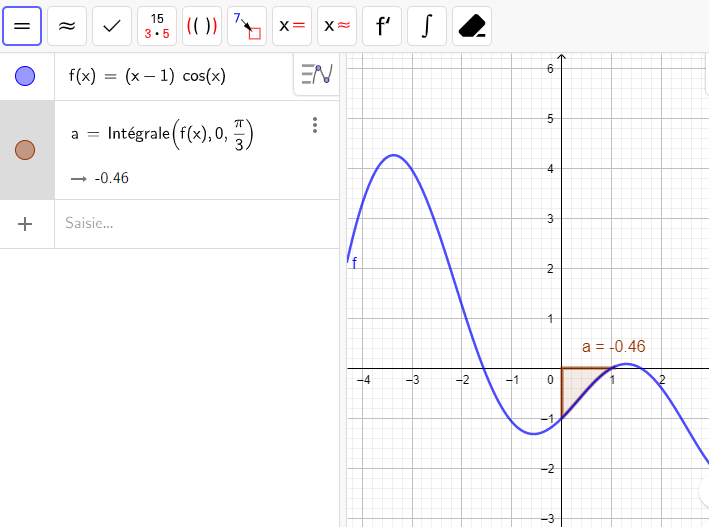
L’aire limitée par x=0 , x=\frac{\pi}{3} , C_f et l’axe des abscisses est -\int_{0}^{\frac{\pi}{3}} f(x)\hspace{0.05cm}dx=-(-0.46)

Cas n°3: f change de signe sur [a;b].

On utilise la relation de Chasles et ce qu’on a vu dans les cas 1 et 2 pour calculer l’aire limitée par x=a , x=b , C_f et l’axe des abscisses. 

Exemple n°3 :

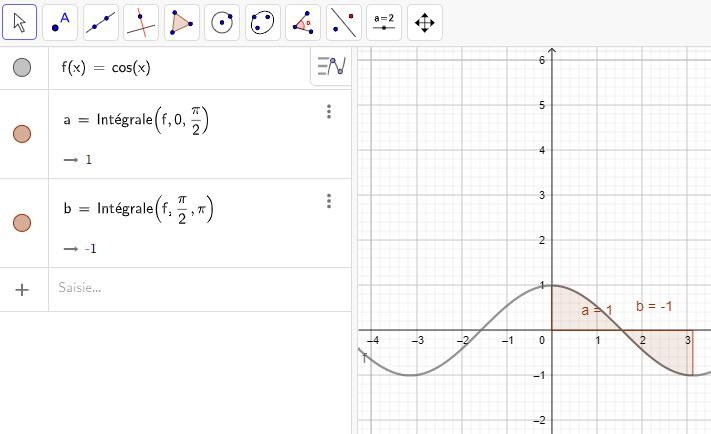
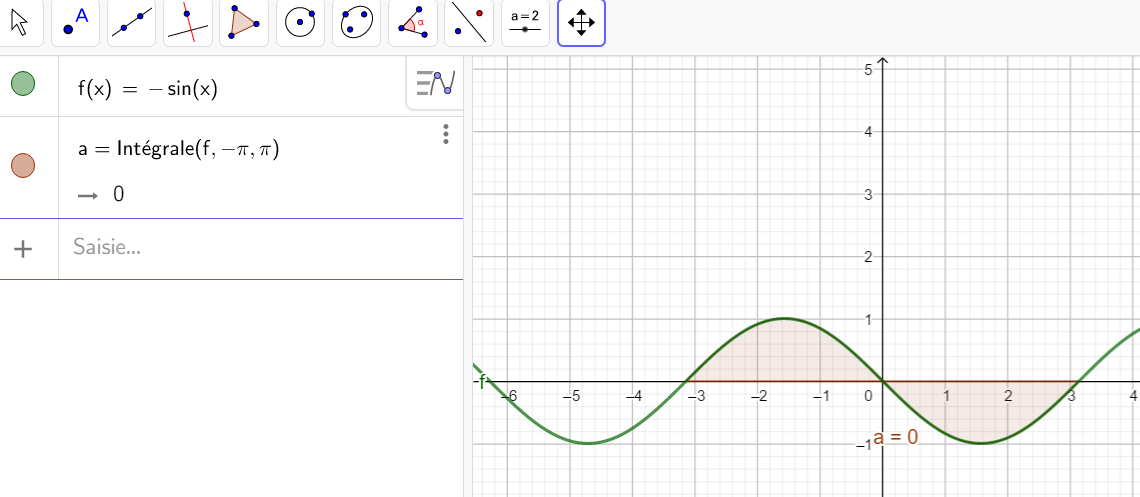
L’aire limitée par x=0 , x=\pi , C_f et l’axe des abscisses est \int_{0}^{\frac{\pi}{2}} f(x)\hspace{0.05cm}dx–\int_{\frac{\pi}{2}}^{\pi} f(x)\hspace{0.05cm}dx=1-(-1)=2

Exercice n°8

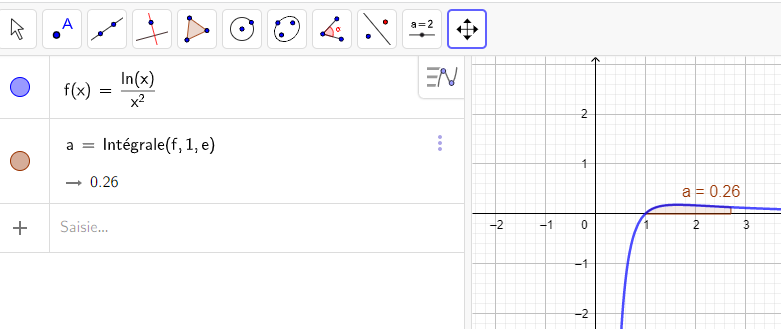
Soit f une fonction définie sur ]0;+\infty[  par f(x)=\frac{ln(x)}{x^2}. 

Calculer, en unités d’aire, l’aire du domaine compris  entre la courbe  C_f , l’axe des abscisses et les droites d’équations respectives x=1 et x=e. 

On utilisera une intégration par parties.

correction

Exercice n°9

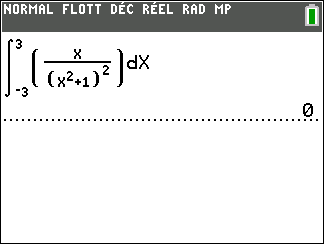
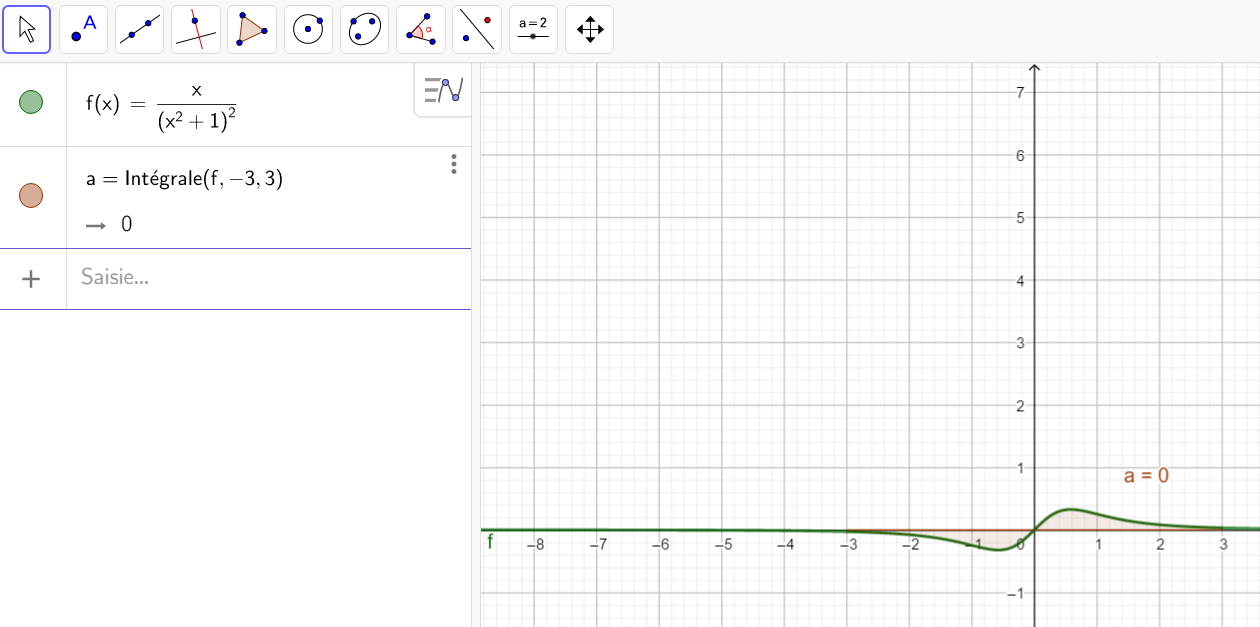
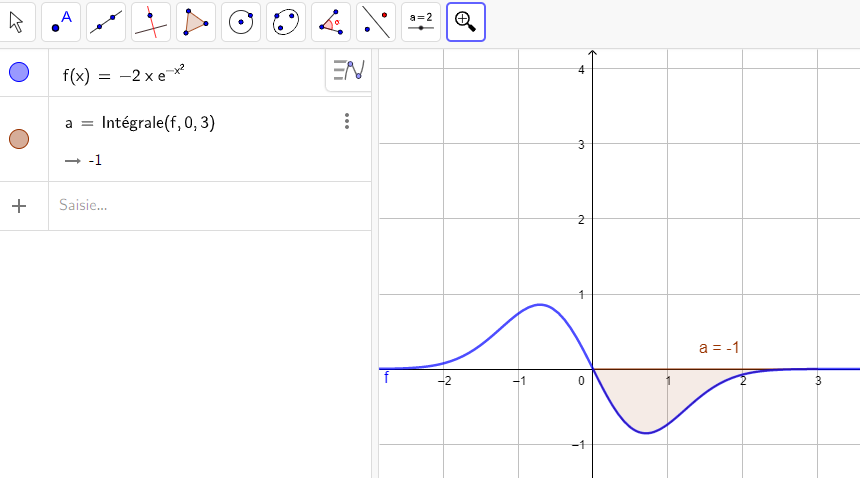
Soit f une fonction définie sur \mathbf{R}  par f(x)=-2xe^{-x^2}. 

Calculer, en unités d’aire, l’aire du domaine compris  entre la courbe  C_f , l’axe des abscisses et les droites d’équations respectives x=0 et x=3. 

correction

Propriété

Soient f et g deux fonctions continues sur un intervalle I telles que f(x)\leq g(x)

Soient deux réels a et b de l’intervalle I tels que a<b.

L’aire ( en unités d’aire) de la partie du plan limitée par x=a , x=b , C_f et C_g est égale à :

  \int_{a}^b (g(x)-f(x))\hspace{0.05cm}dx

Exercice n°10

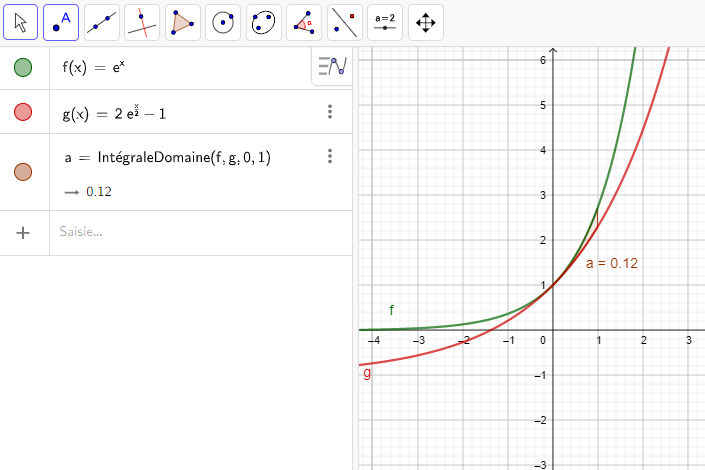
Soient f et g les fonctions définies sur \mathbf{R}  par
f(x)=e^x et g(x)=2e^{\frac{x}{2}}-1.

On admet que f(x)\geq g(x) Calculer, en unité d’aire, l’aire du domaine compris entre les courbes ) Calculer, en unité d’aire, l’aire du domaine compris entre les courbes C_f et C_g et les droites d’équations respectives x=0 et x=1. 

correction

Valeur moyenne d’une fonction

Propriété

Soit f une fonction continue sur un intervalle [a;b].

On appelle valeur moyenne de f sur [a;b] le réel suivant :

  \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx

Exercice n°11

Calculer la valeur moyenne de f sur l’intervalle proposé

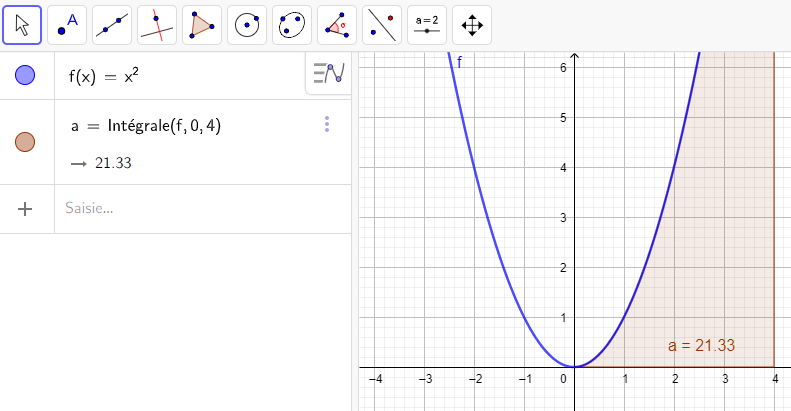
1.f(x)=x^2 sur l’intervalle [0;4]

correction

2.f(x)=\frac{1}{x} sur l’intervalle [1;e]

correction

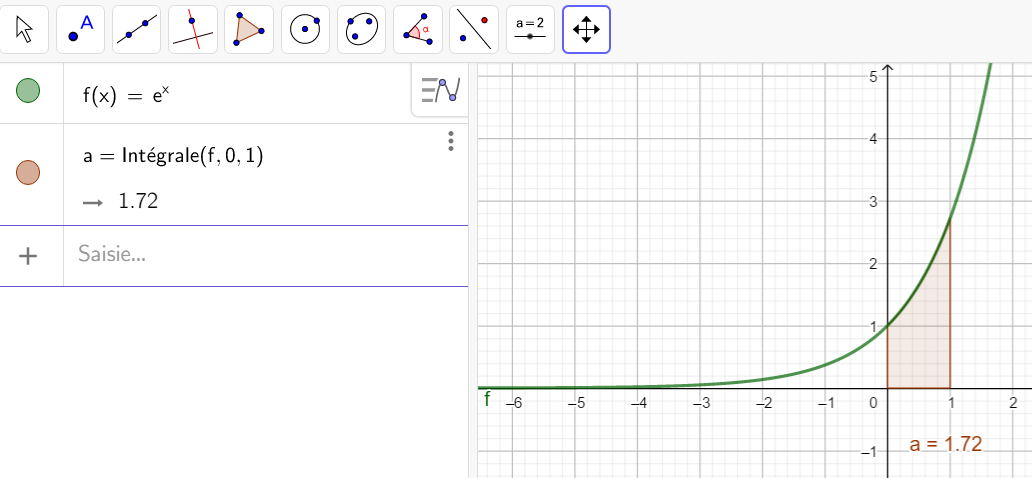
3.f(x)=e^x sur l’intervalle [0;1].

correction

4.f(x)=-sin(x) sur l’intervalle [-\pi;\pi].

correction

©2020 – Math’O karé SAS

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_1^2 \hspace{0.05cm}dx.

Ensuite on va calculer \int_1^2 \hspace{0.05cm}dx. Comme il n’y a pas de fonction visible, on peut modifier l’écriture ainsi : \int_1^21 \hspace{0.05cm}dx

1.Calcul d’une primitive de la fonction x\to 1.

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=1.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=k est F(x)=kx.

Une primitive de f(x)=1 est F(x)=1\times x

Une primitive de f(x)=1 est F(x)=x

2.Calcul de l’intégrale.

\int_1^21\hspace{0.05cm}dx=[F(x)]_1^2\\\hspace{1.15cm}=F(2)-F(1)\\\hspace{1.15cm}=2-1\\\hspace{1.15cm}=1

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-4}^4 5\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-4}^4 5\hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to 5.

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=5.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=k est F(x)=kx.

Une primitive de f(x)=5 est F(x)=5x.

2.Calcul de l’intégrale.

\int_{-4}^45\hspace{0.05cm}dx=[F(x)]_{-4}^4\\\hspace{1.15cm}=F(4)-F(-4)\\\hspace{1.15cm}=5\times 4-5\times(-4)\\\hspace{1.15cm}=20-(-20)\\\hspace{1.15cm}=20+20\\\hspace{1.15cm}=40

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-1}^1 2x+1\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-1}^1 (2x+1)\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to 2x+1.

La fonction est la somme de deux termes 2x et 1. A l’aide du tableau ci-dessous on cherche des primitives de 2x et 1.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de x est \frac{x^2}{2}.

Une primitive de 2x est 2\times \frac{x^2}{2}

Une primitive de 2x est x^2.

Une primitive de 1 est x.

Une primitive d’une somme est la somme des primitives, donc :

F(x)=x^2+x

2.Calcul de l’intégrale.

\int_{-1}^1(2x+1)\hspace{0.05cm}dx=[F(x)]_{-1}^1\\\hspace{2.3cm}=F(1)-F(-1)\\\hspace{2.3cm}=(1^2+1)-((-1)^2+(-1))\\\hspace{2.3cm}=(1+1)-(1-1)\\\hspace{2.3cm}=2-0\\\hspace{2.3cm}=2

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_0^2(3x^2+2x)\hspace{0.05cm}dx.

Ensuite on va calculer \int_0^2(3x^2+2x)\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to 3x^2+2x.

La fonction est la somme de deux termes 3x^2 et 2x. A l’aide du tableau ci-dessous on cherche des primitives de 3x^2 et 2x.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de x^2 est \frac{x^3}{3}.

Une primitive de 3x^2 est 3\times \frac{x^3}{3}

Une primitive de 3x^2 est x^3

Une primitive de x est \frac{x^2}{2}.

Une primitive de 2x est 2\times \frac{x^2}{2}

Une primitive de 2x est x^2.

Une primitive d’une somme est la somme des primitives, donc :

F(x)=x^3+x^2

2.Calcul de l’intégrale.

\int_0^2(3x^2+2x)\hspace{0.05cm}dx=[F(x)]_0^2\\\hspace{2.5cm}=F(2)-F(0)\\\hspace{2.5cm}=(2^3+2^2)-(0^3+0^2)\\\hspace{2.5cm}=8+4-0\\\hspace{2.5cm}=12

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-2}^{1} x^2\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-2}^{1} x^2\hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to x^2.

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=x^2.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=x^2 est F(x)=\frac{x^3}{3}.

2.Calcul de l’intégrale.

\int_{-2}^{1} x^2\hspace{0.05cm}dx=[F(x)]_{-2}^{1}\\\hspace{1.45cm}=F(1)-F(-2)\\\hspace{1.45cm}=\frac{1^3}{3}-\frac{(-2)^3}{3}\\\hspace{1.45cm}=\frac{1}{3}-\frac{-8}{3}\\\hspace{1.45cm}=\frac{1}{3}+\frac{8}{3}\\\hspace{1.45cm}=\frac{9}{3}\\\hspace{1.45cm}=3

 

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_0^2 e^x\hspace{0.05cm}dx.

Ensuite on va calculer \int_0^2 e^x\hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to e^x.

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=e^x.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=e^x est F(x)=e^x.

2.Calcul de l’intégrale.

\int_0^2 e^x\hspace{0.05cm}dx=[F(x)]_{0}^2\\\hspace{1.15cm}=F(2)-F(0)\\\hspace{1.15cm}=e^2-e^0\\\hspace{1.15cm}=e^2-1

Comme e^2-1\approx 6.39, en comparant avec Géogébra, on valide la réponse. 

 

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^{\frac{\pi}{2}} sin(x)\hspace{0.05cm}dx.

Ensuite on va calculer \int_{0}^{\frac{\pi}{2}} sin(x)\hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to sin(x).

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=sin(x).

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=sin(x) est F(x)=-cos(x).

2.Calcul de l’intégrale.

\int_{0}^{\frac{\pi}{2}} sin(x)\hspace{0.05cm}dx=[F(x)]_{0}^{\frac{\pi}{2}}\\\hspace{1.15cm}=F(\frac{\pi}{2})-F(0)\\\hspace{1.15cm}=-cos(\frac{\pi}{2})-(-cos(0))\\\hspace{1.15cm}=0-(-1)\\\hspace{1.15cm}=1

 

 

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche \frac{\Box}{\Box}.

 

Valider par entrer.

Complèter les cadres puis valider par entrer.

On peut utiliser Géogébra pour conjecturer la valeur de \int_{1}^{2} -\frac{1}{x^2}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{1}^{2} -\frac{1}{x^2}\hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to -\frac{1}{x^2}.

La fonction est une fonction de référence. A l’aide du tableau ci-dessous on cherche une primitive de f(x)=-\frac{1}{x^2}.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de f(x)=-\frac{1}{x^2} est F(x)=\frac{1}{x}.

2.Calcul de l’intégrale.

\int_{1}^{2} -\frac{1}{x^2}\hspace{0.05cm}dx=[F(x)]_{1}^2\\\hspace{1.15cm}=F(2)-F(1)\\\hspace{1.15cm}=\frac{1}{2}-\frac{1}{1}\\\hspace{1.15cm}=\frac{1}{2}-1\\\hspace{1.15cm}=-\frac{1}{2}

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-2}^0e^x(e^x+1)^2 \hspace{0.05cm}dx.

Ensuite on va calculer \int_{-2}^0e^x(e^x+1)^2 \hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to e^x(e^x+1)^2.

On cherche de quelle forme est la fonction f(x)=e^x(e^x+1)^2 pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=e^x(e^x+1) est de la forme u'(x)\times u^n(x) avec u(x)= e^x+1 et n= 2.

1.Je calcule u'(x)

u'(x)= (e^x+1)’

u'(x)= (e^x)’+(1)’

u'(x)= e^x+0

u'(x)=e^x

2.Je remplace u(x) par e^x+1, u'(x) par e^x  et n par 2 dans la formule ci-dessous :

u'(x)\times u^n(x) a pour primitive \frac{u^{n+1}(x)}{n+1}.

e^x\times (e^x+1)^2 a pour primitive \frac{(e^x+1)^{2+1}}{2+1}\\e^x\times (e^x+1)^2 a pour primitive \frac{(e^x+1)^{3}}{3}

Donc F(x)=\frac{(e^x+1)^{3}}{3}

2.Calcul de l’intégrale.

\int_{-2}^0 e^x(e^x+1)^2 \hspace{0.05cm}dx=[F(x)]_{-2}^0\\\hspace{2.65cm}=F(0)-F(-2)\\\hspace{2.65cm}=\frac{(e^0+1)^{3}}{3}-\frac{(e^{-2}+1)^{3}}{3}\\\hspace{2.65cm}=\frac{(1+1)^{3}}{3}-\frac{(e^{-2}+1)^{3}}{3}\\\hspace{2.65cm}=\frac{(2)^{3}}{3}-\frac{(e^{-2}+1)^{3}}{3}\\\hspace{2.65cm}=\frac{8}{3}-\frac{(e^{-2}+1)^{3}}{3}

Comme \frac{8}{3}-\frac{(e^{-2}+1)^{3}}{3}\approx 2.18, en comparant avec Géogébra, on valide la réponse. 

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-1}^1x^2(x^3+5) \hspace{0.05cm}dx.

Ensuite on va calculer \int_{-1}^1x^2(x^3+5) \hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to x^2(x^3+5).

On cherche de quelle forme est la fonction f(x)=x^2(x^3+5) pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=x^2(x^3+5) est de la forme u'(x)\times u^n(x) avec u(x)= x^3+5 et n= 1.

1.Je calcule u'(x)

u'(x)= (x^3+5)’

u'(x)= (x^3)’+(5)’

u'(x)= 3x^2+0

u'(x)= 3x^2

2.Je remplace u(x) par x^3+5, u'(x) par 3x^2 et n par 1 dans la formule ci-dessous :

u'(x)\times u^n(x) a pour primitive \frac{u^{n+1}(x)}{n+1}.

3x^2\times (x^3+5) a pour primitive \frac{(x^3+5)^2}{1+1}\\3x^2(x^3+5) a pour primitive \frac{(x^3+5)^2}{2}

Pour obtenir x^2(x^3+5), c’est-à-dire f(x) à gauche, on peut diviser par 3 de chaque côté.

x^2(x^3+5) a pour primitive \frac{(x^3+5)^2}{6}

Donc F(x)=\frac{(x^3+5)^2}{6}

2.Calcul de l’intégrale.

\int_{-1}^1x^2(x^3+5) \hspace{0.05cm}dx=[F(x)]_{-1}^1\\\hspace{2.65cm}=F(1)-F(-1)\\\hspace{2.65cm}=\frac{(1^3+5)^2}{6}-\frac{((-1)^3+5)^2}{6}\\\hspace{2.65cm}=\frac{(1+5)^2}{6}-\frac{(-1+5)^2}{6}\\\hspace{2.65cm}=\frac{6^2}{6}-\frac{4^2}{6}\\\hspace{2.65cm}=\frac{6^2}{6}-\frac{16}{6}\\\hspace{2.65cm}=6-\frac{8}{3}\\\hspace{2.65cm}=6\times \frac{3}{3}-\frac{8}{3}\\\hspace{2.65cm}= \frac{18}{3}-\frac{8}{3}\\\hspace{2.65cm}= \frac{10}{3}

Comme \frac{10}{3}\approx 3.33, en comparant avec Géogébra, on valide la réponse. 

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-5}^{-3.5} \frac{2x+3}{(x^2+3x)^2} \hspace{0.05cm}dx.

Ensuite on va calculer \int_{-5}^{-3.5} \frac{2x+3}{(x^2+3x)^2} \hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to \frac{2x+3}{(x^2+3x)^2}.

On cherche de quelle forme est la fonction f(x)=\frac{2x+3}{(x^2+3x)^2} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{2x+3}{(x^2+3x)^2} est de la forme \frac{u'(x)}{u^2(x)} avec u(x)= x^2+3x.

1.Je calcule u'(x)

u'(x)= (x^2+3x)’

u'(x)= (x^2)’+(3x)’

u'(x)= 2x+3

2.Je remplace u(x) par x^2+3x et u'(x) par 2x+3  dans la formule ci-dessous :

\frac{u'(x)}{u^2(x)} a pour primitive -\frac{1}{u(x)}

\frac{2x+3}{(x^2+3x)^2} a pour primitive -\frac{1}{x^2+3x}

Donc F(x)=-\frac{1}{x^2+3x}

2.Calcul de l’intégrale.

\int_{-5}^{-3.5} \frac{2x+3}{(x^2+3x)^2} \hspace{0.05cm}dx=[F(x)]_{-5}^{-3.5}\\\hspace{2.65cm}=F(-3.5)-F(-5)\\\hspace{2.65cm}=-\frac{1}{(-3.5)^2+3\times (-3.5)}-(-\frac{1}{(-5)^2+3\times (-5)})\\\hspace{2.65cm}=-\frac{1}{12.25-10.5}+\frac{1}{25-15}\\\hspace{2.65cm}=-\frac{1}{1.75}+\frac{1}{10}\\\hspace{2.65cm}=-0.47

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-3}^{3} \frac{x}{(x^2+1)^2} \hspace{0.05cm}dx.

Ensuite on va calculer \int_{-3}^{3} \frac{x}{(x^2+1)^2} \hspace{0.05cm}dx. 

1.Calcul d’une primitive de la fonction x\to \frac{x}{(x^2+1)^2}.

On cherche de quelle forme est la fonction f(x)=\frac{x}{(x^2+1)^2} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{x}{(x^2+1)^2} est de la forme \frac{u'(x)}{u^2(x)} avec u(x)= x^2+1.

1.Je calcule u'(x)

u'(x)= (x^2+1)’

u'(x)= (x^2)’+(1)’

u'(x)= 2x+0

u'(x)= 2x

2.Je remplace u(x) par x^2+1 et u'(x) par 2x  dans la formule ci-dessous :

\frac{u'(x)}{u^2(x)} a pour primitive -\frac{1}{u(x)}

\frac{2x}{(x^2+1)^2} a pour primitive -\frac{1}{x^2+1}

Pour retomber sur f(x)=\frac{x}{(x^2+1)^2} à gauche, il faut diviser par 2.

\frac{x}{(x^2+1)^2} a pour primitive -\frac{1}{2(x^2+1)}

Donc F(x)=-\frac{1}{2(x^2+1)}

2.Calcul de l’intégrale.

\int_{-3}^{3} \frac{x}{(x^2+1)^2} \hspace{0.05cm}dx=[F(x)]_{-3}^{3}\\\hspace{2cm}=F(3)-F(-3)\\\hspace{2cm}=-\frac{1}{2(3^2+1)}-(-\frac{1}{2((-3)^2+1)})\\\hspace{2cm}=-\frac{1}{2(9+1)}-(-\frac{1}{2(9+1)})\\\hspace{2cm}=-\frac{1}{2\times 10}-(-\frac{1}{2\times 10})\\\hspace{2cm}=-\frac{1}{20}+\frac{1}{20}\\\hspace{2cm}=0

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-2}^2 \frac{2x}{x^2+5}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-2}^2 \frac{2x}{x^2+5}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to \frac{2x}{x^2+5}.

On cherche de quelle forme est la fonction f(x)=\frac{2x}{(x^2+5)} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{2x}{x^2+5} est de la forme \frac{u'(x)}{u(x)} avec u(x)= x^2+5.

1.Je calcule u'(x)

u'(x)= (x^2+5)’

u'(x)= (x^2)’+(5)’

u'(x)= 2x+0

u'(x)= 2x

2.Je remplace u(x) par x^2+5 et u'(x) par 2x dans la formule ci-dessous :

\frac{u'(x)}{u(x)} a pour primitive ln|u(x)|.

\frac{2x}{x^2+5} a pour primitive ln(|x^2+5|)

Comme x^2+5 est positif, |x^2+5|=x^2+5

Donc F(x)=ln(x^2+5)

2.Calcul de l’intégrale.

\int_{-2}^{2} \frac{2x}{(x^2+5)^2} \hspace{0.05cm}dx=[F(x)]_{-2}^{2}\\\hspace{2cm}=F(2)-F(-2)\\\hspace{2cm}=ln(2^2+5)-ln((-2)^2+5)\\\hspace{2cm}=ln(4+5)-ln(4+5)\\\hspace{2cm}=ln(9)-ln(9)\\\hspace{2cm}=0

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^2 \frac{e^x}{e^x+1}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{0}^2 \frac{e^x}{e^x+1}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to \frac{e^x}{e^x+1}.

On cherche de quelle forme est la fonction f(x)=\frac{e^x}{e^x+1} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{e^x}{e^x+1}  est de la forme \frac{u'(x)}{u(x)} avec u(x)= e^x+1.

1.Je calcule u'(x)

u'(x)= (e^x+1)’

u'(x)= (e^x)’+(1)’

u'(x)= e^x+0

u'(x)= e^x

2.Je remplace u(x) par e^x+1 et u'(x) par e^x dans la formule ci-dessous :

\frac{u'(x)}{u(x)} a pour primitive ln(|u(x)|).

\frac{e^x}{e^x+1} a pour primitive ln(|e^x+1|)

e^x+1 est toujours positif donc |e^x+1|=e^x+1

Donc F(x)=ln(e^x+1)

2.Calcul de l’intégrale.

\int_{0}^2 \frac{e^x}{e^x+1}\hspace{0.05cm}dx=[F(x)]_{0}^{2}\\\hspace{1.6cm}=F(2)-F(0)\\\hspace{1.6cm}=ln(e^2+1)-ln(e^0+1)\\\hspace{1.6cm}=ln(e^2+1)-ln(1+1)\\\hspace{1.6cm}=ln(e^2+1)-ln(2)\\\hspace{1.6cm}=ln(\frac{e^2+1}{2})

Comme ln(\frac{e^2+1}{2})\approx 1.43, la conjecture précédente faite avec Géogébra permet de valider la réponse.

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-1}^1 xe^{x^2}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-1}^1 xe^{x^2}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to xe^{x^2}.

On cherche de quelle forme est la fonction f(x)=xe^{x^2} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=xe^{x^2} est de la forme u'(x)e^{u(x)} avec u(x)= x^2.

1.Je calcule u'(x)

u'(x)= (x^2)’

u'(x)= 2x

2.Je remplace u(x) par x^2 et u'(x) par 2x dans la formule ci-dessous :

u'(x)e^{u(x)} a pour primitive e^{u(x)}.

2xe^{x^2} a pour primitive e^{x^2}

Pour retrouver f(x)=xe^{x^2} à gauche, il faut diviser par 2.

xe^{x^2} a pour primitive \frac{e^{x^2}}{2}

Donc F(x)=\frac{e^{x^2}}{2}

2.Calcul de l’intégrale.

\int_{-1}^1 xe^{x^2}\hspace{0.05cm}dx=[F(x)]_{-1}^1\\\hspace{1.7cm}=F(1)-F(-1)\\\hspace{1.7cm}=\frac{e^{1^2}}{2}-\frac{e^{(-1)^2}}{2}\\\hspace{1.7cm}=\frac{e^{1}}{2}-\frac{e^{1}}{2}\\\hspace{1.7cm}=0

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-1}^2 \frac{x}{\sqrt{x^2+1}}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-1}^2 \frac{x}{\sqrt{x^2+1}}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to \frac{x}{\sqrt{x^2+1}}.

On cherche de quelle forme est la fonction f(x)=xe^{x^2} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{x}{x^2+1} est de la forme \frac{u'(x)}{2\sqrt{u(x)}} avec u(x)= x^2+1.

1.Je calcule u'(x)

u'(x)= (x^2+1)’

u'(x)= (x^2)’+(1)’

u'(x)= 2x+0

u'(x)= 2x

2.Je remplace u(x) par x^2+1 et u'(x) par 2x dans la formule ci-dessous :

\frac{u'(x)}{2\sqrt{u(x)}} a pour primitive \sqrt{u(x)}.

\frac{2x}{2\sqrt{x^2+1}} a pour primitive \sqrt{x^2+1}\\\frac{x}{\sqrt{x^2+1}} a pour primitive \sqrt{x^2+1}

Donc F(x)=\sqrt{x^2+1}

2.Calcul de l’intégrale.

\int_{-1}^2 \frac{x}{\sqrt{x^2+1}}\hspace{0.05cm}dx=[F(x)]_{-1}^2\\\hspace{1.9cm}=F(2)-F(-1)\\\hspace{1.9cm}=\sqrt{2^2+1}-\sqrt{(-1)^2+1}\\\hspace{1.9cm}=\sqrt{4+1}-\sqrt{1+1}\\\hspace{1.9cm}=\sqrt{5}-\sqrt{2}

Comme \sqrt{5}-\sqrt{2}\approx 0.82, la conjecture précédente faite avec Géogébra permet de valider la réponse.

 

 

Soit I=\int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx et J=\int_{0}^1 \frac{1}{e^x+1}\hspace{0.05cm}dx\\I+J=\int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx+\int_{0}^1 \frac{1}{e^x+1}\hspace{0.05cm}dx

D’après la propriété n°4

\hspace{1cm}=\int_{0}^1 \frac{e^x}{e^x+1}+ \frac{1}{e^x+1}\hspace{0.05cm}dx\\\hspace{1cm}=\int_{0}^1 \frac{e^x+1}{e^x+1}\hspace{0.05cm}dx\\\hspace{1cm}=\int_{0}^1 1\hspace{0.05cm}dx

Une primitive de 1 est x

\hspace{1cm}=[x]_{0}^1 \\\hspace{1cm}=1-0\\\hspace{1cm}=1

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx.

Ensuite on va calculer \int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to \frac{e^x}{e^x+1}.

On cherche de quelle forme est la fonction f(x)=\frac{e^x}{e^x+1} pour pouvoir déterminer une primitive à l’aide du tableau ci-dessous.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

f(x)=\frac{e^x}{e^x+1}  est de la forme \frac{u'(x)}{u(x)} avec u(x)= e^x+1.

1.Je calcule u'(x)

u'(x)= (e^x+1)’

u'(x)= (e^x)’+(1)’

u'(x)= e^x+0

u'(x)= e^x

2.Je remplace u(x) par e^x+1 et u'(x) par e^x dans la formule ci-dessous :

\frac{u'(x)}{u(x)} a pour primitive ln(|u(x)|).

\frac{e^x}{e^x+1} a pour primitive ln(|e^x+1|)

e^x+1 est toujours positif donc |e^x+1|=e^x+1

Donc F(x)=ln(e^x+1)

2.Calcul de l’intégrale.

\int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx=[F(x)]_{0}^{1}\\\hspace{1.6cm}=F(1)-F(0)\\\hspace{1.6cm}=ln(e^1+1)-ln(e^0+1)\\\hspace{1.6cm}=ln(e+1)-ln(1+1)\\\hspace{1.6cm}=ln(e+1)-ln(2)\\\hspace{1.6cm}=ln(\frac{e+1}{2})

Comme ln(\frac{e+1}{2})\approx 0.62, la conjecture précédente faite avec Géogébra permet de valider la réponse.

 

On a montré dans la question 1 que : I+J=1

On a montré dans la question 2 que : I=ln(\frac{e^2+1}{2})

On remplace I par ln(\frac{e^2+1}{2}) dans I+J=1

ln(\frac{e^2+1}{2}) +J=1\\J=1-ln(\frac{e^2+1}{2})

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{-2}^4 |x|\hspace{0.05cm}dx.

Ensuite on va calculer \int_{-2}^4 |x|\hspace{0.05cm}dx à l’aide de la relation de Chasles.

\int_{-2}^4 |x|\hspace{0.05cm}dx=\int_{-2}^0|x|\hspace{0.05cm}dx+\int_{0}^4|x|\hspace{0.05cm}dx

D’après la définition de la valeur absolue.

\hspace{1.5cm}=\int_{-2}^0(-x)\hspace{0.05cm}dx+\int_{0}^4x\hspace{0.05cm}dx

Une primitive de -x est – \frac{x^2}{2} et une primitive de x est \frac{x^2}{2}.

\hspace{1.5cm}=[-\frac{x^2}{2}]_{-2}^0+[\frac{x^2}{2}]_{0}^4

\hspace{1.5cm}=(-\frac{0^2}{2}-(-\frac{(-2)^2}{2}))+(\frac{4^2}{2}-\frac{0^2}{2})

\hspace{1.5cm}=(-\frac{0}{2}-(-\frac{4}{2}))+(\frac{16}{2}-\frac{0}{2})

\hspace{1.5cm}=(0-(-2))+(8-0)

\hspace{1.5cm}=2+8

\hspace{1.5cm}=10

 

 

Pour tout x de [1;e], on a 

1\leq x \leq e

Comme la fonction ln est croissante sur [1;e], les nombres et les images varient dans le même sens.

ln(1)\leq ln(x) \leq ln(e)

On remplace ln(1) par 0 et ln(e) par 1.

0\leq ln(x) \leq 1

 

 

On veut montrer que  0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq \frac{e^3-1}{3}

On a montré que  0\leq ln(x)\leq 1

On multiplie par x^2 les trois membres de l’inégalité. Elle ne change pas de sens car x^2 est positif.

x^2\times 0\leq x^2\times ln(x)\leq x^2\times 1\\0\leq x^2 ln(x)\leq x^2

On utilise : si pour tout x de [a;b], f(x)\geq g(x) alors \int_{a}^b f(x)\hspace{0.05cm}dx\geq \int_{a}^b g(x)\hspace{0.05cm}dx

\int_{1}^e 0\hspace{0.05cm}dx\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq \int_{1}^e x^2\hspace{0.05cm}dx

0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq[\frac{x^3}{3}]_{1}^e

0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq\frac{e^3}{3}-\frac{1^3}{3}

0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq\frac{e^3}{3}-\frac{1}{3}

0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq\frac{e^3-1}{3}

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{1}^e xln(x)\hspace{0.05cm}dx.

On veut calculer \int_{1}^e xln(x)\hspace{0.05cm}dx à l’aide d’une intégration par parties.

On va utiliser \int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

xln(x) est le produit de x par ln(x). On a deux possibilités, on les examine et on garde la bonne.

1.soit on pose 

 u(x)=x 

v'(x) = ln(x). 

On trouve facilement

 u'(x)=1

mais il n’est pas possible de trouver facilement v(x) qui est une primitive de ln(x)

2.soit on pose 

 u(x)=ln(x)

v'(x) = x. 

On trouve facilement

 u'(x)=\frac{1}{x} 

  v(x)=\frac{x^2}{2} 

On pose 

u(x)=ln(x)\\ v'(x) = x.

Donc 

u'(x)=\frac{1}{x}\\ v(x)=\frac{x^2}{2}. 

On remplace u(x) par ln(x), v'(x) par  x, v(x) par \frac{x^2}{2} et u'(x) par \frac{1}{x} dans

\int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

\int_{1}^e xln(x)\hspace{0.05cm}dx=[ln(x)\frac{x^2}{2}]_{1}^e-\int_{1}^e \frac{1}{x}\times \frac{x^2}{2} \hspace{0.05cm}dx

On effectue le produit \frac{1}{x}\times \frac{x^2}{2}=\frac{x}{2}

\hspace{1.95cm}=[ln(x)\frac{x^2}{2}]_{1}^e-\int_{1}^e \frac{x}{2}\hspace{0.05cm}dx

Une primitive de \frac{x}{2} est \frac{x^2}{4}

\hspace{1.95cm}=[ln(x)\frac{x^2}{2}]_{1}^e-[\frac{x^2}{4}]_{1}^e \hspace{0.05cm}dx

Il ne reste plus qu’à appliquer [F(x)]_{a}^b=F(b)-F(a)

\hspace{1.95cm}=(ln(e)\frac{e^2}{2}-ln(1)\frac{1^2}{2})-(\frac{e^2}{4}-\frac{1^2}{4})

\hspace{1.95cm}=(1\times \frac{e^2}{2}-0\times\frac{1^2}{2})-(\frac{e^2}{4}-\frac{1}{4})

\hspace{1.95cm}=\frac{e^2}{2}-\frac{e^2}{4}+\frac{1}{4}

On met au même dénominateur

\hspace{1.95cm}=\frac{e^2}{2}\times \frac{2}{2}-\frac{e^2}{4}+\frac{1}{4} 

\hspace{1.95cm}=\frac{2e^2}{4}-\frac{e^2}{4}+\frac{1}{4} 

\hspace{1.95cm}=\frac{e^2}{4}+\frac{1}{4}(\approx2.1) 

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^1 xe^x\hspace{0.05cm}dx.

On veut calculer \int_{0}^1 xe^x\hspace{0.05cm}dx à l’aide d’une intégration par parties.

On va utiliser \int_{0}^1 u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{0}^1-\int_{0}^1 u'(x)v(x)\hspace{0.05cm}dx

xe^x est le produit de x par e^x. On a deux possibilités, on les examine et on garde la bonne.

1.soit on pose 

 u(x)=x 

v'(x) = e^x. 

On trouve facilement

u'(x)=1

v(x)=e^x 

On trouve facilement la primitive de

u'(x)v(x)=1\times e^x 

2.soit on pose 

 u(x)=e^x

v'(x) = x. 

On trouve facilement

 u'(x)=e^x 

  v(x)=\frac{x^2}{2} 

On complique la situation et on doit ensuite trouver une primitive de

  u'(x)v(x)=e^x\times \frac{x^2}{2} 

On pose 

u(x)=x\\ v'(x) = e^x.

Donc 

u'(x)=1\\ v(x)=e^x. 

On remplace u(x) par x, v'(x) par  e^x, u'(x) par 1 et  v(x) par e^x dans

\int_{0}^1 u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{0}^1-\int_{0}^1 u'(x)v(x)\hspace{0.05cm}dx

\int_{0}^1 xe^x\hspace{0.05cm}dx=[xe^x]_{0}^1-\int_{1}^e 1\times e^x \hspace{0.05cm}dx

\hspace{1.50cm}=[xe^x]_{0}^1-\int_{1}^e e^x \hspace{0.05cm}dx

Une primitive de e^x est e^x

\hspace{1.50cm}=[xe^x]_{0}^1-[e^x]_{0}^1 \hspace{0.05cm}dx

Il ne reste plus qu’à appliquer [F(x)]_{a}^b=F(b)-F(a)

\hspace{1.50cm}=(1\times e^1-0\times e^0)-(e^1-e^0)

\hspace{1.50cm}=e-(e-1)

\hspace{1.50cm}=e-e+1

\hspace{1.50cm}=1

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^{\frac{\pi} {3}}(x-1)cos(x) \hspace{0.05cm}dx.

On veut calculer \int_{0}^{\frac{\pi} {3}}(x-1)cos(x) \hspace{0.05cm}dx à l’aide d’une intégration par parties.

On va utiliser \int_{0}^{\frac{\pi} {3}} u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{0}^{\frac{\pi} {3}}-\int_{0}^{\frac{\pi} {3}} u'(x)v(x)\hspace{0.05cm}dx

(x-1)cos(x) est le produit de (x-1) par cos(x). On a deux possibilités, on les examine et on garde la bonne.

1.soit on pose 

 u(x)=x-1 

v'(x) = cos(x). 

On trouve facilement

u'(x)=1

v(x)=sin(x) 

On trouve facilement la primitive de

u'(x)v(x)=1\times sin(x) 

2.soit on pose 

 u(x)=cos(x)

v'(x) = (x-1). 

On trouve facilement

 u'(x)=-sin(x) 

  v(x)=\frac{x^2}{2}-x 

On complique la situation et on doit ensuite trouver une primitive de

  u'(x)v(x)=-sin(x)\times ( \frac{x^2}{2}-x) 

On pose 

u(x)=x-1\\ v'(x) = cos(x).

Donc 

u'(x)=1\\ v(x)=sin(x). 

On remplace u(x) par x-1, v'(x) par  cos(x), u'(x) par 1 et  v(x) par sin(x) dans

\int_{0}^{\frac{\pi} {3}} u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{0}^{\frac{\pi} {3}}-\int_{0}^{\frac{\pi} {3}} u'(x)v(x)\hspace{0.05cm}dx

\int_{0}^{\frac{\pi} {3}}(x-1)cos(x) \hspace{0.05cm}dx=[(x-1)sin(x)]_{0}^{\frac{\pi} {3}}-\int_{0}^{\frac{\pi} {3}} 1\times sin(x) \hspace{0.05cm}dx

\hspace{3cm}=[(x-1)sin(x)]_{0}^{\frac{\pi} {3}}-\int_{0}^{\frac{\pi} {3}} sin(x) \hspace{0.05cm}dx \hspace{0.05cm}dx

Une primitive de sin(x) est -cos(x)

\hspace{3cm}=[(x-1)sin(x)]_{0}^{\frac{\pi} {3}}-[-cos(x)]_{0}^{\frac{\pi} {3}}

Il ne reste plus qu’à appliquer [F(x)]_{a}^b=F(b)-F(a)

\hspace{3cm}=((\frac{\pi} {3}-1)sin(\frac{\pi} {3})-(0-1)sin(0))-(-cos(\frac{\pi} {3})-(-cos(0))

\hspace{3cm}=((\frac{\pi} {3}-1)\times\frac{\sqrt{3}} {2})-(-1)\times 0)-(-\frac{1} {2}+1)

\hspace{3cm}=(\frac{\pi} {3}-1)\times\frac{\sqrt{3}} {2})-(-\frac{1} {2}+\frac{2} {2})

\hspace{3cm}=(\frac{\pi} {3}-1)\times\frac{\sqrt{3}} {2}-\frac{1} {2}(\approx{-0.46})

 

 

On peut utiliser Géogébra pour conjecturer la valeur de \int_{1}^e ln(x)\hspace{0.05cm}dx.

On veut calculer \int_{1}^e ln(x)\hspace{0.05cm}dx à l’aide d’une intégration par parties.

On va utiliser \int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

ln(x) est le produit de 1 par ln(x). On a deux possibilités, on les examine et on garde la bonne.

1.soit on pose 

 u(x)=1 

v'(x) = ln(x). 

On trouve facilement

 u'(x)=0

mais il n’est pas possible de trouver facilement v(x) qui est une primitive de ln(x)

2.soit on pose 

 u(x)=ln(x)

v'(x) = 1. 

On trouve facilement

 u'(x)=\frac{1}{x} 

  v(x)=x 

On pose 

u(x)=ln(x)\\ v'(x) = 1.

Donc 

u'(x)=\frac{1}{x}\\ v(x)=x. 

On remplace u(x) par ln(x), v'(x) par  1, v(x) par x et u'(x) par \frac{1}{x} dans

\int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

\int_{1}^e ln(x)\hspace{0.05cm}dx=[ln(x)x]_{1}^e-\int_{1}^e \frac{1}{x}\times x \hspace{0.05cm}dx

On effectue le produit \frac{1}{x}\times {x}=1

\hspace{1.75cm}=[ln(x)x]_{1}^e-\int_{1}^e 1\hspace{0.05cm}dx

Une primitive de 1 est x

\hspace{1.75cm}=[ln(x)\frac{x^2}{2}]_{1}^e-[x]_{1}^e \hspace{0.05cm}dx

Il ne reste plus qu’à appliquer [F(x)]_{a}^b=F(b)-F(a)

\hspace{1.75cm}=(ln(e)\times e-ln(1)\times 1)-(e-1)

\hspace{1.75cm}=(1\times e-0\times 1)-(e-1)

\hspace{1.75cm}=e-e+1

\hspace{1.75cm}=1

 

 

 

 f(x)=\frac{ln(x)}{x^2}.

Sur l’intervalle [1;e], ln(x) est positif, de plus x^2 est positif donc f(x) est positif et l’aire ( en unités d’aire) de la partie du plan limitée par x=1 , x=e , C_f et l’axe des abscisses est égale à :

  \int_{1}^e f(x)\hspace{0.05cm}dx

On peut utiliser Géogébra pour conjecturer la valeur de \int_{1}^e f(x)\hspace{0.05cm}dx.

Ensuite on va calculer \int_{1}^e f(x)\hspace{0.05cm}dx=\int_{1}^e \frac{ln(x)}{x^2}\hspace{0.05cm}dx   à l’aide d’une intégration par parties.

On va utiliser \int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

\frac{ln(x)}{x^2} est, par exemple,  le produit de \frac{1}{x^2} par ln(x). On a deux possibilités, on les examine et on garde la bonne.

1.soit on pose 

 u(x)=\frac{1}{x^2} 

v'(x) = ln(x). 

On trouve 

 u'(x)=-\frac{2x}{(x^2)^2}

mais il n’est pas possible de trouver facilement v(x) qui est une primitive de ln(x)

2.soit on pose 

 u(x)=ln(x)

v'(x) = \frac{1}{x^2}. 

On trouve facilement

 u'(x)=\frac{1}{x} 

  v(x)=-\frac{1}{x} 

On pose 

u(x)=ln(x)\\ v'(x) = \frac{1}{x^2}.

Donc 

u'(x)=\frac{1}{x}\\ v(x)=-\frac{1}{x}. 

On remplace u(x) par ln(x), v'(x) par  \frac{1}{x^2}, v(x) par -\frac{1}{x} et u'(x) par \frac{1}{x} dans

\int_{1}^e u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{1}^e-\int_{1}^e u'(x)v(x)\hspace{0.05cm}dx

\int_{1}^e \frac{ln(x)}{x^2}\hspace{0.05cm}dx=[ln(x)\times(-\frac{1}{x})]_{1}^e-\int_{1}^e \frac{1}{x}\times (-\frac{1}{x}) \hspace{0.05cm}dx

On effectue le produit \frac{1}{x}\times (-\frac{1}{x})=-\frac{1}{x^2}

\hspace{1.6cm}=[-\frac{ln(x)}{x}]_{1}^e-\int_{1}^e (-\frac{1}{x^2}) \hspace{0.05cm}dx

Une primitive de -\frac{1}{x^2} est \frac{1}{x}

\hspace{1.6cm}=[-\frac{ln(x)}{x}]_{1}^e-[\frac{1}{x}]_{1}^e \hspace{0.05cm}dx

Il ne reste plus qu’à appliquer [F(x)]_{a}^b=F(b)-F(a)

\hspace{1.6cm}=(-\frac{ln(e)}{e}-(-\frac{ln(1)}{1}))-(\frac{1}{e}-\frac{1}{1})

\hspace{1.6cm}=(-\frac{1}{e}-(-\frac{0}{1}))-(\frac{1}{e}-1)

\hspace{1.6cm}=-\frac{1}{e}-\frac{1}{e}+1

\hspace{1.6cm}=-\frac{2}{e}+1(\approx0.26)

 

 

f(x)=-2xe^{-x^2}.

Sur l’intervalle [0;3] , -2x est négatif et e^{-x^2} est positif donc  f(x) est négatif .

L’aire ( en unités d’aire) de la partie du plan limitée par x=0 , x=3 , C_f et l’axe des abscisses est égale à :

  -\int_{0}^3 f(x)\hspace{0.05cm}dx

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^3 f(x)\hspace{0.05cm}dx.

\int_{0}^3 f(x)\hspace{0.05cm}dx=-1 l’aire mesure -(-1)=1

Ensuite on va calculer -\int_{0}^3 f(x)\hspace{0.05cm}dx=-\int_{0}^3 -2xe^{-x^2}\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction x\to -2xe^{-x^2}.

A l’aide du tableau ci-dessous on cherche une primitive de -2xe^{-x^2}.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

-2xe^{-x^2} est de la forme u'(x)e^{u(x)} avec u(x)= -x^2.

1.Je calcule u'(x)

u'(x)= (-x^2)’

u'(x)=-2x

2.Je remplace u(x) par -x^2 et u'(x) par -2x dans la formule ci-dessous :

u'(x)e^{u(x)} a pour primitive e^{u(x)}.

-2xe^{-x^2} a pour primitive e^{-x^2}

2.Calcul de l’intégrale.

\int_{0}^3-2xe^{-x^2}\hspace{0.05cm}dx=[F(x)]_{0}^3\\\hspace{2.25cm}=F(3)-F(0)\\\hspace{2.25cm}=(e^{-3^2})-(e^{-0^2})\\\hspace{2.25cm}=(e^{-9})-(e^{0})\\\hspace{2.25cm}=\frac{1}{e^9}-1

Donc l’aire mesure

-(\frac{1}{e^9}-1)=-\frac{1}{e^9}+1\approx 1

 

 

Comme f(x)\geq g(x) l’aire ( en unités d’aire) de la partie du plan limitée par x=0 , x=1 , C_f et C_g est égale à :

  \int_{0}^1 (f(x)-g(x))\hspace{0.05cm}dx

On peut utiliser Géogébra pour conjecturer la valeur de \int_{0}^1 (f(x)-g(x))\hspace{0.05cm}dx.

Ensuite on va calculer \int_{0}^1 (f(x)-g(x))\hspace{0.05cm}dx=\int_{0}^1 e^x-2e^{\frac{x}{2}}+1\hspace{0.05cm}dx.

1.Calcul d’une primitive de la fonction e^x-2e^{\frac{x}{2}}+1.

La fonction est la somme de trois termes e^x , 2e^{\frac{x}{2}} et 1.

a. A l’aide du tableau ci-dessous on cherche des primitives de e^x et 1.

La fonction f(x)a pour primitive F(x)sur l’intervalle
f(x)=kF(x)=kx\mathbf{R}
f(x)=xF(x)=\frac{x^2}{2}\mathbf{R}
f(x)=x^2F(x)=\frac{x^3}{3}\mathbf{R}
f(x)=x^n

( si n\in \mathbf{Z}, n\ne 0, n\ne -1)

F(x)=\frac{x^{n+1}}{n+1}

\mathbf{R} si n>0

]-\infty;0[\cup]0;+\infty[ si n<-1

f(x)=-\frac{1}{x^2}F(x)=\frac{1}{x}]-\infty;0[\cup]0;+\infty[
f(x)=\frac{1}{x}F(x)=ln(x)]0;+\infty[
f(x)=\frac{1}{\sqrt{x}}F(x)=2\sqrt{x}]0;+\infty[
f(x)=sin(x)F(x)=-cos(x)\mathbf{R}
f(x)=cos(x)F(x)=sin(x)\mathbf{R}
f(x)=e^xF(x)=e^x\mathbf{R}

Une primitive de e^x est e^x.

Une primitive de 1 est x.

b. A l’aide du tableau ci-dessous on cherche une primitive de 2e^{\frac{x}{2}}.

La fonction f(x) est de la formeelle a pour primitive  F(x) Conditions
f(x)=u'(x)\times u^n(x)F(x)=\frac{u^{n+1}(x)}{n+1}si n>-1, u(x)\ne 0
f(x)=\frac{u'(x)}{u^2(x)}F(x)=-\frac{1}{u(x)}u(x)\ne  0
f(x)=\frac{u'(x)}{u(x)}F(x)=ln(|u(x)|)u(x)\ne 0
f(x)=\frac{u'(x)}{2\sqrt{u(x)}}F(x)=\sqrt{u(x)}u(x)> 0
f(x)=u'(x)\times e^{u(x)}F(x)=e^{u(x)} 
(v’ou)\times u’vouv est une fonction dérivable sur J et u(x)\in J

2e^{\frac{x}{2}} est de la forme u'(x)e^{u(x)} avec u(x)= \frac{x}{2}.

1.Je calcule u'(x)

u'(x)= (\frac{x}{2})’

u'(x)=\frac{1}{2}(x)’

u'(x)=\frac{1}{2}\times 1

u'(x)=\frac{1}{2}

2.Je remplace u(x) par \frac{x}{2} et u'(x) par \frac{1}{2} dans la formule ci-dessous :

u'(x)e^{u(x)} a pour primitive e^{u(x)}.

\frac{1}{2}e^{\frac{x}{2}} a pour primitive e^{\frac{x}{2}}

Pour retrouver 2e^{\frac{x}{2}} à gauche, il faut multiplier par 4.

2e^{\frac{x}{2}}a pour primitive 4e^{\frac{x}{2}}

c. Une primitive d’une somme est la somme des primitives, donc :

Une primitive de e^x-2e^{\frac{x}{2}}+1 est e^x-4e^{\frac{x}{2}}+x

2.Calcul de l’intégrale.

\int_{0}^1(e^x-4e^{\frac{x}{2}}+x)\hspace{0.05cm}dx=[F(x)]_{0}^1\\\hspace{3.1cm}=F(1)-F(0)\\\hspace{3.1cm}=(e^1-4e^{\frac{1}{2}}+1)-(e^0-4e^{\frac{0}{2}}+0)\\\hspace{3.1cm}=(e-4\sqrt{e}+1)-(1-4e^0)\\\hspace{3.1cm}=(e-4\sqrt{e}+1)-(1-4)\\\hspace{3.1cm}=(e-4\sqrt{e}+1)-(-3)\\\hspace{3.1cm}=e-4\sqrt{e}+1+3\\\hspace{3.1cm}=e-4\sqrt{e}+4(\approx{0.12})

 

 

La valeur moyenne de f sur [a;b] est égale à

  \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx.

On remplace f(x) par x^2, a par 0 et b par 4 dans \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx

\frac{1}{4-0}\int_{0}^4 x^2\hspace{0.05cm}dx=\frac{1}{4}\int_{0}^4 x^2\hspace{0.05cm}dx

On conjecture avec Géogébra :

Donc la valeur moyenne de f sur [0;4] vaut \frac{1}{4}\times 21.33=5.33

Maintenant on calcule   

\frac{1}{4-0}\int_{0}^4 x^2\hspace{0.05cm}dx=\frac{1}{4}\int_{0}^4 x^2\hspace{0.05cm}dx

Une primitive de x^2 est \frac{x^3}{3}.

\hspace{1.9cm}=\frac{1}{4}[\frac{x^3}{3}]_{0}^4

\hspace{1.9cm}=\frac{1}{4}(\frac{4^3}{3}-\frac{0^3}{3})

\hspace{1.9cm}=\frac{1}{4}(\frac{64}{3}-\frac{0}{3})

\hspace{1.9cm}=\frac{1}{4}\times \frac{64}{3}

\hspace{1.9cm}=\frac{8}{3}

La valeur moyenne de f sur [0;4] est égale à \frac{16}{3} .

 

 

La valeur moyenne de f sur [a;b] est égale à

  \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx.

On remplace f(x) par \frac{1}{x}, a par 1 et b par e dans \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx

\frac{1}{e-1}\int_{1}^e \frac{1}{x}\hspace{0.05cm}dx

On conjecture avec Géogébra :

Donc la valeur moyenne de f sur [1;e] vaut \frac{1}{e-1}

Maintenant on calcule   

\frac{1}{e-1}\int_{1}^e \frac{1}{x}\hspace{0.05cm}dx

Une primitive de \frac{1}{x} est ln(x).

\frac{1}{e-1}\int_{1}^e \frac{1}{x}\hspace{0.05cm}dx=\frac{1}{e-1}[ln(x)]_1^{e}

\hspace{1.8cm}=\frac{1}{e-1}(ln(e)-ln(1))

\hspace{1.8cm}=\frac{1}{e-1}(1-0)

\hspace{1.8cm}=\frac{1}{e-1}

La valeur moyenne de f sur [1;e] est égale à \frac{1}{e-1} .

 

La valeur moyenne de f sur [a;b] est égale à

  \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx.

On remplace f(x) par e^x, a par 0 et b par 1 dans \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx

\frac{1}{1-0}\int_{0}^1 e^x\hspace{0.05cm}dx=\int_{0}^1 e^x\hspace{0.05cm}dx

On conjecture avec Géogébra :

Donc la valeur moyenne de f sur [0;1] vaut 1.72

Maintenant on calcule   

\frac{1}{1-0}\int_{0}^1 e^x\hspace{0.05cm}dx=\int_{0}^1 e^x\hspace{0.05cm}dx

Une primitive de e^x est e^x.

\hspace{1.9cm}=[e^x]_{0}^1

\hspace{1.9cm}=e^1-e^0

\hspace{1.9cm}=e-1\approx 1.72

La valeur moyenne de f sur [0;1] est égale à e-1.

 

 

La valeur moyenne de f sur [a;b] est égale à

  \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx.

On remplace f(x) par -sin(x), a par -\pi et b par \pi dans \frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx

\frac{1}{\pi-(-\pi)}\int_{-\pi}^\pi (-sin(x))\hspace{0.05cm}dx=\frac{1}{2\pi}\int_{-\pi}^\pi (-sin(x))\hspace{0.05cm}dx

On conjecture avec Géogébra :

Donc la valeur moyenne de f sur [-\pi;\pi] vaut 0

Maintenant on calcule   

\frac{1}{\pi-(-\pi)}\int_{-\pi}^\pi (-sin(x))\hspace{0.05cm}dx=\frac{1}{2\pi}\int_{-\pi}^\pi (-sin(x))\hspace{0.05cm}dx

Une primitive de -sin(x) est cos(x).

\hspace{3.7cm}=[cos(x)]_{0}^1

\hspace{3.7cm}=cos(\pi)-cos(-\pi)

\hspace{3.7cm}=-1-(-1)

\hspace{3.7cm}=0

La valeur moyenne de f sur [-\pi;\pi] est égale à 0.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.