logo

2. Factoriser en seconde : exercices.

Sommaire

Exercice n°1 

Factoriser en utilisant un facteur commun.

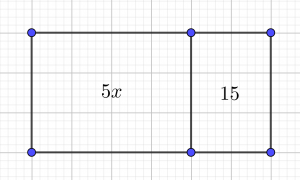
1) 5x+15

illustration géométrique
méthode
correction

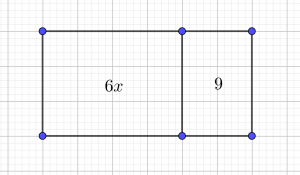
2) 6x+9

illustration géométrique
méthode
correction

3) 4x-8x^{2}

méthode
correction

4) 3x^{2}+6x+9

méthode
correction

5) 5x^{3}+10x^{2}+35x

méthode
correction

6) 2x(x+2)+3(x+2)

méthode
correction

7) 2x(3x-2)+4(3x-2)

méthode
correction

Pour valider les réponses aux questions, utiliser la page Géogébra ci-dessous. Pour ce faire saisir par exemple sur la

ligne 1 : 5x+15 puis cliquer sur le quatrième  onglet en haut à partir de la gauche, sur la ligne suivante s’affiche Factoriser 5(x+3).

Exercice n°2 

Factoriser en utilisant l’identité remarquable a^{2}+2ab+b^{2}=(a+b)^{2} .

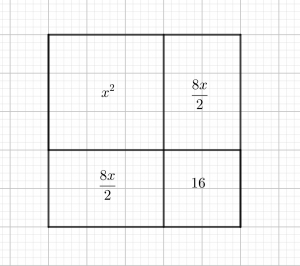
1) x^{2}+8x+16

illustration géométrique
méthode
correction

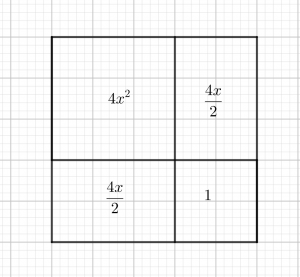
2) 4x^{2}+4x+1

illustration géométrique
méthode
correction

3) x^{2}+x+\frac{1}{4}

méthode
correction

4) \frac{x^{2}}{9}+4x+36

méthode
correction

5) x^{2}+2\sqrt{2}x+2

méthode
correction

6) 3x^{2}+6\sqrt{2}x+6

méthode
correction

Pour valider les réponses aux questions, utiliser la page Géogébra ci-dessous. Pour ce faire saisir par exemple sur la

ligne 1 : x^2+8x+16 puis cliquer sur le quatrième  onglet en haut à partir de la gauche, sur la ligne suivante s’affiche Factoriser (x+4)^2.

Pour saisir racine carrée de 2 taper sqrt(2).

Exercice n°3

Factoriser en utilisant l’identité remarquable a^{2}-2ab+b^{2}=(a-b)^{2} .

1) x^{2}-20x+100

méthode
correction

2) 9x^{2}-12x+4

méthode
correction

3) 144x^{2}-24x+1

méthode
correction

4) \frac{x^{2}}{25}-\frac{4}{5}x+4

méthode
correction

5) x^{2}-\frac{4}{3}x+\frac{4}{9}

méthode
correction

6) \frac{x^{2}}{25}-\frac{3}{5}x+\frac{9}{4}

méthode
correction

7) x^{2}-2\sqrt{5}x+5

méthode
correction

8) 3x^{2}-2\sqrt{21}x+7

méthode
correction

Pour valider les réponses aux questions, utiliser la page Géogébra ci-dessous. Pour ce faire saisir par exemple sur la

ligne 1 : x^2-20x+100 puis cliquer sur le quatrième  onglet en haut à partir de la gauche, sur la ligne suivante s’affiche Factoriser (x-10)^2.

Pour saisir racine carrée de 5 taper sqrt(5).

Exercice n°4

Factoriser en utilisant l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) .

1) x^{2}-64

méthode
correction

2) 81x^{2}-4

méthode
correction

3) 49x^{2}-169

méthode
correction

4) x^{2}-2

méthode
correction

5) 3x^{2}-5

méthode
correction

6) \frac{4x^{2}}{9}-1

méthode
correction

7) \frac{9x^{2}}{16}-5

méthode
correction

8) (2x-1)^{2}-(x+4)^{2}

méthode
correction

Pour valider les réponses aux questions, utiliser la page Géogébra ci-dessous. Pour ce faire saisir par exemple sur la

ligne 1 : x^2-64 puis cliquer sur le quatrième  onglet en haut à partir de la gauche, sur la ligne suivante s’affiche Factoriser (x-8)(x+8).

Pour saisir racine carrée de 5 taper sqrt(5).

Exercice n°5

Factoriser en utilisant la ou les méthode(s)  adéquate(s). En effet après avoir mis en facteur un éventuel facteur commun, il se peut que l’on puisse utiliser une identité remarquable pour factoriser le second facteur.

1) 2x^{2}-4x

correction

2) 8x^{2}-32

correction

3) 2x^{2}-18

correction

4) 2x^{2}+4x+2

correction

5) 2x^{2}+4x+2

correction

6) 2(x-1)^{2}-8

correction

7) 3(2x+1)^{2}+27

correction

8) 5(3x+1)^{2}-45

correction

Pour valider les réponses aux questions, utiliser la page Géogébra ci-dessous. Pour ce faire saisir par exemple sur la

ligne 1 : 2x^2-4x puis cliquer sur le quatrième  onglet en haut à partir de la gauche, sur la ligne suivante s’affiche Factoriser 2x(x-2).

©2020 – Math’O karé SAS

Il s’agit d’illustrer géométriquement la factorisation de 5x+15.

5x et 15 sont les aires des deux rectangles qui apparaissent dans la figure ci-dessous. Ces deux rectangles ont la même largeur, ici 5 . Ils auront donc pour longueurs respectives x et 3.

Les dimensions du rectangle obtenu en réunissant les deux aires sont 5 et (x+3) . Son aire sera donc égale à 5(x+3) .

Ainsi 5x+15=5(x+3)

 Méthode: Si vous avez trouvé un facteur commun aux deux termes d’une somme, écrire les deux termes sous la forme de deux produits de deux facteurs dont l’un est commun aux deux. Utiliser le diagramme suivant.

Premier terme        =   facteur commun   \times  deuxième facteur n°1

Deuxième terme    =   facteur commun     \times deuxième facteur n°2

Puis écrire la somme sous la forme

facteur commun    ( deuxième facteur n°1  + ( ou –) deuxième facteur n°2)

Factorisons 5x+15

5x={5}\times{x}

15={5}\times{3}

5x+15=5(x+3)

Il s’agit d’illustrer géométriquement la factorisation de 6x+9.

6x et 9 sont les aires des deux rectangles qui apparaissent dans la figure ci-dessous. Ces deux rectangles ont la même largeur, ici 3 . Ils auront donc pour longueurs respectives 2x et3.

Les dimensions du rectangle obtenu en réunissant les deux aires sont 3 et (2x+3) . Son aire sera donc égale à 3(2x+3) .

Ainsi 6x+9=3(2x+3)

Factorisons 6x+9

6x={3}\times{2x}

9={3}\times{3}

6x+9=3(2x+3)

Factorisons 4x-8x^{2}

4x={4x}\times{1}

8x^{2}={4x}\times{2x}

4x-8x^{2}=4x(1-2x)

Les factorisations suivantes sont correctes mais en règle générale on choisit  la factorisation qui utilise le plus grand facteur commun possible.

4x-8x^{2}=2(2x-4x^{2})

4x-8x^{2}=4(x-2x^{2})

4x-8x^{2}=x(4-8x)

4x-8x^{2}=2x(2-4x)

 Méthode: Si vous avez trouvé un facteur commun aux trois termes d’une somme, écrire les trois  termes sous la forme de trois produits de deux facteurs dont l’un est commun aux trois. Utiliser le diagramme suivant.

Premier terme        =   facteur commun   \times  deuxième facteur n°1

Deuxième terme    =   facteur commun     \timesdeuxième facteur n°2

Troisième terme    =   facteur commun     \timesdeuxième facteur n°3

 Puis écrire la somme sous la forme

facteur commun    ( deuxième facteur n°1  + ( ou –) deuxième facteur n°2+ ( ou –) deuxième facteur n°3)

Factorisons 3x^{2}+6x+9

3x^{2}={3}\times{x^{2}}

6x={3}\times{2x}

9={3}\times{3}

3x^{2}+6x+9=3(x^{2}+2x+3)

Factorisons 5x^{3}+10x^{2}+35x

5x^{3}={5x}\times{x^{2}}

10x^{2}={5x}\times{2x}

35x={5x}\times{7}

5x^{3}+10x^{2}+35x=5x(x^{2}+2x+7)

Factorisons 2x(x+2)+3(x+2)

2x(x+2)={(x+2)}\times{2x}

3(x+2)={(x+2)}\times{3}

2x(x+2)+3(x+2)=(x+2)(2x+3)

Factorisons 2x(3x-2)+4(3x-2)

2x(3x-2)={(3x-2)}\times{2x}

4(3x-2)={(3x-2)}\times{4}

2x(3x-2)+4(3x-2)=(3x-2)(2x+4)

Il s’agit d’illustrer la factorisation de x^{2}+8x+16.

Sur la figure ci-dessous, les deux carrés ont pour aires respectives x^{2} et 16.

Leurs côtés respectifs mesurent donc x et 4.

On vérifie que l’aire de chaque rectangle mesure la moitié de 8x . Ce qui est le cas car ses dimensions sont x et 4.

Le grand carré a donc pour aire (x+4)^{2} puisque son côté mesure (x+4) .

Ainsi 

x^{2}+8x+16=(x+4)^{2}  

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

a^{2}=x^{2} donc a=x

b^{2}=16  donc b=4

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{4}=8x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+8x +16= (x+4)^{2}

Il s’agit d’illustrer la factorisation de 4x^{2}+4x+1.

Sur la figure ci-dessous, les deux carrés ont pour aires respectives 4x^{2} et 1.

Leurs côtés respectifs mesurent donc 2x et 1.

On vérifie que l’aire de chaque rectangle mesure la moitié de 4x . Ce qui est le cas car ses dimensions sont 2x et 1.

Le grand carré a donc pour aire (2x+1)^{2} puisque son côté mesure (2x+1) .

Ainsi 

4x^{2}+4x+1=(2x+1)^{2}  

a^{2}=4x^{2} donc a=2x

b^{2}=1  donc b=1

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{2x}\times{1}=4x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

4x^{2}+4x +1= (2x+1)^{2}

a^{2}=x^{2} donc a=x

b^{2}=\frac{1}{4}  donc b=\frac{1}{2}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{\frac{1}{2} }=x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+x +\frac{1}{4} = (x+\frac{1}{2} )^{2}

a^{2}=\frac{x^{2}}{9} donc a=\frac{x}{3}

b^{2}=36  donc b=6

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{3}}\times{6}=4x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

\frac{x^{2}}{9}+4x +36= (\frac{x}{3}+6)^{2}

a^{2}=x^{2} donc a=x

b^{2}=2  donc b=\sqrt{2} 

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{\sqrt{2}}=2\sqrt{2}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

x^{2}+2\sqrt{2}x +2= (x+\sqrt{2})^{2}

a^{2}=3x^{2} donc a=\sqrt{3}x

b^{2}=6  donc b=\sqrt{6}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\sqrt{3}x}\times{\sqrt{6}}=2\sqrt{18}x={2}\times{3\sqrt{2}}x=6\sqrt{2}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}+2ab +b^{2}= (a+b)^{2}

3x^{2}+6\sqrt{2}x +6= (\sqrt{3}x+\sqrt{6})^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

a^{2}=x^{2} donc a=x

b^{2}=100  donc b=10

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{10}=20x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

x^{2}-20x +100= (x-10)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=9x^{2} donc a=3x\\b^{2}=4  donc b=2

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{3x}\times{2}=12x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

9x^{2}-12x +4= (3x-2)^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=144x^{2} donc a=12x\\b^{2}=1  donc b=1

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{12x}\times{1}=24x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

144x^{2}-24x +1= (12x-1)^{2}

a^{2}=\frac{x^{2}}{25} donc a=\frac{x}{5}\\b^{2}=4  donc b=2

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{5}}\times{2}=\frac{4}{5}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

\frac{x^{2}}{25}-\frac{4}{5}x +4= (\frac{x}{5}-2)^{2}

a^{2}=x^{2} donc a=x

b^{2}=\frac{4}{9}  donc b=\frac{2}{3}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{\frac{2}{3}}=\frac{4}{3}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

x^{2}-\frac{4}{3}x +\frac{4}{9} = (x-\frac{2}{3})^{2}

a^{2}=\frac{x^{2}}{25} donc a=\frac{x}{5}\\b^{2}=\frac{9}{4} donc b=\frac{3}{2}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\frac{x}{5}}\times{\frac{3}{2}}=\frac{6}{10}x=\frac{3}{5}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

\frac{x^{2}}{25}-\frac{3}{5}x +\frac{9}{4}= (\frac{x}{5}-\frac{3}{2})^{2}

a^{2}=x^{2} donc a=x\\b^{2}=5 donc b=\sqrt{5}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{x}\times{\sqrt{5}}=2\sqrt{5}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

x^{2}-2\sqrt{5}x +5= (x-\sqrt{5})^{2}

a^{2}=3x^{2} donc a=\sqrt{3}x\\b^{2}=7  donc b=\sqrt{7}

Ensuite je calcule le double produit 2ab en remplaçant  a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ. 

{2}\times{a}\times{b}={2}\times{\sqrt{3}x}\times{\sqrt{7}}=2\sqrt{21}x

Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :

a^{2}-2ab +b^{2}= (a-b)^{2}

3x^{2}-2\sqrt{21}x +7= (\sqrt{3}x-\sqrt{7})^{2}

Le plus simple est d’abord de compléter les pointillés ci-dessous:

a^{2}=…  donc a=…\\b^{2}=…  donc b=…

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

a^{2}=x^{2}  donc a=x

b^{2}=64  donc b=8

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

x^{2}-64= (x-8)(x+8)

a^{2}=81x^{2}  donc a=9x

b^{2}=4 donc b=2

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

81x^{2}-4= (9x-2)(9x+2)

a^{2}=49x^{2}  donc a=7x

b^{2}=169  donc b=13

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

49x^{2}-169= (7x-13)(7x+13)

a^{2}=x^{2}  donc a=x

b^{2}=2  donc b=\sqrt{2}

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

x^{2}-2= (x-\sqrt{2})(x+\sqrt{2})

a^{2}=3x^{2}  donc a=\sqrt{3}x

b^{2}=5  donc b=\sqrt{5}

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

3x^{2}-5= (\sqrt{3}x-\sqrt{5})(\sqrt{3}x+\sqrt{5})

a^{2}=\frac{4x^{2}}{9}  donc a=\frac{2x}{3}

b^{2}=1  donc b=1

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

\frac{4x^{2}}{9}-1= (\frac{2x}{3}-1)(\frac{2x}{3}+1)

a^{2}=\frac{9x^{2}}{16}  donc a=\frac{3x}{4} 

b^{2}=5  donc b=\sqrt{5}

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

\frac{9x^{2}}{16}-5= (\frac{3x}{4}  -\sqrt{5})(\frac{3x}{4}  +\sqrt{5})

a^{2}=(2x-1)^{2}  donc a=2x-1

b^{2}=(x+4)^{2}  donc b=x+4

Pour finir, il suffit de remplacer a, b , a^{2},  et b^{2} par leurs valeurs dans :

a^{2}-b^{2}= (a-b)(a+b)

(2x-1)^{2}-(x+4)^{2} = ((2x-1)-(x+4))((2x-1)+(x+4))\\\hspace{3.3cm} = (2x-1-x-4))(2x-1+x+4)\\\hspace{3.3cm} = (x-5)(3x+5)

Factorisons 2x^{2}-4x .

Y’a-t-il un facteur commun ? Oui :2x.

8x^{2}={2x}\times{x}

4x={2x}\times{2}

2x^{2}-4x=2x(x-2)

Factorisons 8x^{2}-32 .

Y’a-t-il un facteur commun ? Oui :8.

8x^{2}={8}\times{x^{2}}

32={8}\times{4}

8x^{2}-32=8(x^{2}-4)

Peut-on factoriser x^{2}-4 à l’aide de l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) puisqu’il n’y a que deux termes ? Oui car x^{2}-4 est la différence de deux carrés.

a^{2}=x^{2} donc a=x

b^{2}=4 donc b=2

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}-b^{2}=(a-b)(a+b) 

x^{2}-4=(x-2)(x+2)

Ainsi    8x^{2}-32=8(x-2)(x+2) 

Factorisons 2x^{2}-18 .

Y’a-t-il un facteur commun ? Oui :2.

2x^{2}={2}\times{x^{2}}

18={2}\times{9}

2x^{2}-18=2(x^{2}-9)

Peut-on factoriser x^{2}-9 à l’aide de l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) puisqu’il n’y a que deux termes ? Oui car x^{2}-9 est la différence de deux carrés.

a^{2}=x^{2} donc a=x

b^{2}=9 donc b=3

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}-b^{2}=(a-b)(a+b) 

x^{2}-9=(x-3)(x+3)

Ainsi    2x^{2}-18=2(x-3)(x+3) 

Factorisons 2x^{2}+4x+2 .

Y’a-t-il un facteur commun ? Oui :2.

2x^{2}={2}\times{x^{2}}

4x={2}\times{2x}

2={2}\times{1}

2x^{2}+4x+2=2(x^{2}+2x+1)

Peut-on factoriser x^{2}+2x+1 à l’aide de l’identité remarquable a^{2}+2ab+b^{2}=(a+b)^{2} puisqu’il y a trois termes et un plus ? Oui car 

x^{2} et 1 sont les carrés de x et 1 et  2x est le double produit de x et 1

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}+2ab+b^{2}=(a+b)^{2} 

x^{2}+2x+1=(x+1)^{2}

Ainsi  2x^{2}+4x+2=2(x+1)^{2}

Factorisons 3x^{2}-12x+12 .

Y’a-t-il un facteur commun ? Oui :3.

3x^{2}={3}\times{x^{2}}

12x={3}\times{4x}

12={3}\times{4}

3x^{2}-12x+12=3(x^{2}-4x+4)

Peut-on factoriser x^{2}-4x+4 à l’aide de l’identité remarquable a^{2}-2ab+b^{2}=(a-b)^{2} puisqu’il y a trois termes et un moins ? Oui car 

x^{2} et 4 sont les carrés de x et 2 et  4x est le double produit de  x et 2.

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}-2ab+b^{2}=(a-b)^{2}

x^{2}-4x+4=(x-2)^{2}

Ainsi  3x^{2}-12x+12=3(x-2)^{2}

Factorisons 2(x-1)^{2}-8 .

Y’a-t-il un facteur commun ? Oui :2.

2(x-1)^{2}={2}\times{(x-1)^{2}}

8={2}\times{4}

2(x-1)^{2}-8=2((x-1)^{2}-4)

Peut-on factoriser (x-1)^{2}-4 à l’aide de l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) puisqu’il n’y a que deux termes ? Oui car (x-1)^{2}-4 est la différence de deux carrés.

a^{2}=(x-1)^{2} donc a=x-1

b^{2}=4 donc b=2

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}-b^{2}=(a-b)(a+b) 

(x-1)^{2}-4=((x-1)-2)((x-1)+2)\\\hspace{2cm}=(x-3)(x+1)

Ainsi    2(x-1)^{2}-8=2(x-3)(x+1) 

Factorisons 3(2x+1)^{2}+27 .

Y’a-t-il un facteur commun ? Oui : 3.

3(2x+1)^{2}={3}\times{(2x+1)^{2}}

27={3}\times{9}

3(2x+1)^{2}+27=3((2x+1)^{2}+9)

Peut-on factoriser (2x+1)^{2}+9 à l’aide de l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) puisqu’il n’y a que deux termes ? Non car (2x+1)^{2}+9 n’est pas la différence de deux carrés, c’est une somme.

Factorisons 5(3x+1)^{2}-45 .

Y’a-t-il un facteur commun ? Oui :5.

5(3x+1)^{2}={5}\times{(3x+1)^{2}}

\hspace{1.2cm}45={5}\times{9}

5(3x+1)^{2}-45=5((3x+1)^{2}-9)

Peut-on factoriser (3x+1)^{2}-9 à l’aide de l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) puisqu’il n’y a que deux termes ? Oui car (3x+1)^{2}-9 est la différence de deux carrés.

a^{2}=(3x+1)^{2} donc a=(3x+1)

b^{2}=9 donc b=3

Il ne reste plus qu’à remplacer a^{2}, b^{2}, a et b par leurs valeurs dans a^{2}-b^{2}=(a-b)(a+b) 

(3x+1)^{2}-9=((3x+1)-3)((3x+1)+3)\\\hspace{2.1cm}=(3x-2)(3x+4)

 

Ainsi    5(3x+1)^{2}-45=5(3x-2)(3x+4) 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.