Sommaire
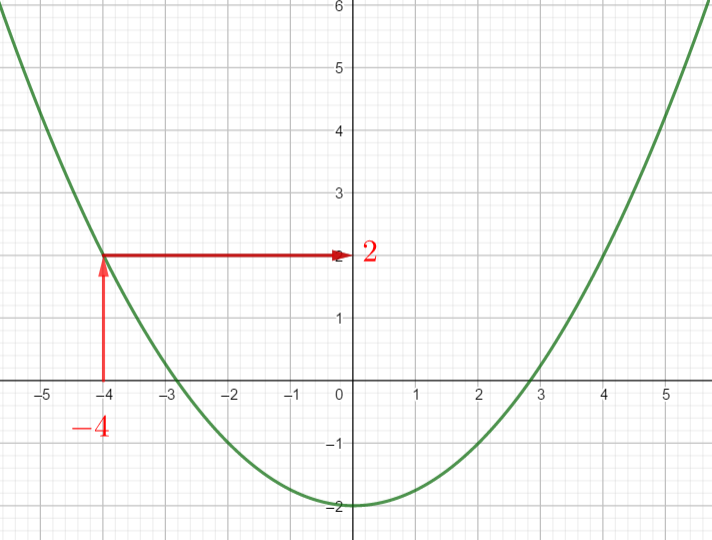
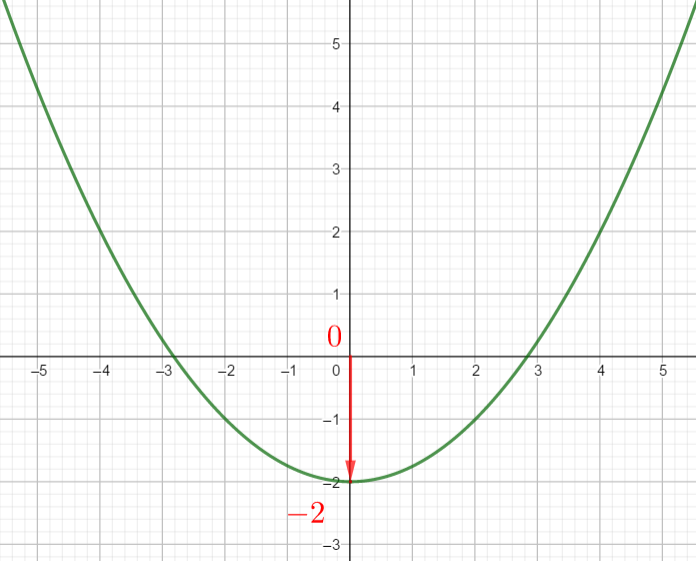
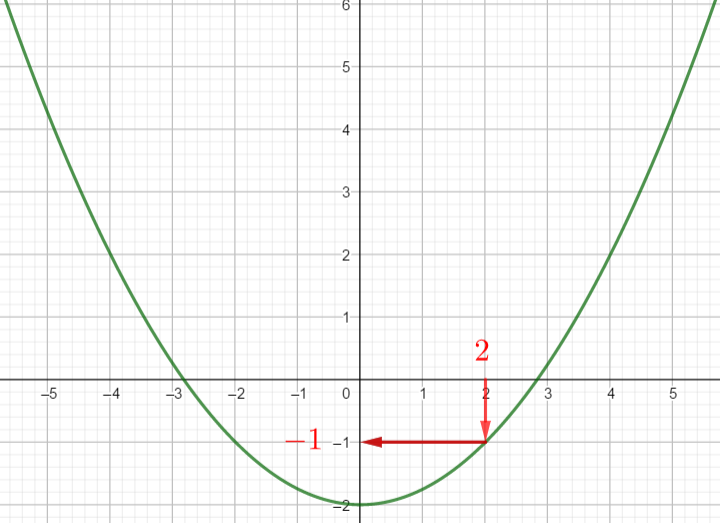
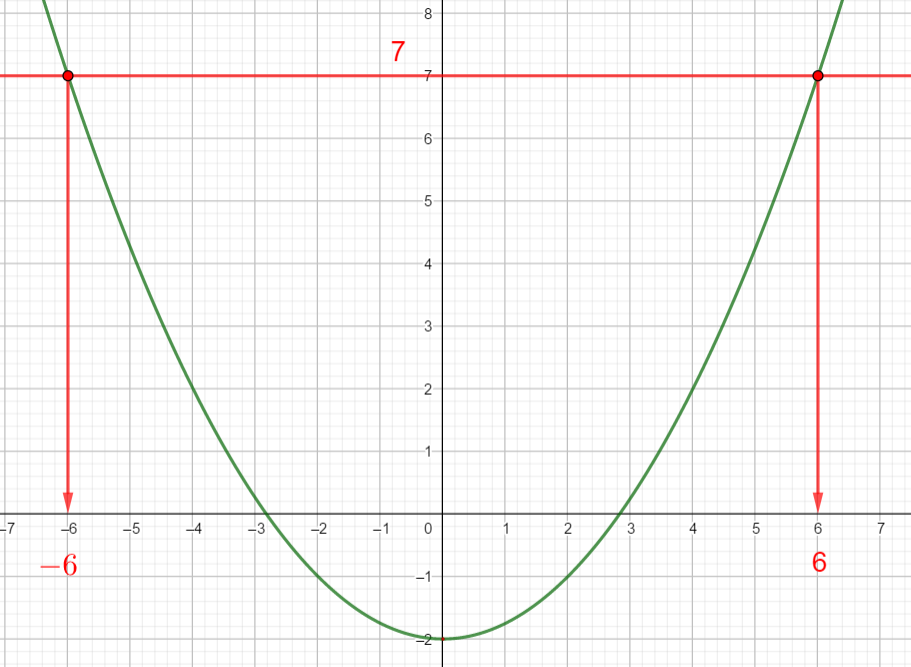
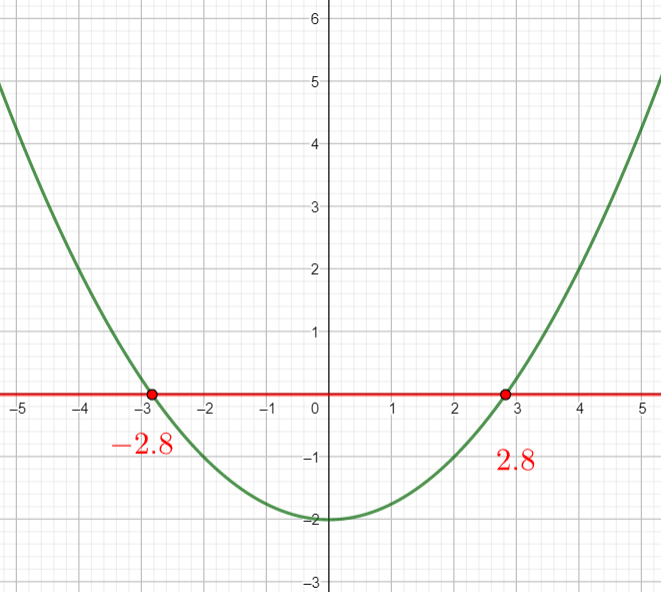
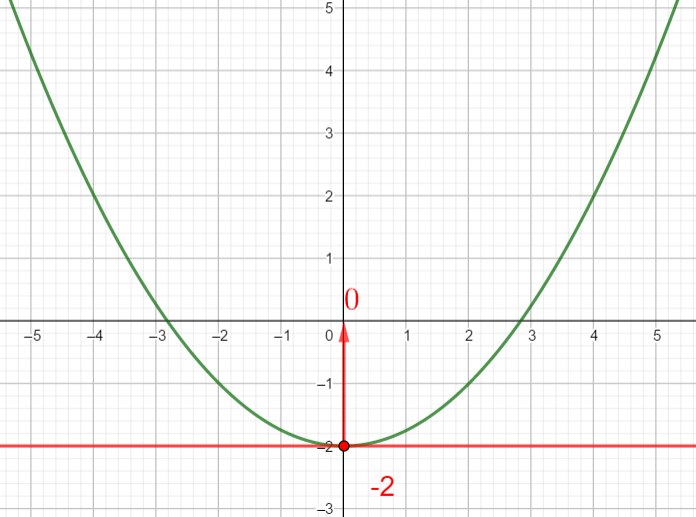
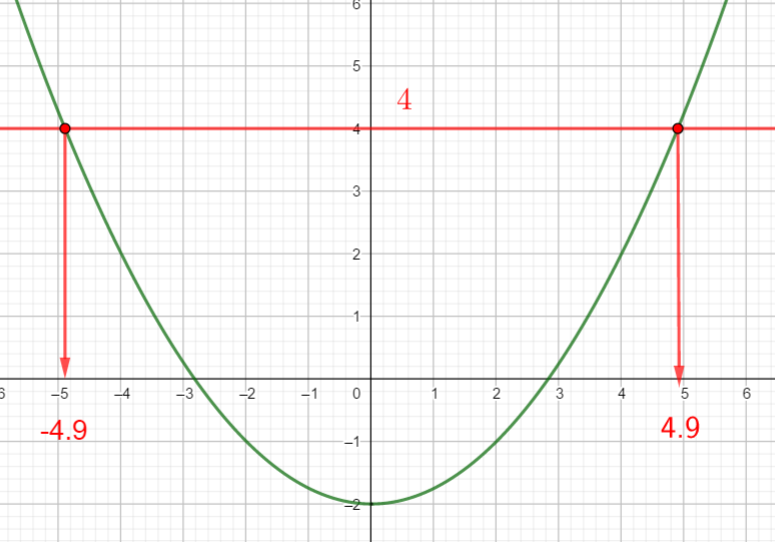
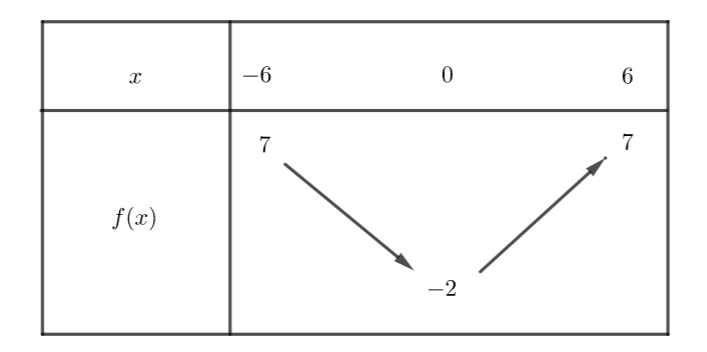
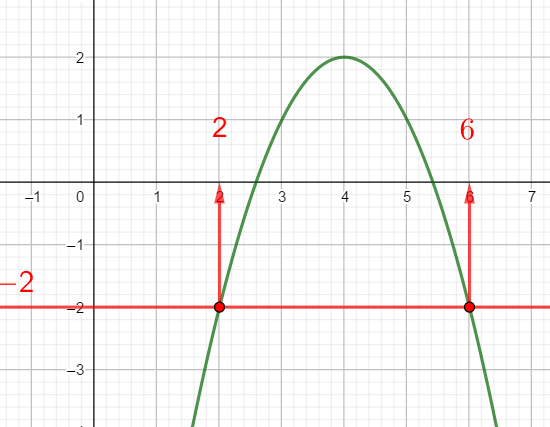
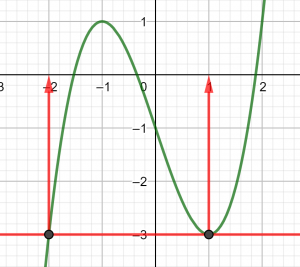
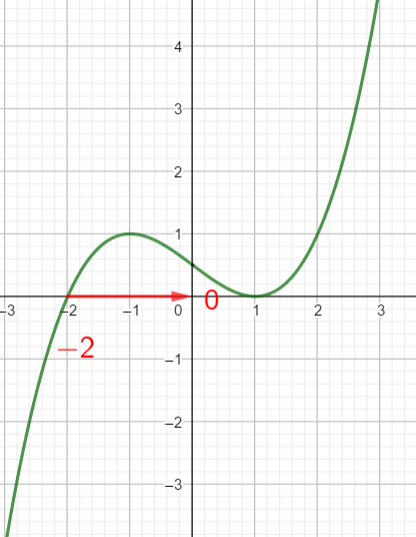
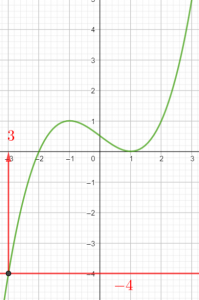
Exercice n°1
Voici la courbe d’une fonction f ci-dessous :
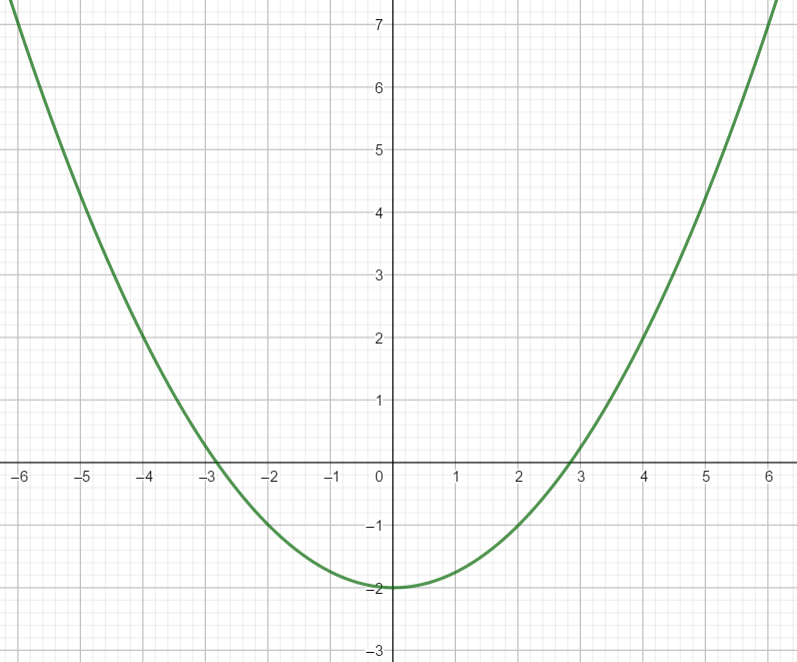
1) Déterminer graphiquement les images de -4 ; 0 et 2 .
2) a) Déterminer graphiquement le ou les antécédent(s) éventuels de 7 ; 0 et -2 .
b) Résoudre f(x)=4
3) Dresser le tableau de variations de f sur l’intervalle [-6;6]
4) La fonction admet-elle un minimum ? Si oui, pour quelle valeur de x ?
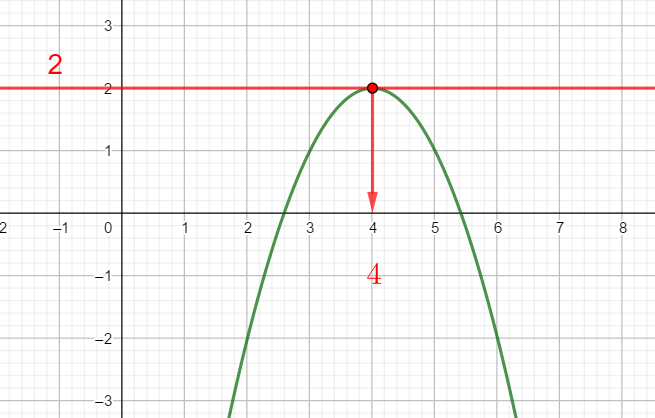
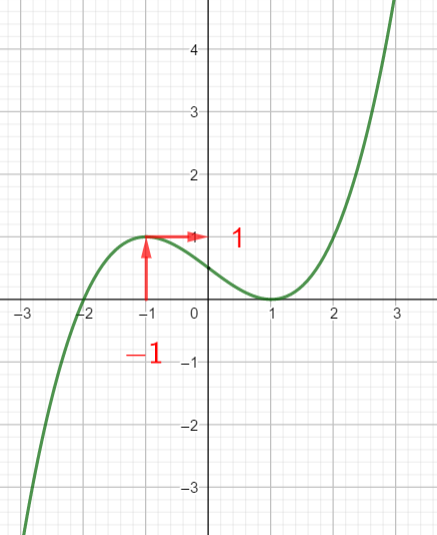
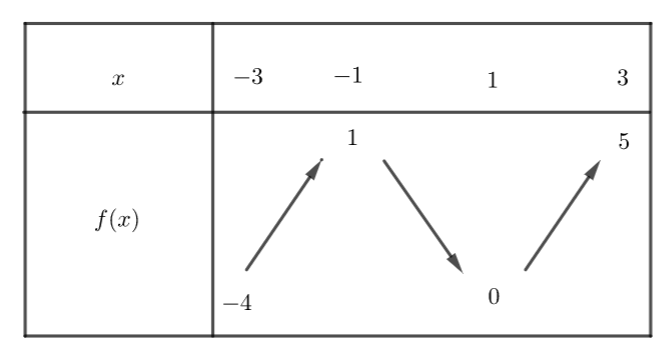
Exercice n°2
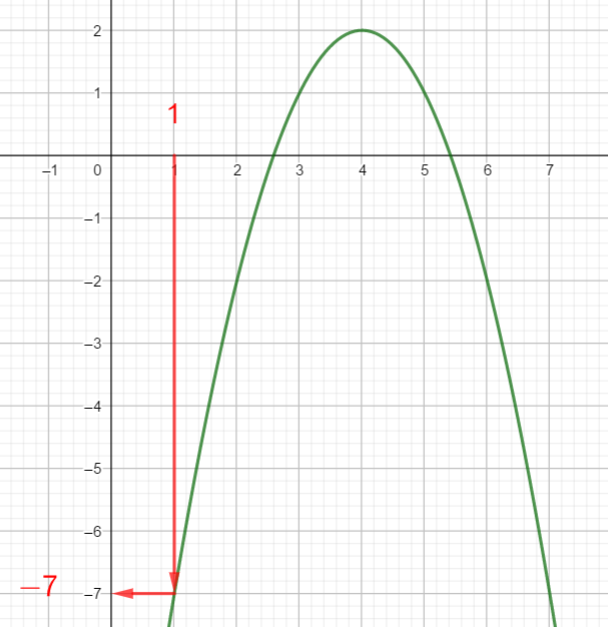
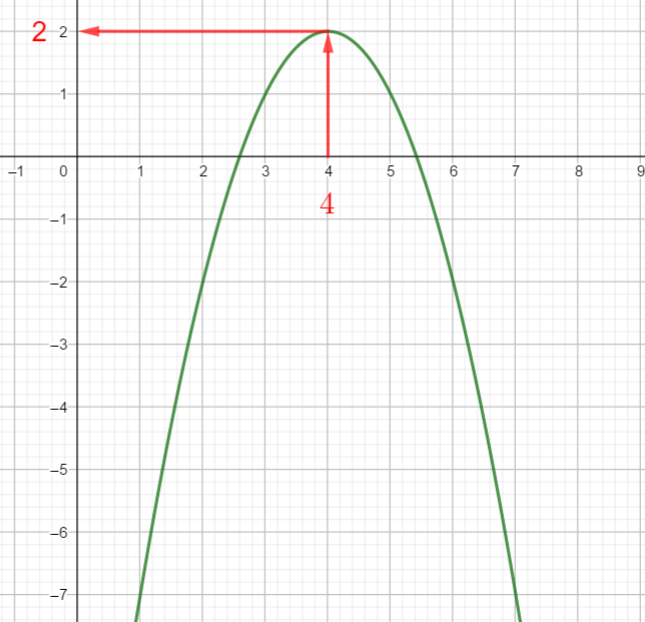
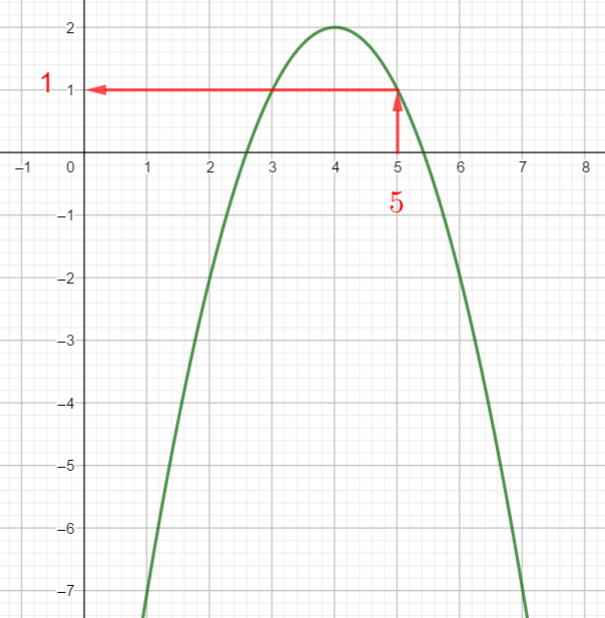
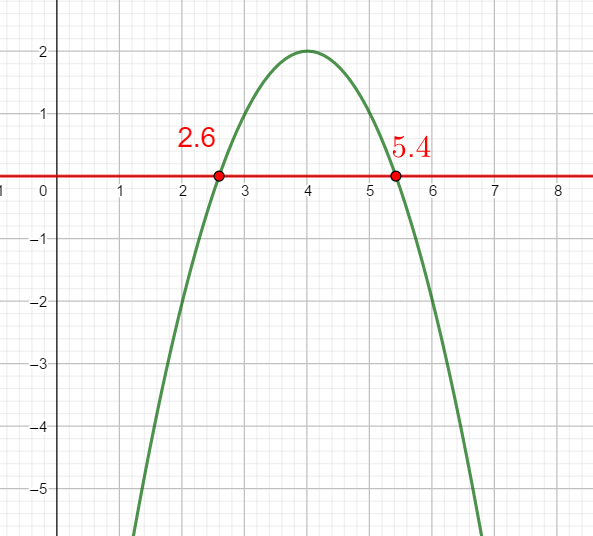
Voici la courbe de la fonction f
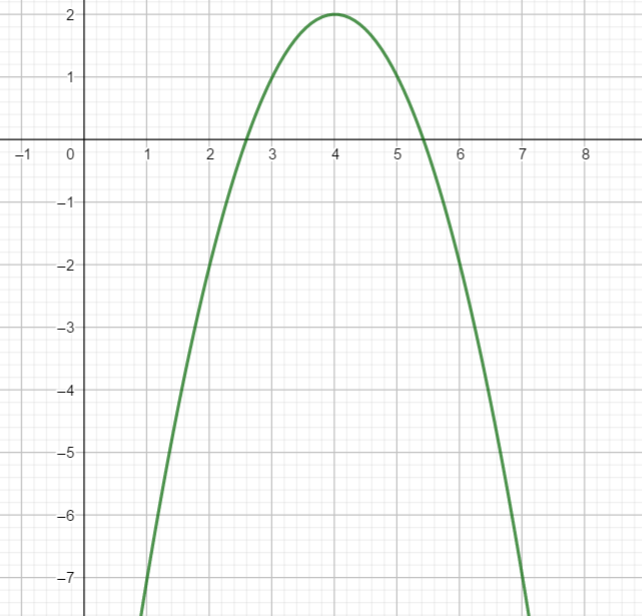
1) Déterminer graphiquement les images de 1 ; 4 et 5 .
2) a) Déterminer graphiquement le ou les antécédent(s) éventuels de 0 et -2 .
b) Résoudre graphiquement f(x)=2
3) Dresser le tableau de variations de f sur l’intervalle [1;7]
4) La fonction admet-elle un maximum ? Si oui, pour quelle valeur de x ?
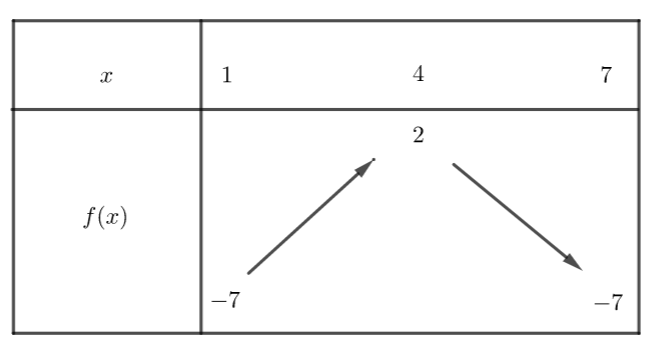
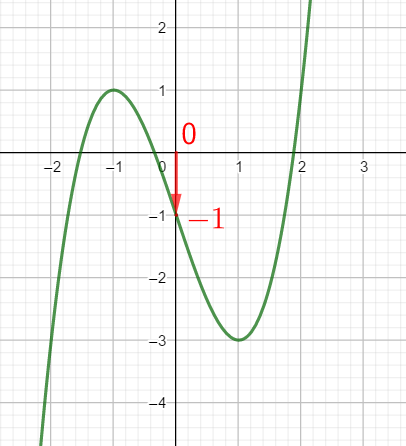
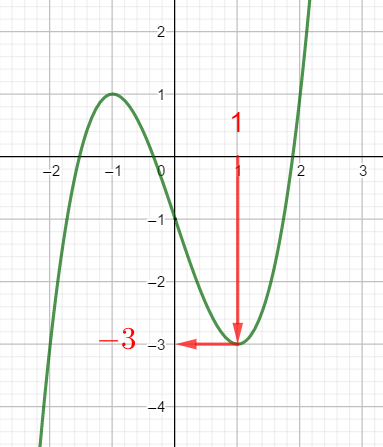
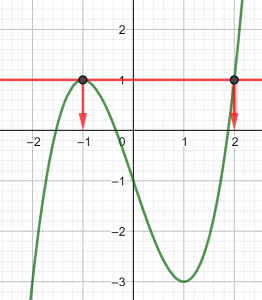
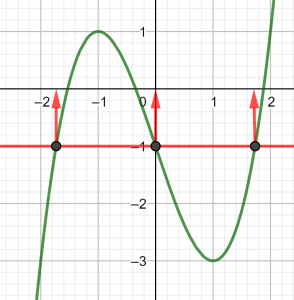
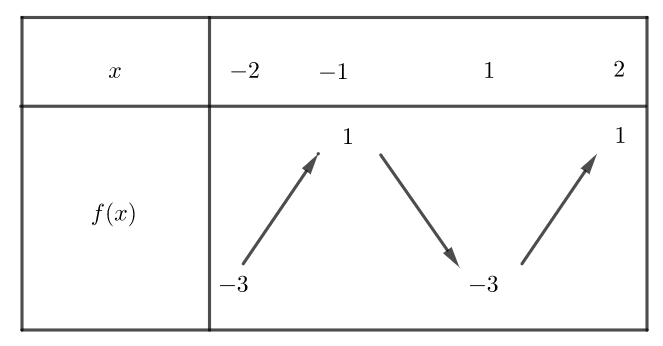
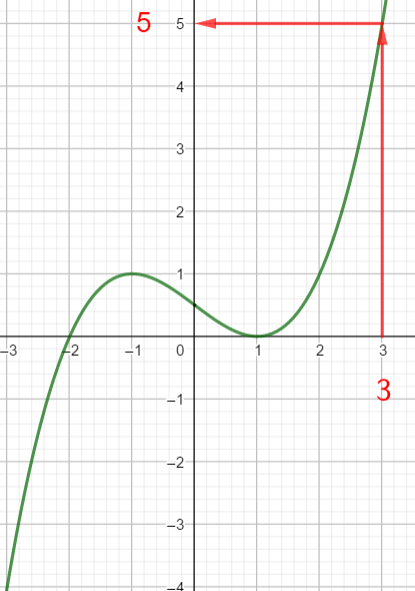
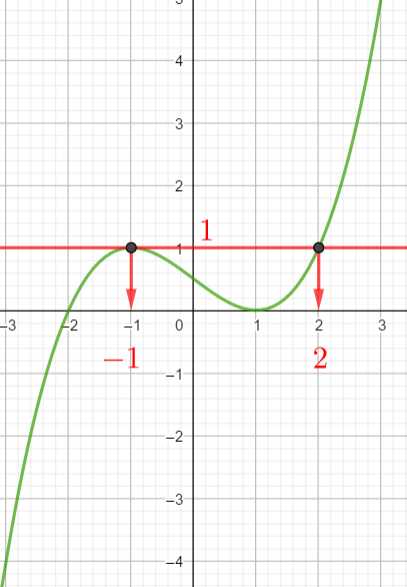
Exercice n°3
Voici la courbe de la fonction f
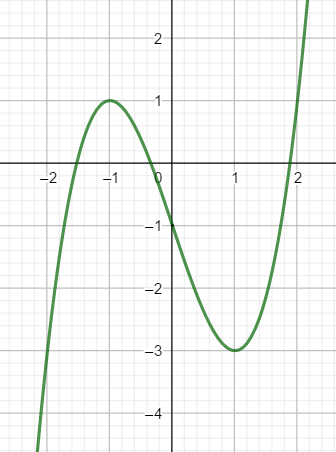
1) Déterminer graphiquement les images de -2 ; 0 et 1 .
2) a) Déterminer graphiquement le ou les antécédent(s) éventuels de 1 et -1 .
b) Résoudre graphiquement f(x)=-3
3) Dresser le tableau de variations de f sur l’intervalle [-2;2]
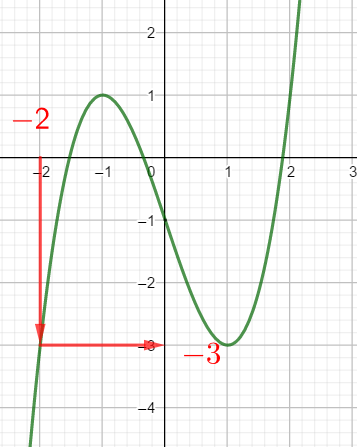
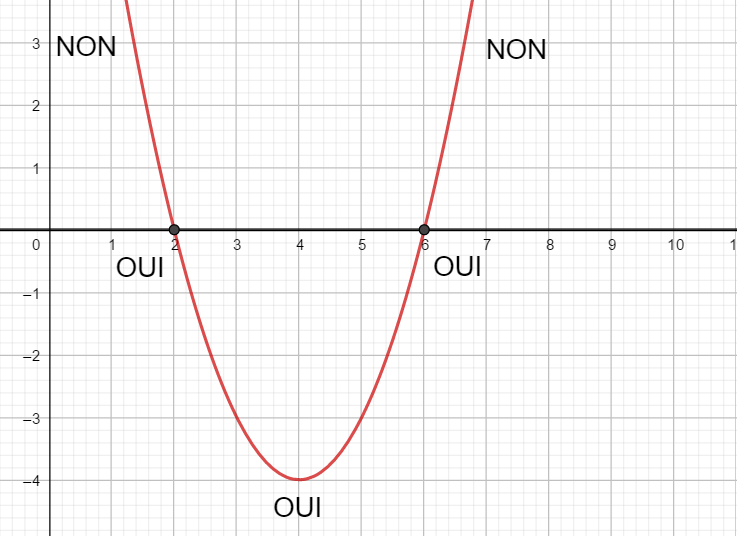
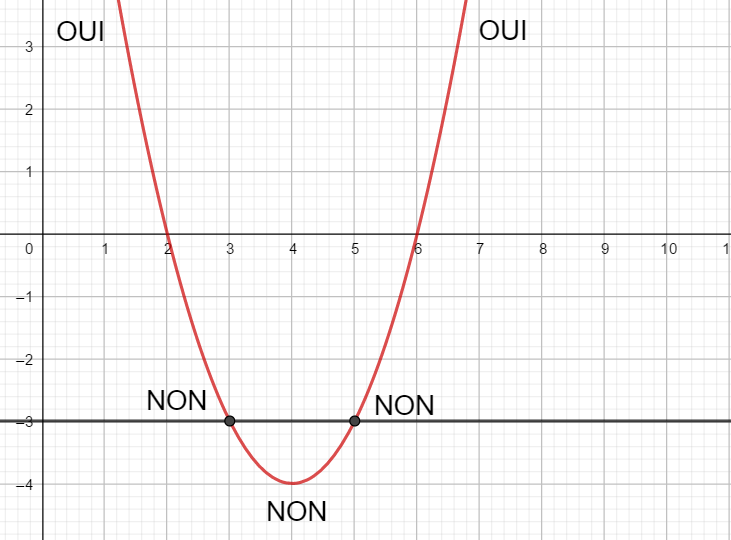
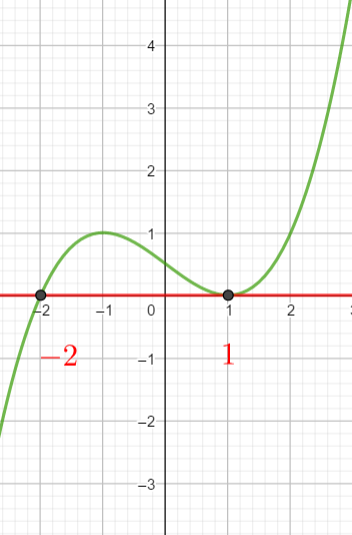
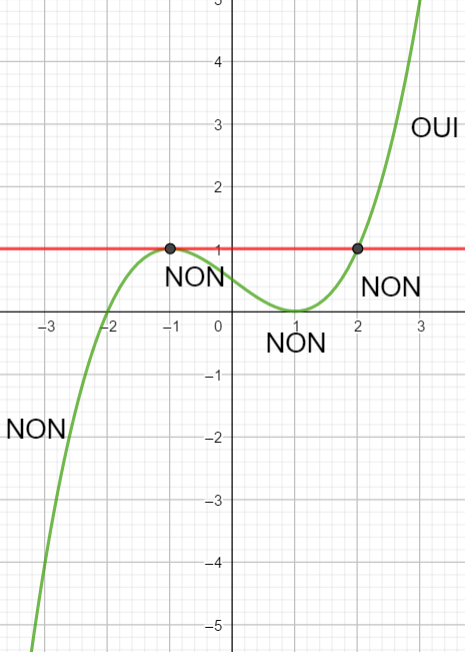
Exercice n°4
Voici la courbe de la fonction f
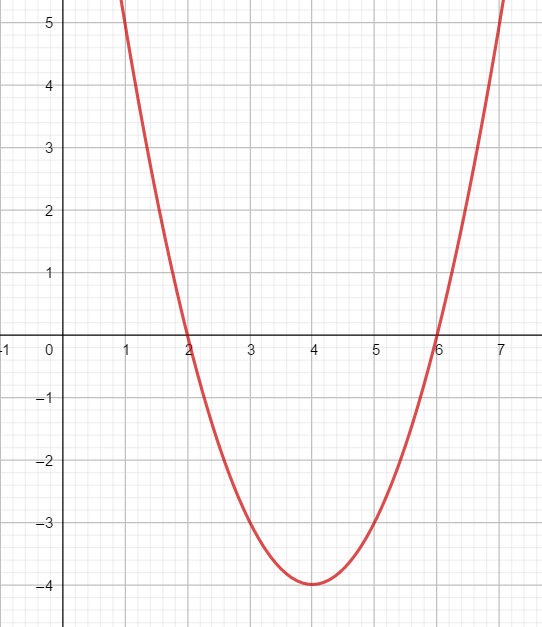
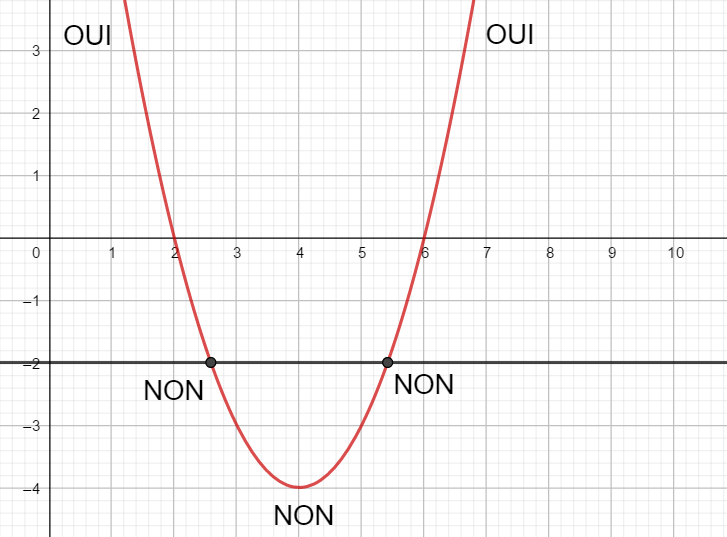
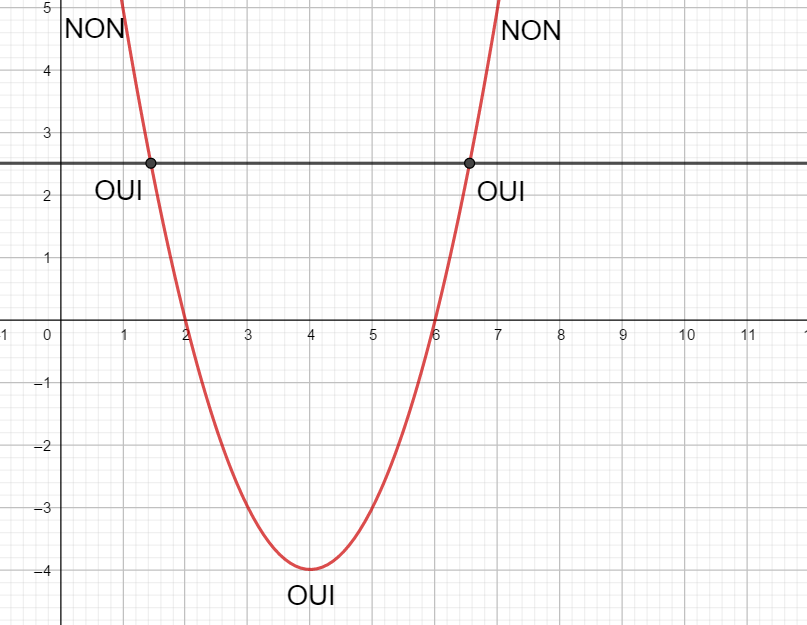
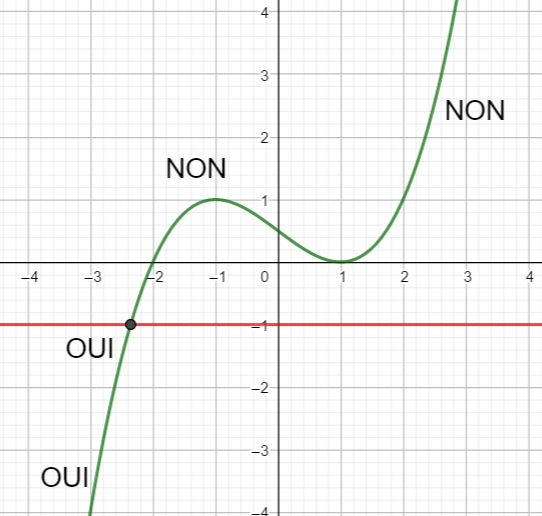
Résoudre les inéquations suivantes : f(x)\leq0 ; f(x)>-3 ; f(x)>-2 et f(x)\leq 2.5
Exercice n°5
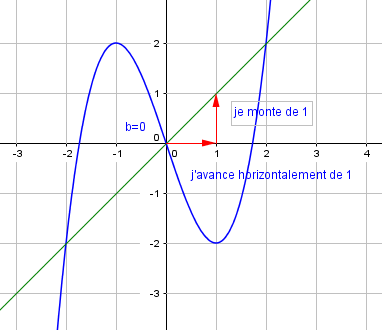
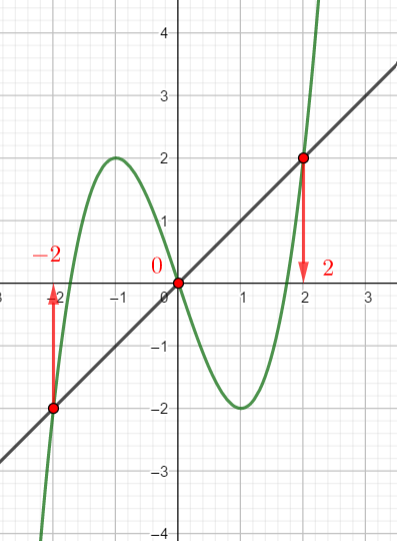
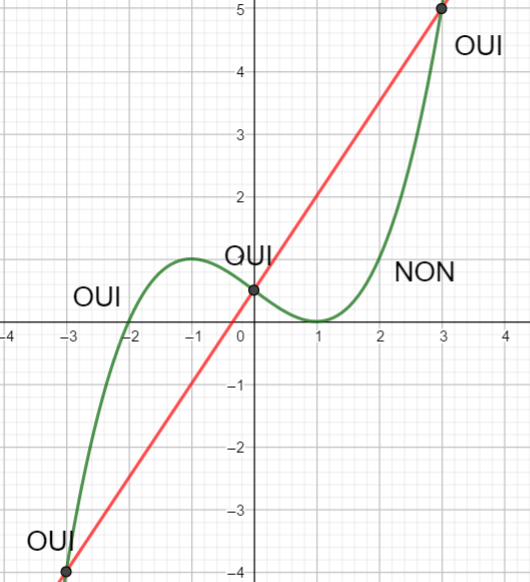
Voici la courbe de la fonction f
- Tracer, dans le repère, la droite D d’équation y=x en saisissant y=x dans la colonne Algèbre située à gauche de la page géogébra ci-dessus.
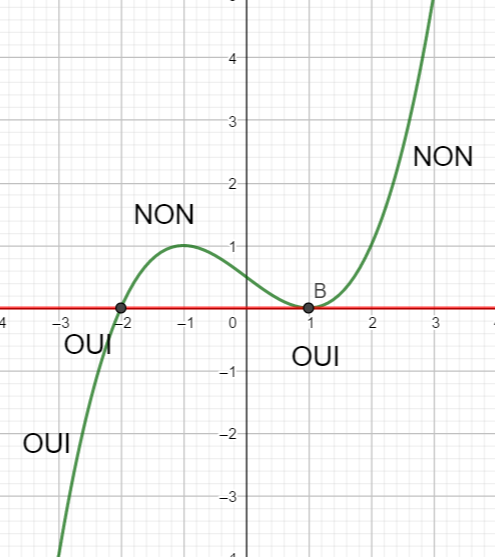
2. Résoudre f(x)=x
3. Résoudre f(x)\geq x
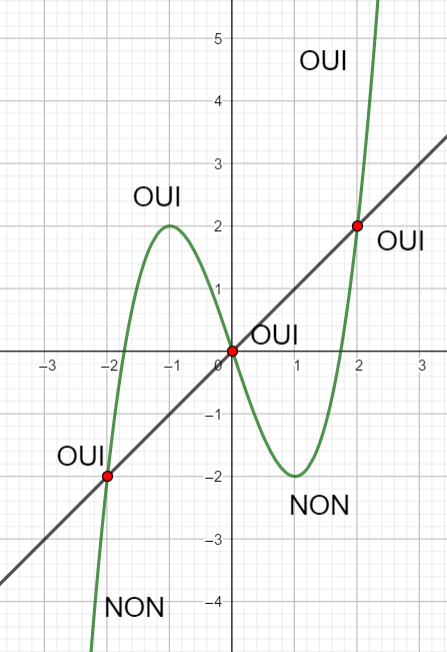
Exercice n°6
Voici la courbe de la fonction f
- Tracer la droite D d’équation y=-x+4 en saisissant y=-x+4 dans la colonne Algèbre située à gauche de la page géogébra ci-dessus.
2. Résoudre graphiquement f(x)=-x+4
3. Résoudre graphiquement f(x)>-x+4
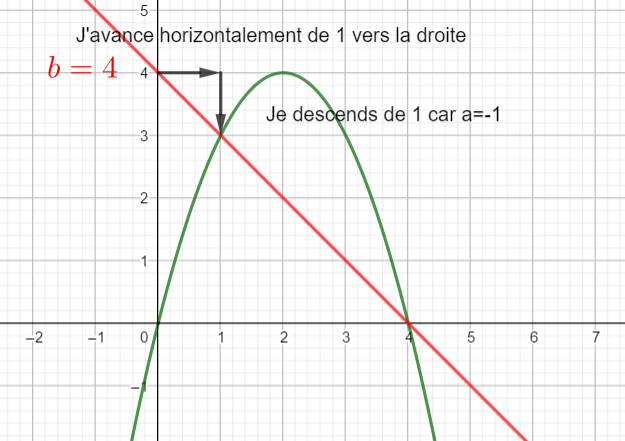
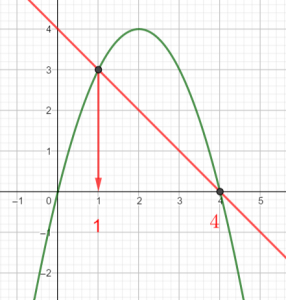
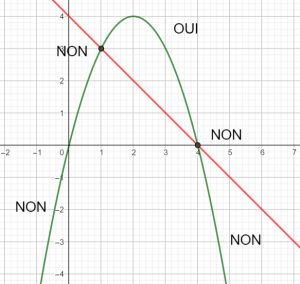
Exercice n°7
Voici la courbe de la fonction f
- Sur quel ensemble est définie la fonction f ?
2) Déterminer graphiquement les images de -2 ; -1 et 3 .
3) a) Déterminer graphiquement le ou les antécédent(s) éventuels de 0 et -4 .
b) Résoudre graphiquement f(x)=1
4) Dresser le tableau de variations de f sur l’intervalle [-3;3]
5) Résoudre les inéquations suivantes : f(x)>1 ; f(x)\leq-1 et f(x)\leq 0
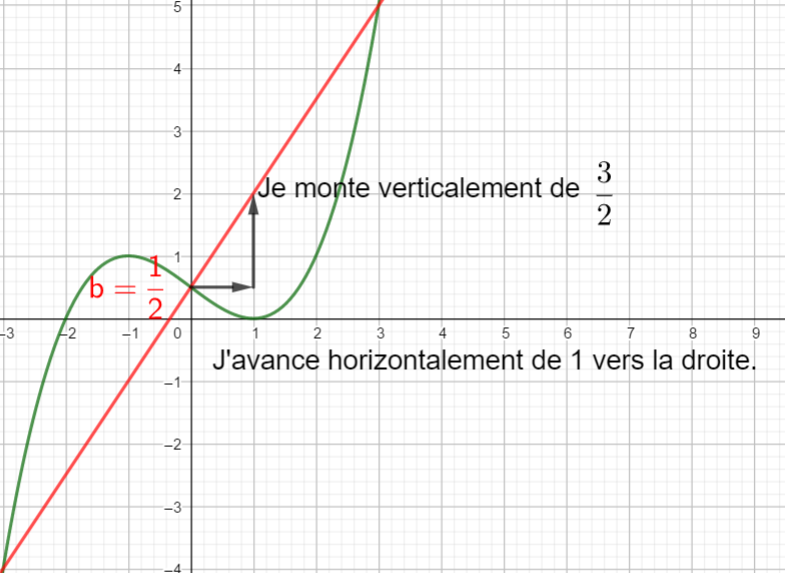
6)a) tracer la droite d’équation y=\frac{3 }{2}x+\frac{1}{2} en saisissant y=\frac{3 }{2}x+\frac{1}{2} dans la colonne Algèbre située à gauche de la page géogébra ci-dessus..
6)b) Résoudre f(x)=\frac{3 }{2}x+\frac{1}{2}.
6)c) Résoudre f(x)\geq\frac{3 }{2}x+\frac{1}{2}.
Exercice n°8
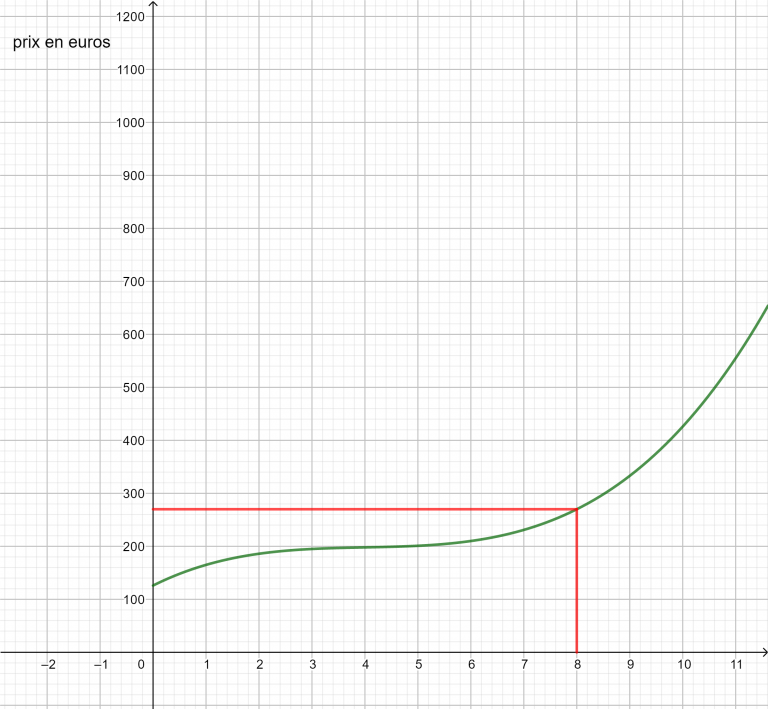
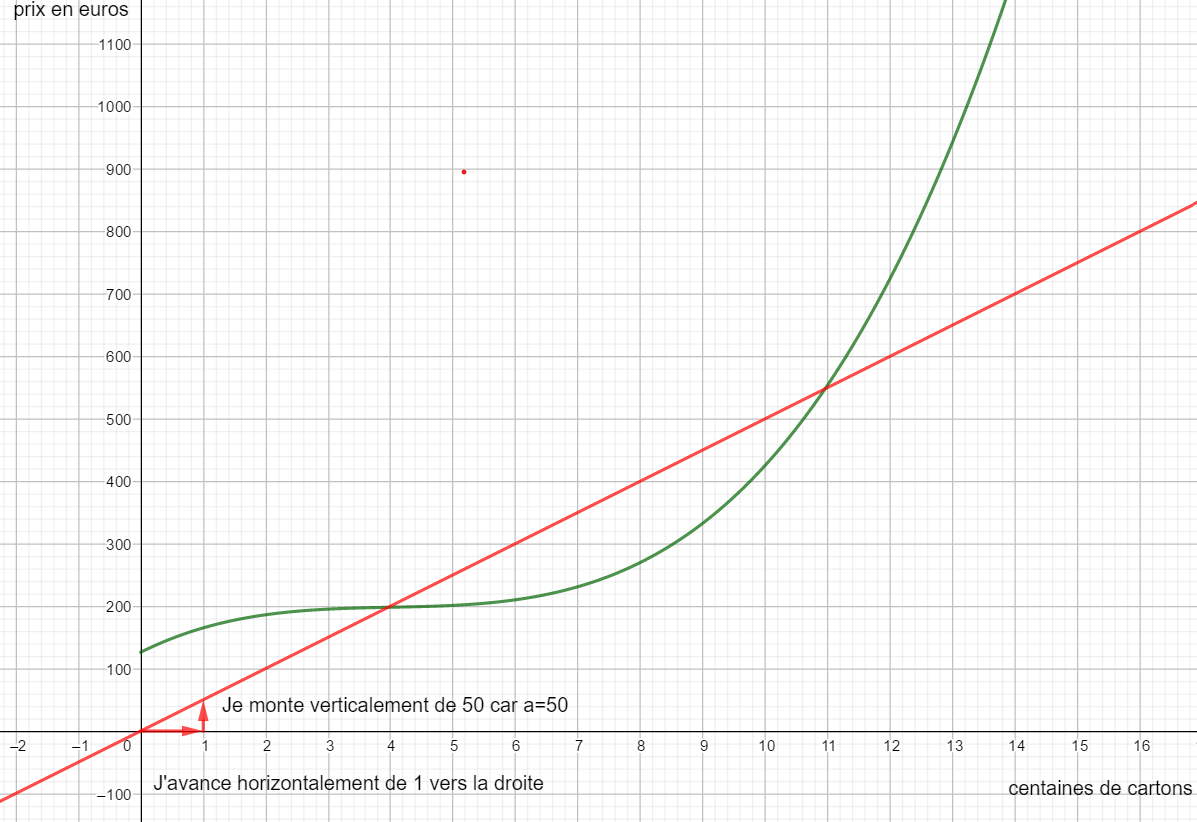
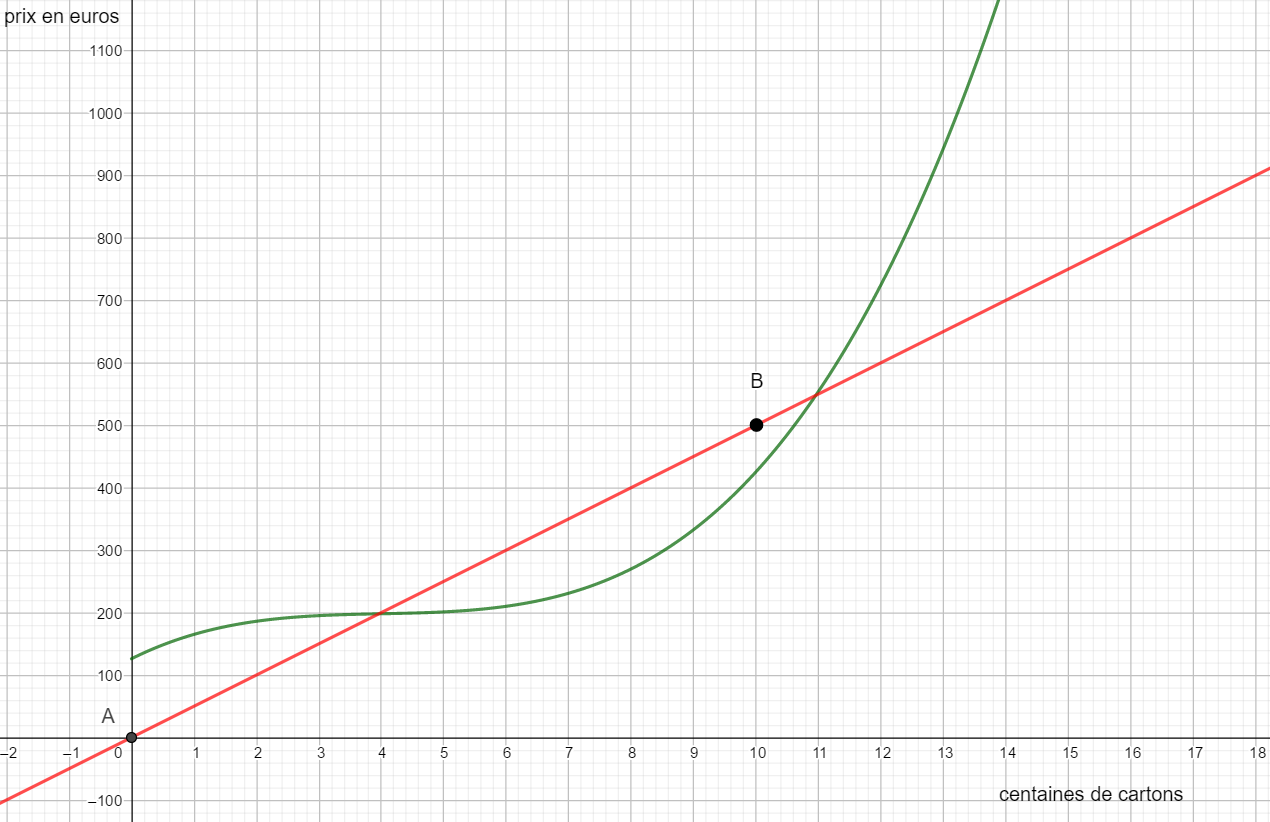
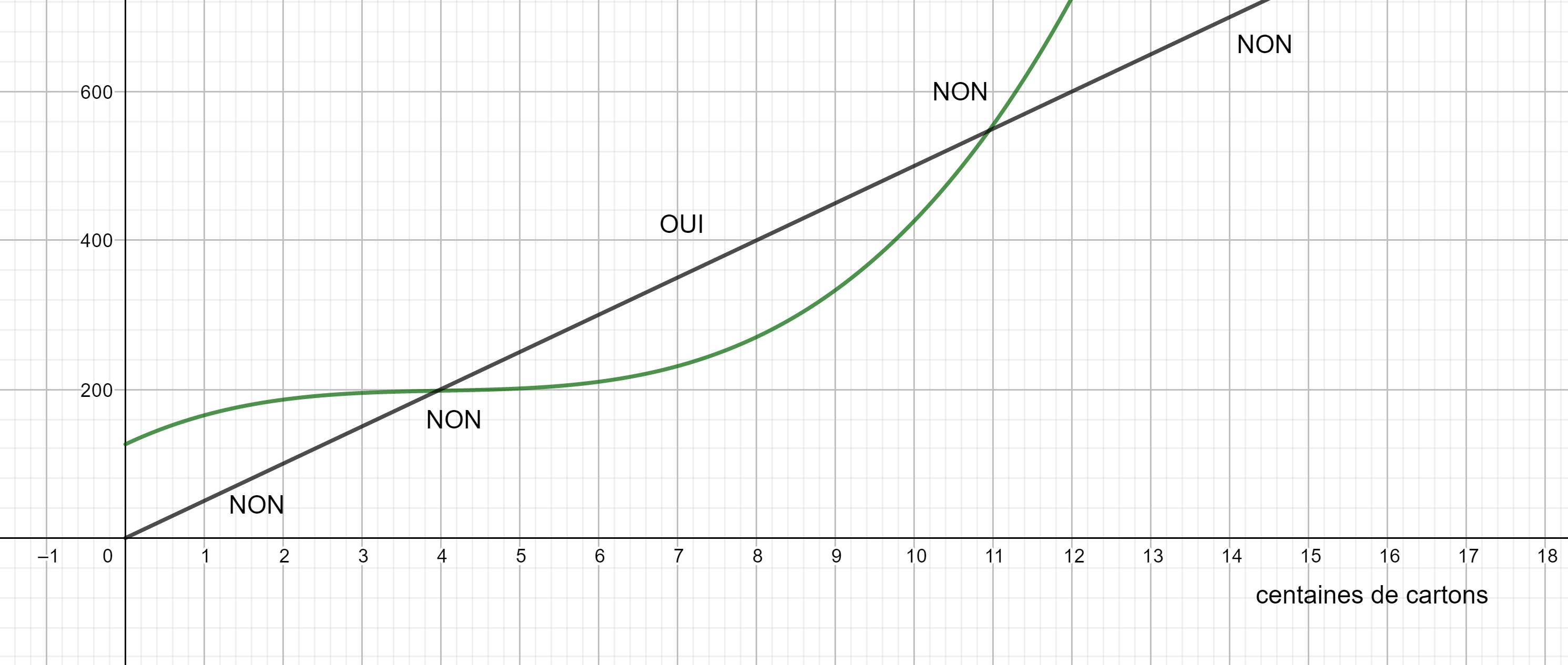
Chaque jour une petite entreprise fabrique des cartons d’emballage.La courbe ci-dessous représente le coût de fabrication f(x) pour x centaines de cartons.
- Déterminer graphiquement le coût de fabrication pour 8 centaines de cartons et pour 12 centaines de cartons.
2. Déterminer graphiquement combien de centaines de cartons peut-on fabriquer avec 210 euros ?
3. On suppose que toute la production est vendue au prix de 50 euros la centaine de cartons. La recette journalière est donnée par la formule R(x)=50x.
a. tracer la droite d’équation y=50x.
b. Déterminer graphiquement combien de centaines cartons doit fabriquer l’entreprise pour qu’elle réalise un bénéfice.
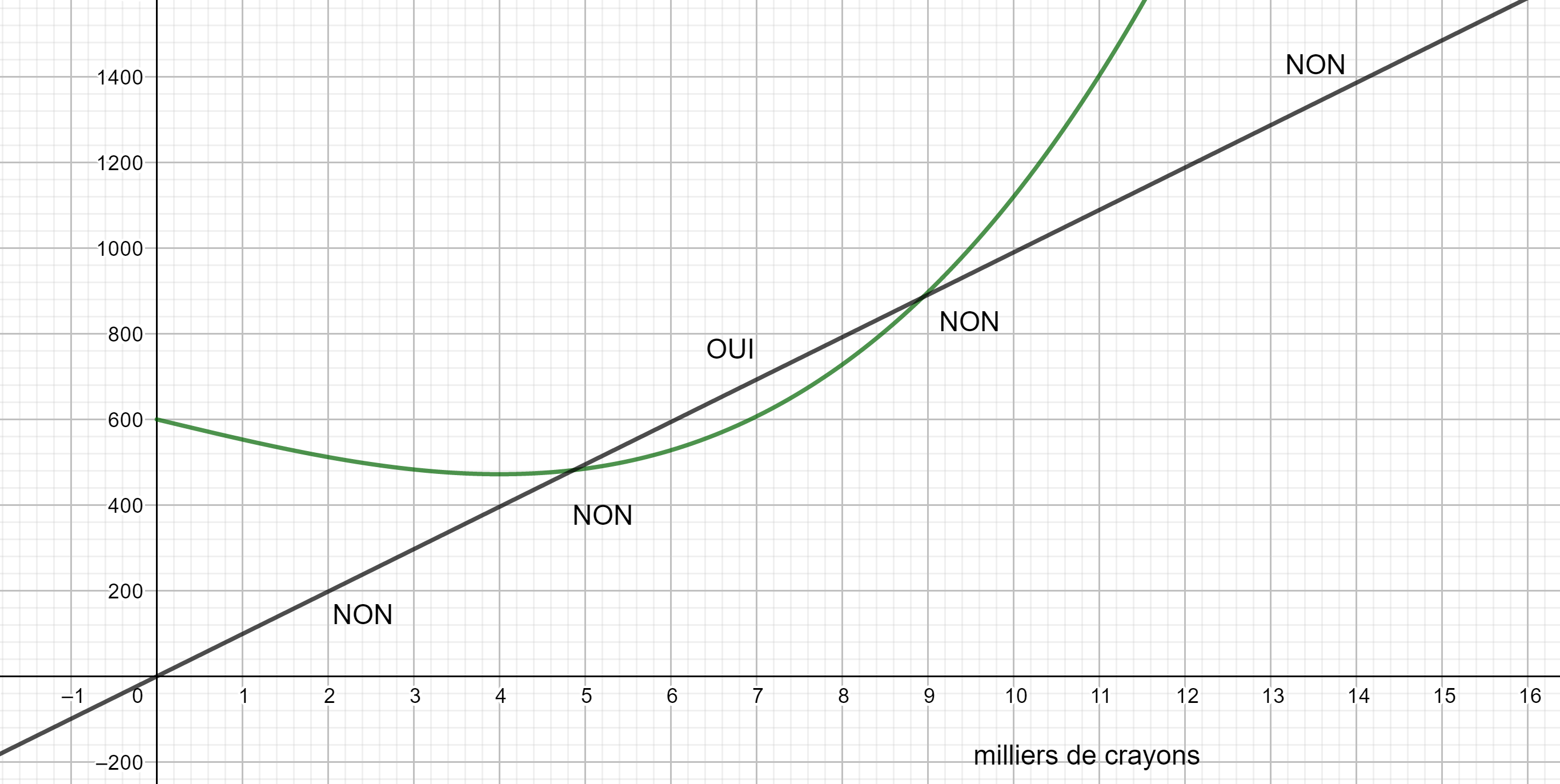
Exercice n°9 :
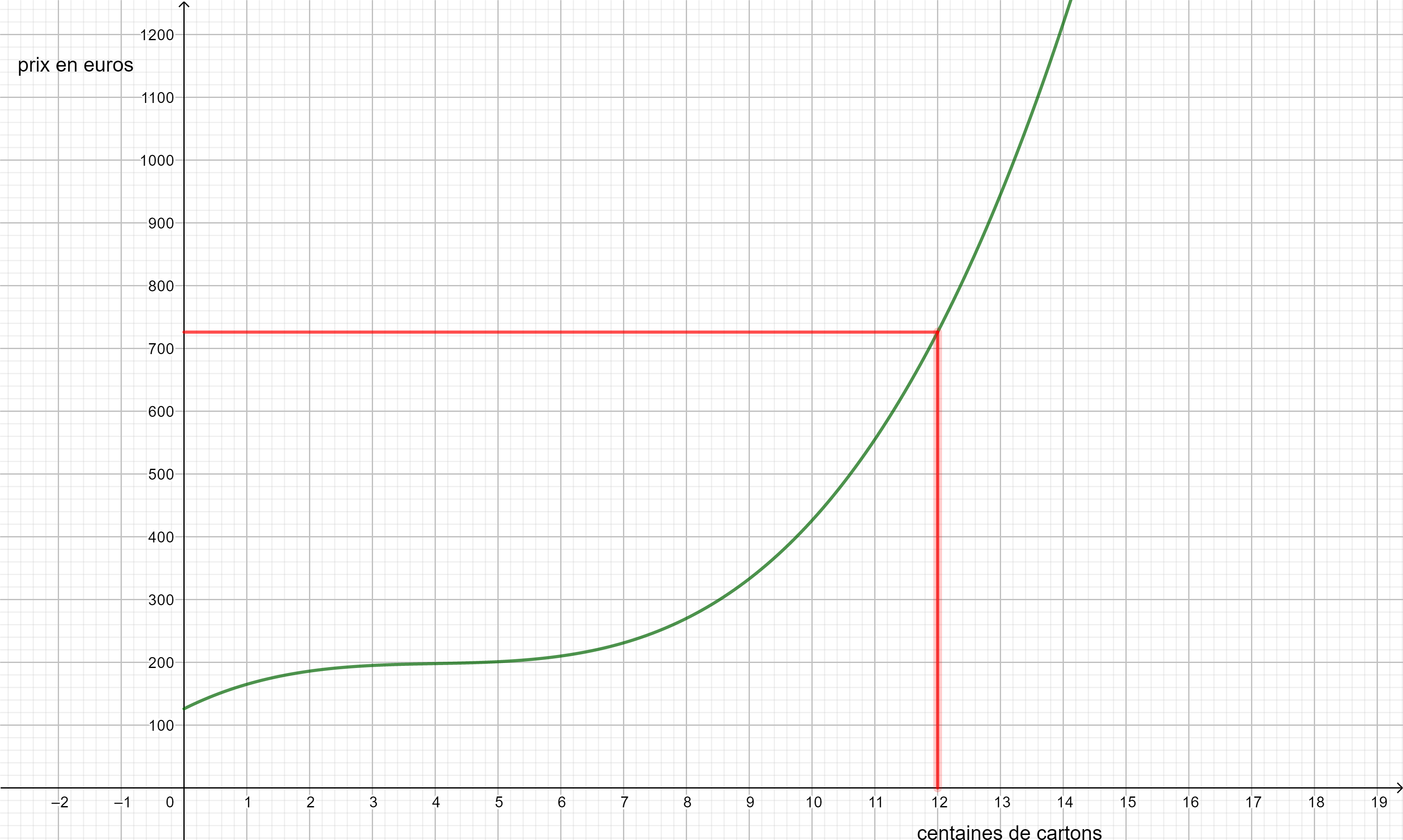
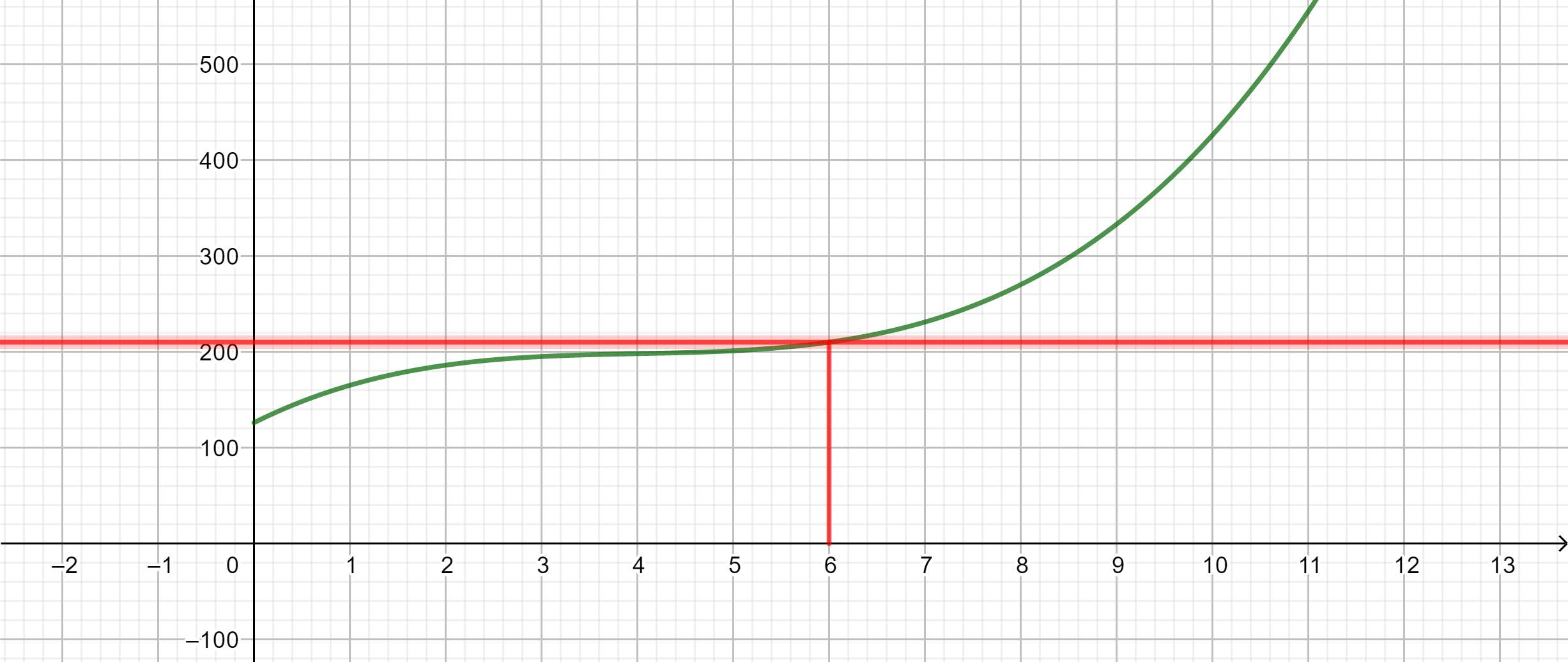
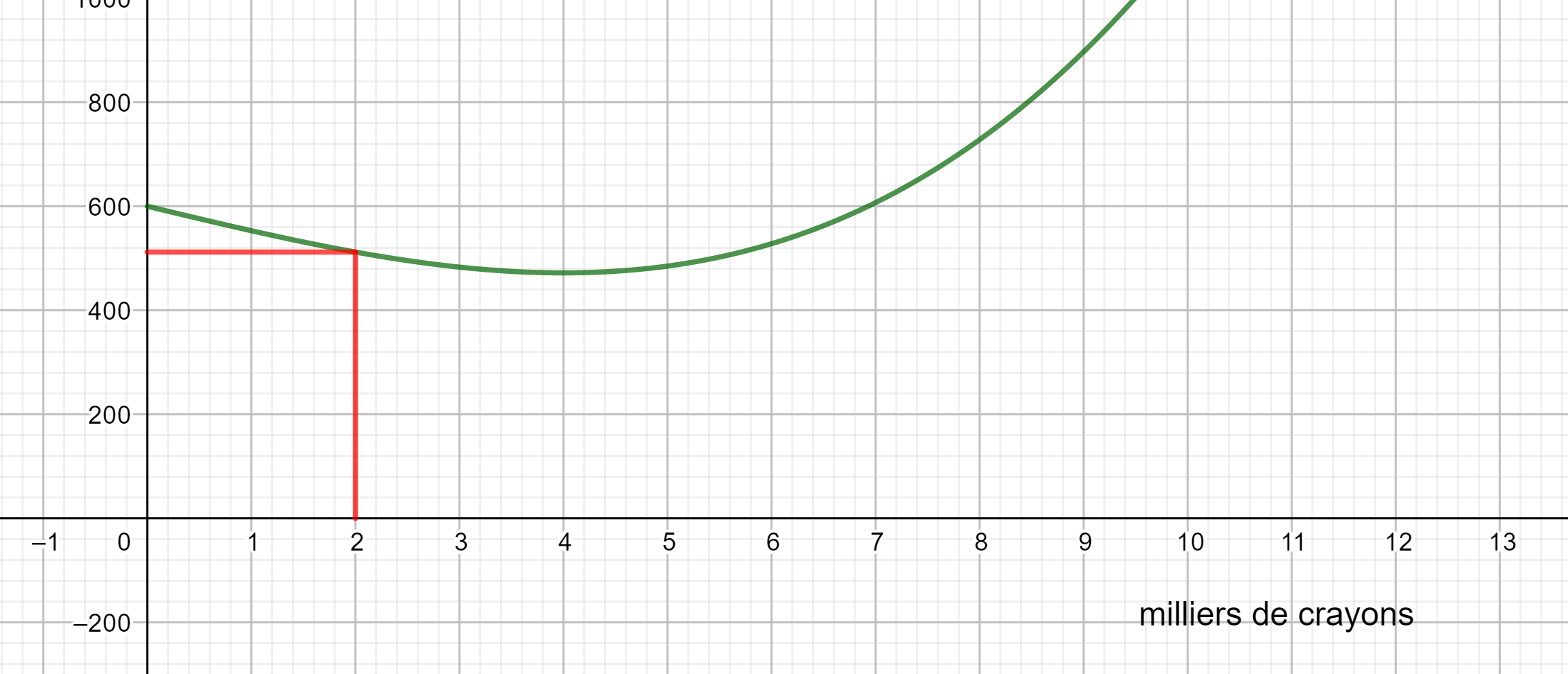
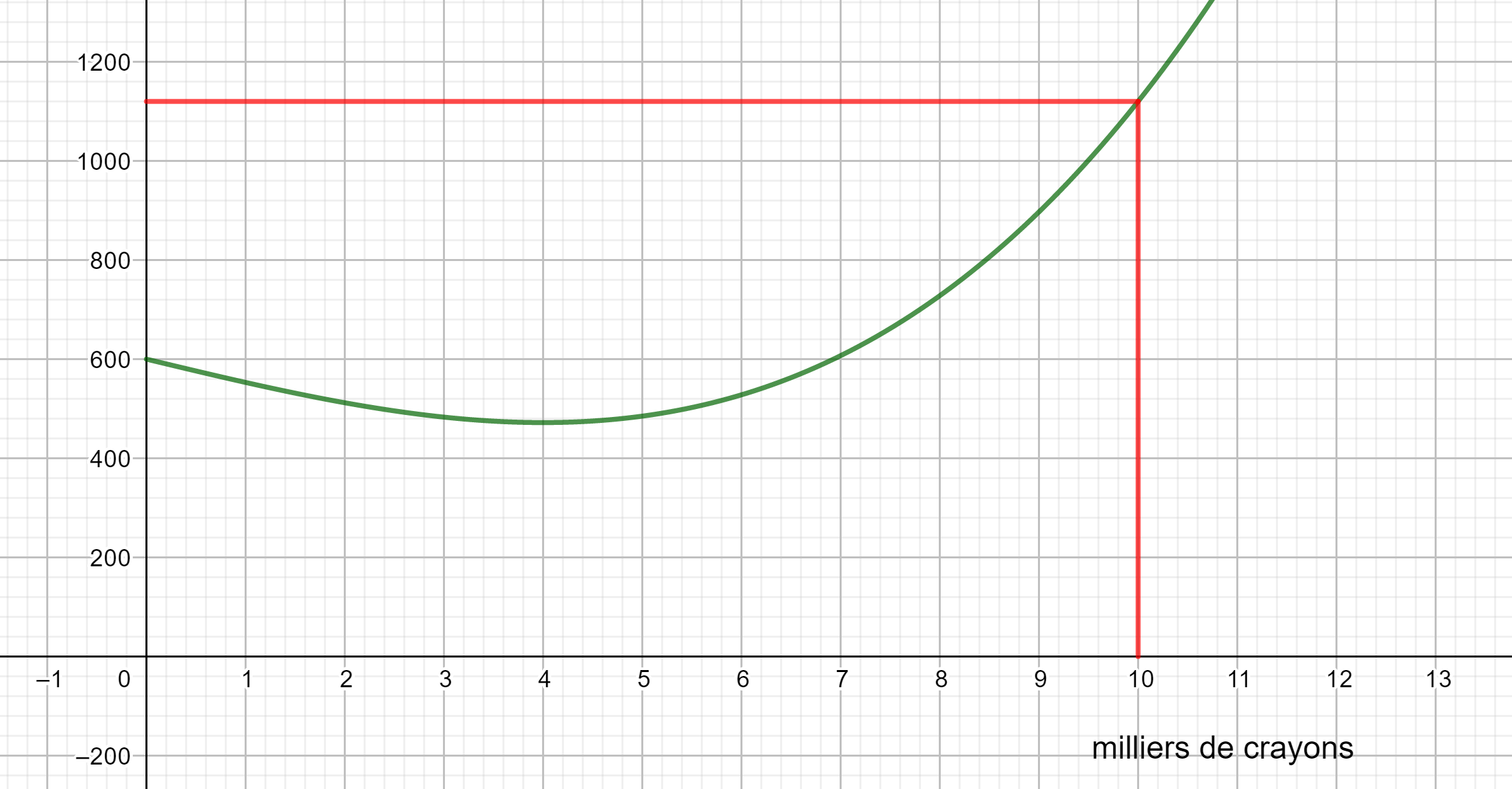
Une entreprise fabrique des crayons de couleur. Le coût de production en euros est donné par la courbe ci-dessous.
- Déterminer graphiquement le coût de fabrication pour 2 milliers de crayons de couleur et pour 10 milliers de crayons de couleur
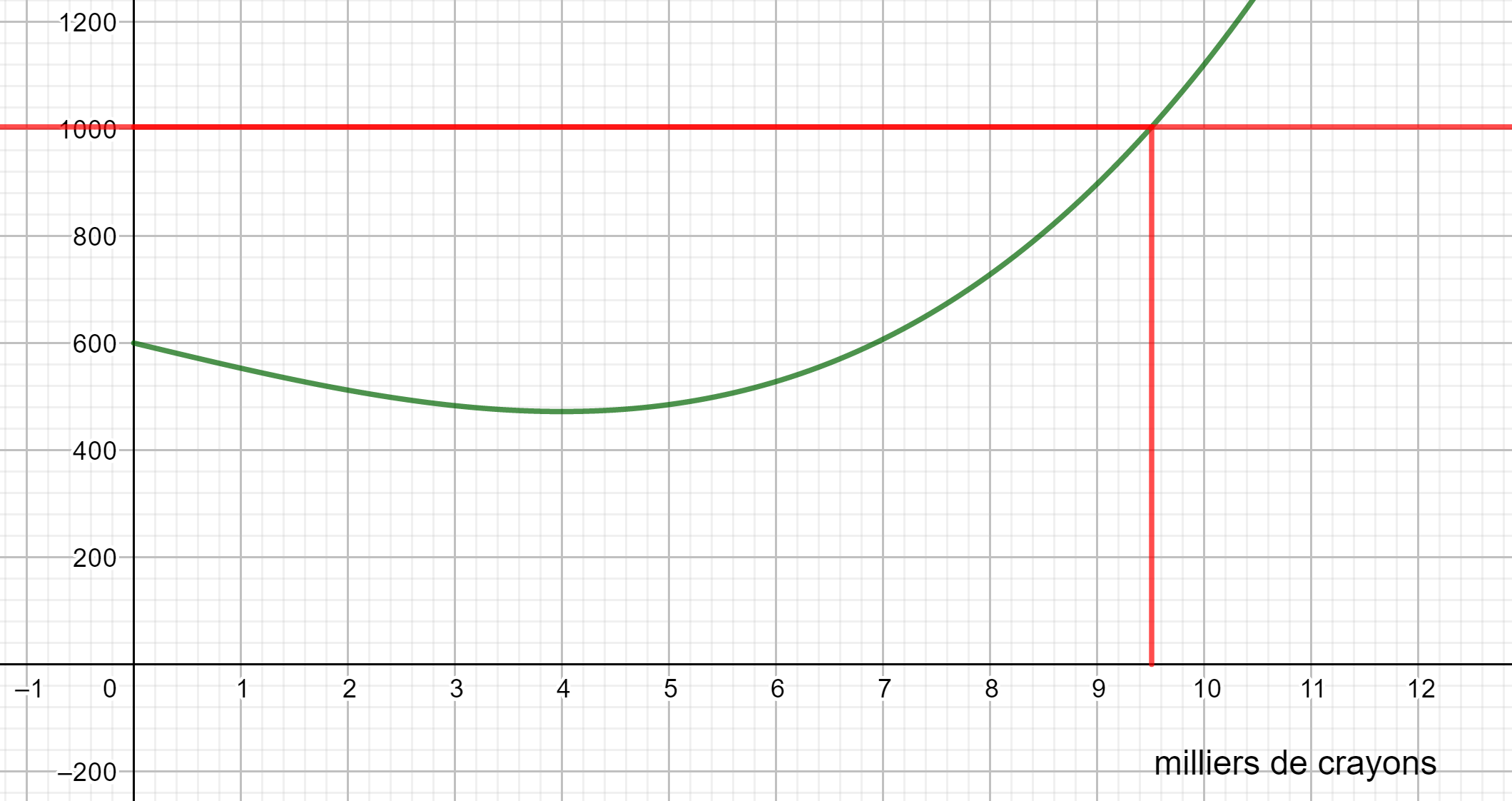
2. Déterminer graphiquement combien de milliers de crayons peut-on fabriquer avec 1000 euros ?
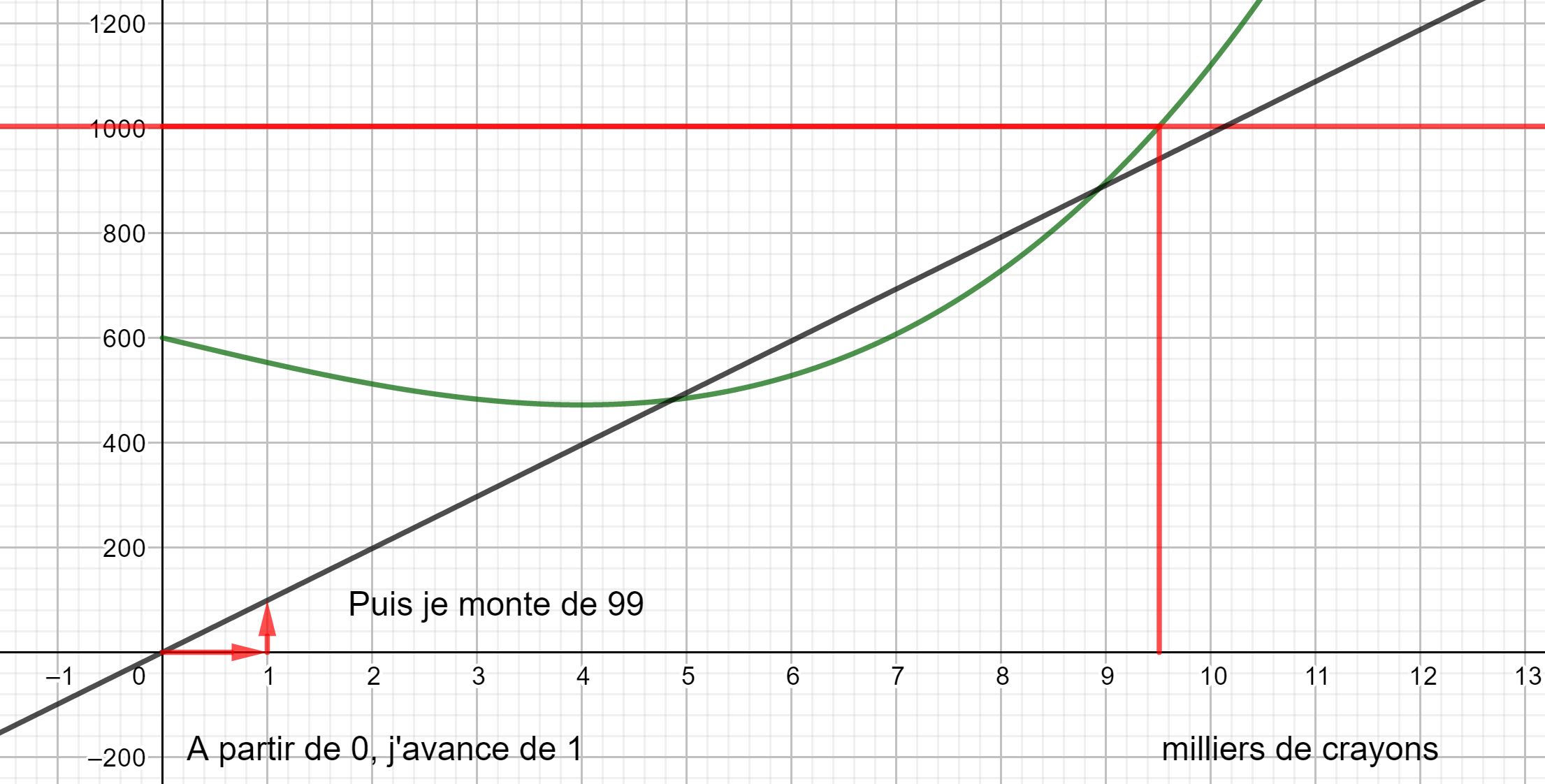
3. On suppose que toute la production est vendue au prix de 99 euros le millier de crayons. La recette journalière est donnée par la formule R(x)=99x.
a. tracer la droite d’équation y=99x en saisissant y=99x dans la colonne Algèbre située à gauche de la page géogébra ci-dessus.
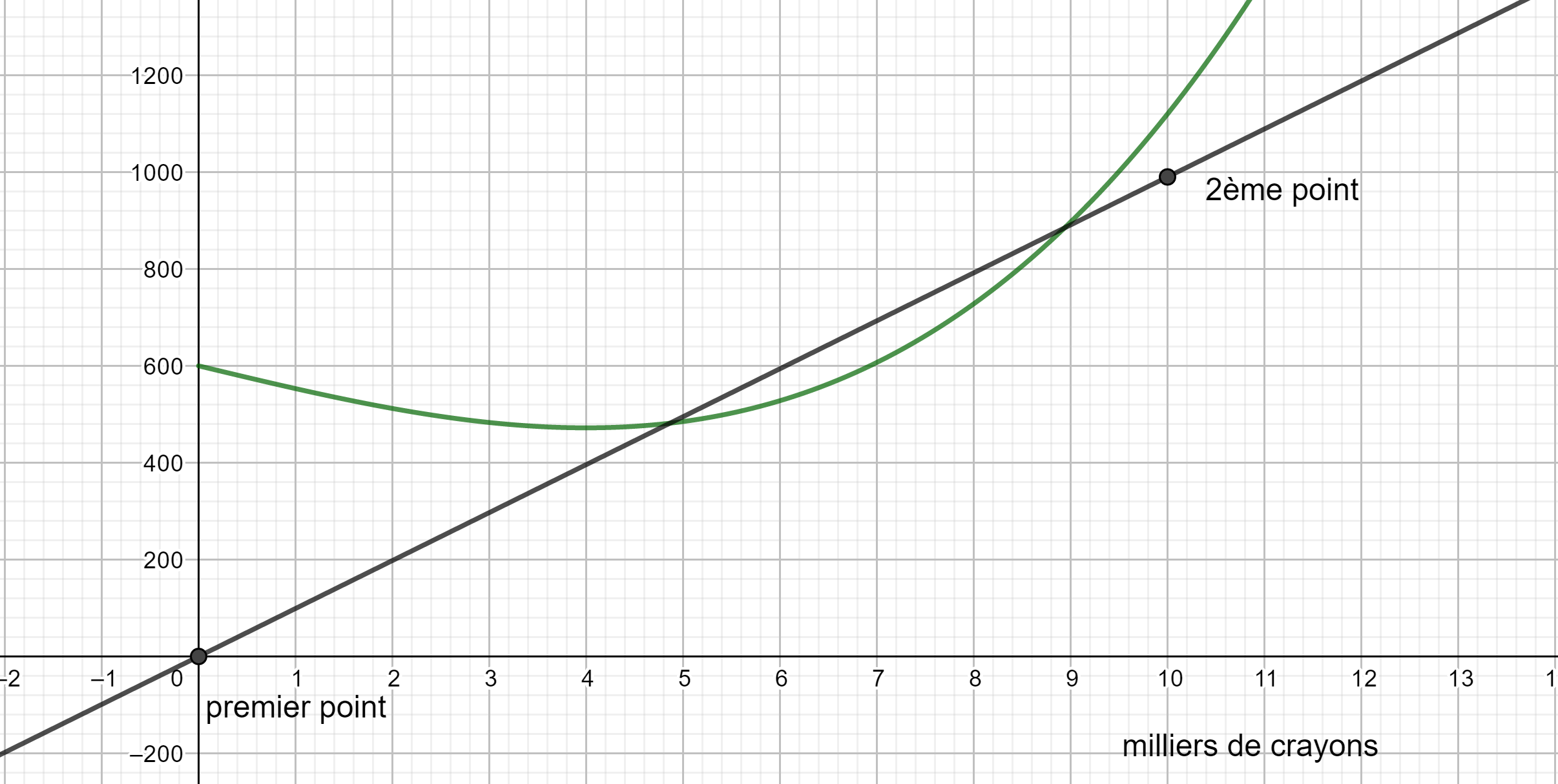
b. Déterminer graphiquement combien de milliers de crayons doit fabriquer l’entreprise pour qu’elle réalise un bénéfice.