logo

TS. Bac 22 suites exo1

Exercice n°1 Polynésie 4 mai 2022

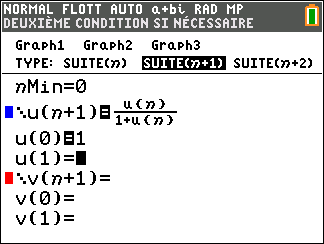
Soit (u_n) la suite définie par u_0=1 et pour tout entier naturel n

u_{n+1}=\frac{u_n}{1+u_n}

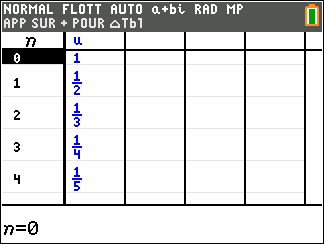
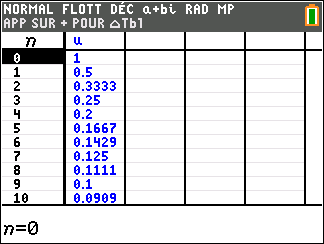
1. a. Calculer les termes u_1 , u_2 et u_3 . On donnera les résultats sous forme de fractions irréductibles.

correction u_1
correction u_2
correction u_3
je programme ma TI 83 Premium CE

b. Recopier le script python ci-dessous et compléter les lignes 3 et 6 pour que liste(k)
prenne en paramètre un entier naturel k et renvoie la liste des premières valeurs
de la suite (u_n) de u_0 à u_k.

correction

2. On admet que, pour tout entier naturel n, u_n est strictement positif.
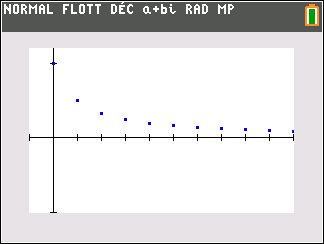
Déterminer le sens de variation de la suite (u_n).

correction n°1
correction n°2
je valide avec ma TI 83 Premium CE

3. En déduire que la suite (u_n) converge.

correction

4. Déterminer la valeur de sa limite.

correction
je valide avec ma TI 83 Premium CE

5. a. Conjecturer une expression de u_n en fonction de n.

correction

5. b. Démontrer par récurrence la conjecture précédente

correction

©2020 – Math’O karé SAS

(u_n) est une suite définie par récurrence.

Lorsqu’on veut calculer, par exemple  u_1, il faut remplacer tous les n par l’entier précédent, ici  0 dans la formule u_{n+1}=\frac{u_n}{1+u_n}.

u_{0+1}=\frac{u_0}{1+u_0}

On remplace u_0 par sa valeur 1. 

u_{1}=\frac{1}{1+1}\\u_{1}=\frac{1}{2}

(u_n) est une suite définie par récurrence.

Lorsqu’on veut calculer, par exemple  u_2, il faut remplacer tous les n par l’entier précédent, ici  1 dans la formule u_{n+1}=\frac{u_n}{1+u_n}.

u_{1+1}=\frac{u_1}{1+u_1}

On remplace u_1 par sa valeur \frac{1}{2}. 

u_{2}=\frac{\frac{1}{2}}{\frac{1}{2}+1}\\u_{2}=\frac{\frac{1}{2}}{\frac{3}{2}}\\u_{2}=\frac{1}{2}\times \frac{2}{3}\\u_{2}=\frac{1}{3}

(u_n) est une suite définie par récurrence.

Lorsqu’on veut calculer, par exemple  u_3, il faut remplacer tous les n par l’entier précédent, ici  2 dans la formule u_{n+1}=\frac{u_n}{1+u_n}.

u_{2+1}=\frac{u_2}{1+u_2}

On remplace u_2 par sa valeur \frac{1}{3}. 

u_{3}=\frac{\frac{1}{3}}{\frac{1}{3}+1}\\u_{3}=\frac{\frac{1}{3}}{\frac{4}{3}}\\u_{3}=\frac{1}{3}\times \frac{3}{4}\\u_{3}=\frac{1}{4}

Au clavier

A l’écran

Taper sur la touche mode et sélectionner SUITE sur la 5ème ligne. Puis quitter avec 2nde mode

Taper ensuite sur la touche f(x) en haut à gauche. Comme la suite  est définie par récurrence, à l’aide des flèches, dans TYPE sélectionner SUITE(n+1).

On programme la suite.

Pour cela sur la ligne nMin saisir  le plus petit rang, c’est souvent 0 mais il arrive que ce soit 1 ou autre chose. 

Puis compléter la ligne u(n+1)=. Pour saisir n taper au clavier sur la touche X,T,O,n et pour saisir u taper sur la touche 2nde puis sur la touche 7.

Compléter la ligne u(0)=

Pour afficher les termes de la suite, s’assurer que le tableur est bien paramétré, faire 2nde puis fenêtre on doit avoir 0, 1, AUTO et AUTO.

Taper sur la touche 2nde et sur la touche graphe, le tableur apparaît.

On complète les lignes 3 et 6.
Sur la ligne 3, on affecte à u la valeur initiale u_0 c’est-à-dire 1. 
Sur la ligne 5, on affecte à u le terme suivant de la suite \frac{u}{u+1}.

On admet que, pour tout entier naturel n, u_n est strictement positif.
Déterminer le sens de variation de la suite (u_n).

On peut comparer \frac{u_{n+1}}{u_n} et 1 puisque les termes de la suite (u_n) sont strictement positifs

On calcule \frac{u_{n+1}}{u_n} en remplaçant u_{n+1} par \frac{u_{n}}{ 1+u_n}

\frac{u_{n+1}}{u_n}=\frac{\frac{u_{n}}{1+u_n}}{u_n}

\frac{u_{n+1}}{u_n}=\frac{u_{n}}{1+u_n}\times \frac{1}{u_n}

\frac{u_{n+1}}{u_n}=\frac{1}{1+u_n}

Comme u_{n}>0 , u_{n}+1>1 et \frac{1}{1+u_n} <1 .

Donc \frac{u_{n+1}}{u_n}<1 donc la suite (u_n) est décroissante sur \mathbf{N}

On admet que, pour tout entier naturel n, u_n est strictement positif.
Déterminer le sens de variation de la suite (u_n).

On peut étudier le signe de  u_{n+1}-u_n.

On calcule u_{n+1}-u_n en remplaçant u_{n+1} par \frac{u_{n}}{ 1+u_n}

u_{n+1}-u_n=\frac{u_{n}}{1+u_n}-u_n

u_{n+1}-u_n=\frac{u_{n}}{1+u_n}-u_n\times \frac{(1+u_{n})}{1+u_n}

u_{n+1}-u_n=\frac{u_n-u_n-u_n^2}{1+u_n}

u_{n+1}-u_n=\frac{-u_n^2}{1+u_n}

Comme u_{n}>0 , u_{n}+1>1 donc u_{n}+1 est positif.

-u_{n}^2 est négatif.

Donc \frac{-u_n^2}{1+u_n} est négatif.

Donc u_{n+1}-u_n est négatif.

Donc la suite (u_n) est décroissante sur \mathbf{N}

En examinant nuage de points et tableur, on constate que la suite (u_n) est bien décroissante.

Remarque pour obtenir les valeurs décimales dans le tableur, appuyer sur la touche mode et sélectionner DEC sur la onzième ligne RESULTAT .

On veut en déduire que la suite (u_n) converge.

Comme (u_n) est décroissante et minorée par 0, alors la suite (u_n) converge vers une limite finie.

On veut déterminer la limite l de la suite (u_n).

Comme la fonction définie par f(x)=\frac{x}{x+1} est continue sur [0;+\infty[, la limite l vérifie f(l)=l.

On résout f(l)=l.

\frac{l}{l+1}=l

On fait le produit en croix.

l^2+l=l\\l^2=0\\l=0

Donc la limite de la suite (u_n) vaut 0.

En examinant nuage de points et tableur, on constate que la limite de la suite (u_n) semble être égale à 0.

Compte-tenu de ce qu’on observe dans le tableau ci-dessous, il paraît raisonnable de conjecturer que u_n=\frac{1}{n+1} pour n\in \mathbf{N}.

On considère la suite (u_n) définie par u_0=1 et u_{n+1}=\frac{u_n}{1+u_n}.

Montrer par récurrence que  u_n=\frac{1}{n+1} pour n \in \mathbf{N}.

Initialisation : J’écris la propriété au premier rang en remplaçant tous les n par 0.

u_{0}=\frac{1}{0+1}=1 vraie car u_0=1

Transmission ou hérédité : 

On suppose que u_n=\frac{1}{n+1}.

Montrons que u_{n+1}=\frac{1}{(n+1)+1}

u_{n+1}=\frac{u_n}{1+u_n}\\\hspace{0.8cm}=\frac{\frac{1}{n+1}}{1+\frac{1}{n+1}}\\\hspace{0.8cm}=\frac{\frac{1}{n+1}}{\frac{n+1}{n+1}+\frac{1}{n+1}}\\\hspace{0.8cm}=\frac{\frac{1}{n+1}}{\frac{(n+1)+1}{n+1}}\\\hspace{0.8cm}=\frac{1}{n+1}\times{\frac {n+1}{(n+1)+1}}\\\hspace{0.8cm}=\frac{1}{(n+1)+1}

étape n°1 : j’exprime u_{n+1} en fonction de u_{n}.

étape n°2 : Je remplace u_n par  \frac{1}{n+1}.

étape n°3 : je mets le dénominateur au même dénominateur. 

 

étape n°4 : j’ajoute en bas.

étape n°5 : diviser revient à multiplier par l’inverse.

étape n°6 : on simplifie par n+1.

On a bien montré que u_{n+1}=\frac{1}{(n+1)+1}

Conclusion : J’écris la propriété au rang  n et je rajoute pour tout n.

u_n=\frac{1}{n+1} pour n \in \mathbf{N}.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.