Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des
quatre réponses proposées est exacte. Les six questions sont indépendantes.
Une réponse incorrecte, une réponse multiple ou l’absence de réponse à une question ne rapporte ni
n’enlève de point. Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse
choisie.
Aucune justification n’est demandée.
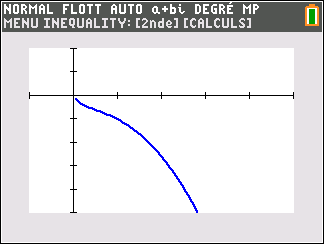
1. On considère la fonction f définie pour tout réel x par f(x)=ln(1+x^2).
Sur \mathbf{R}, l’équation f(x)=2022
a. n’admet aucune solution.
b. admet exactement une solution.
c. admet exactement deux solutions.
d. admet une infinité de solutions
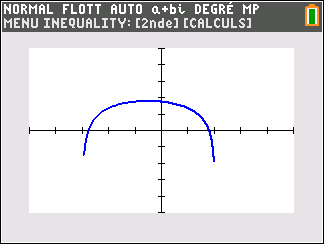
2. On considère la fonction g définie pour tout réel x positif par g(x)=xln(x)-x^2.
On note C_g sa courbe représentative dans un repère du plan.
a. La fonction g est convexe sur ]0;+\infty[.
b. La fonction g est concave sur ]0;+\infty[.
c. La courbe C_g admet exactement un point d’inflexion sur ]0;+\infty[.
d. La courbe C_g admet exactement deux points d’inflexion sur ]0;+\infty[.
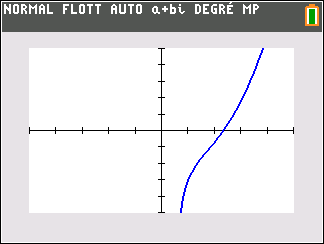
3. On considère la fonction f définie sur ]-1;1[ par f(x)=\frac{x}{1-x^2}.
Une primitive de la fonction f est la fonction g définie sur l’intervalle ]-1;1[ par :
a. g(x)=-\frac{1}{2}ln(1-x^2).
b. g(x)=\frac{1+x^2}{(1-x^2)^2}.
c. g(x)=\frac{x^2}{2(x-\frac{x^3}{3})}.
d. g(x)=\frac{x^2}{2}ln(1-x^2).
4. La fonction x\to ln(-x^2-x+6) est définie sur
a. ]-3;2[.
b. ]-\infty;6[.
c. ]0;+\infty[.
d. ]2;+\infty[.
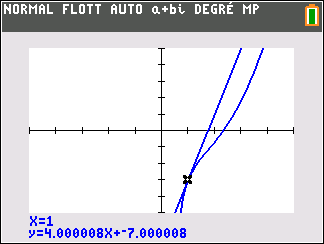
5. On considère la fonction f définie sur ]0;5[ par
f(x)=x^2-4x+3 ln(2x-1)
Une équation de la tangente à la courbe représentative de f au point d’abscisse 1 est :
a. y=4x-7.
b. y=2x-4.
c. y=-3(x-1)+4.
d. y=2x-1.
6. L’ensemble S des solutions dans \mathbf{R} de l’inéquation ln(x+3)<2ln(x+1) est :
a. S=]-\infty;-2[\cup]1;+\infty[.
b. S=]1;+\infty[.
c. S=\emptyset.
d. S=]-1;1[.