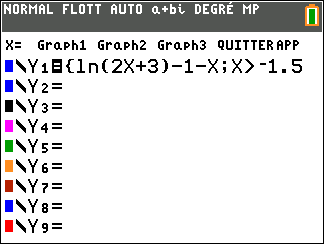
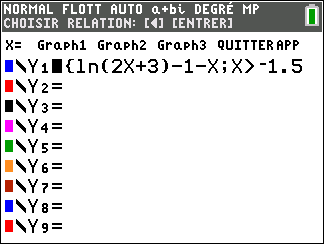
On considère la fonction f définie sur ]-1.5;+\infty[ par f(x)=ln(2x+3)-1.
Le but de cet exercice est d’étudier la convergence de la suite (u_n) définie par :
u_0=0 et u_{n+1}=f(u_n) pour tout entier naturel n.
Partie A : Étude d’une fonction auxiliaire
On considère la fonction g définie sur ]-1.5;+\infty[ par g(x)=f(x)-x
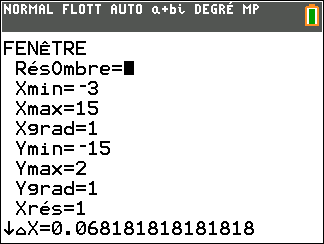
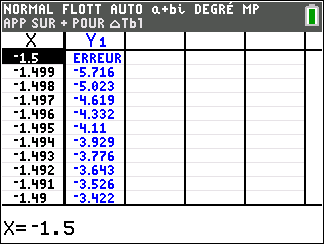
1. Déterminer la limite de la fonction g en -1.5.
On admet que la limite de la fonction g en +\infty est -\infty.
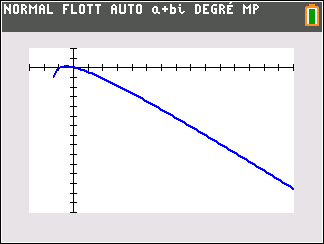
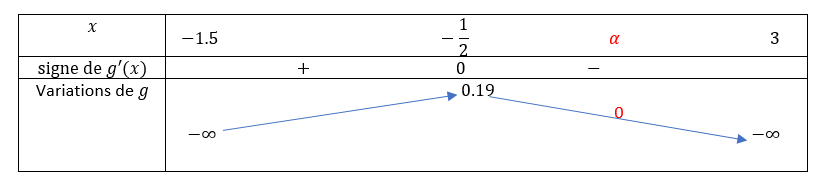
2. Étudier les variations de la fonction g sur ]-1.5;+\infty[.
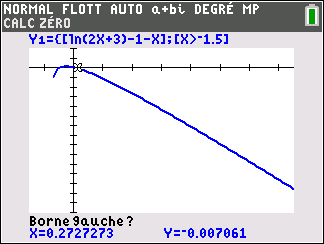
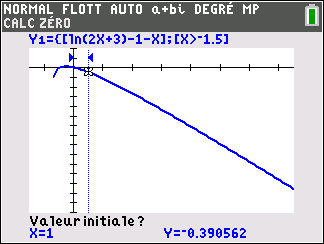
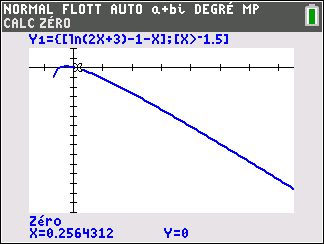
3. a. Démontrer que, dans l’intervalle ]-1.5;+\infty[, l’équation g(x)=0 admet une unique solution \alpha.
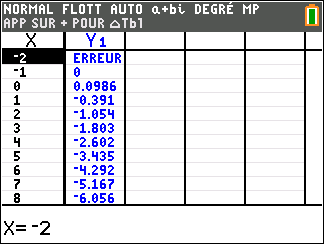
b. Déterminer un encadrement de \alpha d’amplitude 10^{-2}.
Partie B : Étude de la suite (u_n)
On admet que la fonction f est strictement croissante sur ]-1.5;+\infty[.
1. Soit x un nombre réel. Montrer que si x\in\left[-1;\alpha\right] alors f(x)\in]-1;\alpha].
2. a. Démontrer par récurrence que pour tout entier naturel n :
-1\leq u_n\leq u_{n+1}\leq \alpha.
b. En déduire que la suite (u_n) converge.