Sommaire
Expérience aléatoire
Une expérience aléatoire est une expérience dont le résultat dépend du hasard.
L’ensemble de tous les résultats possibles d’une expérience aléatoire s’appelle l’univers de l’expérience.
On le note en général \Omega.
Exemple 1 :
Je jette un dé à 6 faces.
Déterminer l’univers de l’expérience.
Exemple 2 :
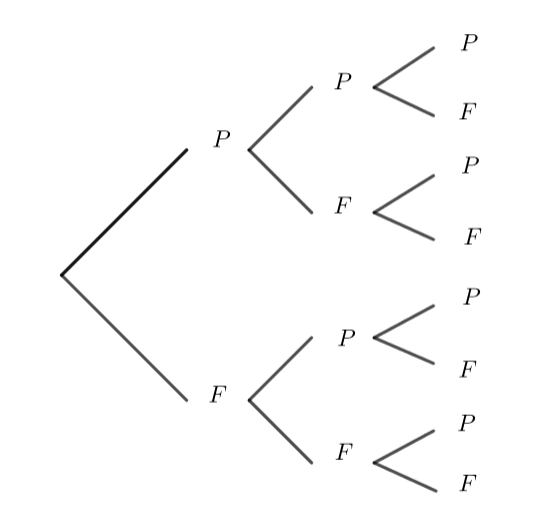
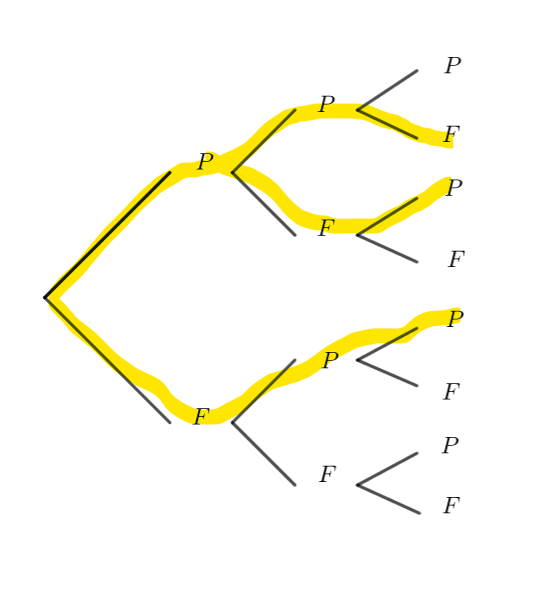
je jette une pièce de monnaie trois fois de suite.
Déterminer l’univers de l’expérience.
Exemple n°3 :
je tire une carte dans un jeu de 32 cartes.
Déterminer l’univers de l’expérience.
Evènements
Définition 2:
Soit une expérience aléatoire d’univers \Omega.
Chacun des résultats possibles s’appelle une éventualité (ou un événement élémentaire ou une issue).
On appelle événement tout sous ensemble de \Omega.
Un événement est donc constitué de zéro, une ou plusieurs éventualités.
Exemple 1 :
Je jette un dé à 6 faces.
Déterminer toutes les isues qui se trouvent dans l’évènement A : le résultat obtenu est un multiple de 3 et dans l’évènement B : le résultat est supérieur ou égal à 2.
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
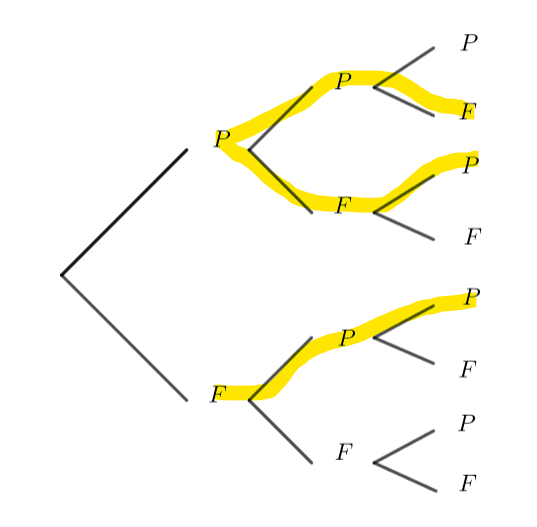
Déterminer toutes les isues qui se trouvent dans l’évènement A : le résultat obtenu comporte exactement une fois face et dans l’évènement B : le résultat comporte plus de pile que de face.
Exemple n°3 :
Je tire une carte dans un jeu de 32 cartes.
Déterminer toutes les issues qui se trouvent dans l’évènement A : le résultat obtenu est un cœur et dans l’évènement B : le résultat est une figure rouge..
Définition 3
- l’événement impossible est la partie vide, noté \emptyset lorsque aucune issue ne le réalise.
- l’événement certain est \Omega, lorsque toutes les issues le réalisent.
- l’événement contraire de A noté \overline{A} est l’ensemble des éventualités de \Omega qui n’appartiennent pas à A.
- l’événement A\cup B (lire « A union B » ou « A ou B») est constitué des éventualités qui appartiennent soit à A, soit à B, soit aux deux ensembles.
- l’événement A\cap B (lire « A inter B » ou « A et B») est constitué des éventualités qui appartiennent à la fois à A et à B.
Exemple 1 :
Je jette un dé à 6 faces.
Déterminer toutes les issues (quand c’est possible, sinon faire une phrase) qui se trouvent dans les évènements
A\cup B ; A\cap B ; \overline A et \overline B
Où A et B sont les évènements définis précédemment.
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
Déterminer toutes les issues (quand c’est possible, sinon faire une phrase)qui se trouvent dans les évènements
A\cup B ; A\cap B ; \overline A et \overline B
Où A et B sont les évènements définis précédemment.
Exemple 3 :
Je tire une carte dans un jeu de 32 cartes.
Déterminer toutes les issues (quand c’est possible, sinon faire une phrase)qui se trouvent dans les évènements
A\cup B ; A\cap B ; \overline A et \overline B
Où A et B sont les évènements définis précédemment.
Définition 4:
On dit que A et B sont incompatibles si et seulement si A\cap B=\emptyset
Deux événements sont incompatibles lorsqu’ils ne contiennent aucune issue commune.
Exemple 1 :
Je jette un dé à 6 faces
Trouver deux évènements A et B incompatibles.
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
Trouver deux évènements A et B incompatibles.
Exemple 3 :
Je tire une carte dans un jeu de 32 cartes.
Trouver deux évènements A et B incompatibles.
Probabilités
Définition 5:
La probabilité d’un événement élémentaire est un nombre réel tel que:
Ce nombre est compris entre 0 et 1
La somme des probabilités de tous les événements élémentaires de l’univers vaut 1
Propriétés :
p(\emptyset)=0\\p(\Omega)=1\\p(\overline A)=1-p(A)Exemple 1 :
Je jette un dé à 6 faces.
Calculer p(1)=\\\hspace{1.1cm}p(2)=
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
Calculer p(PPP)=\\\hspace{1.1cm}p(PPF)=
Exemple 3 :
Je tire une carte dans un jeu de 32 cartes.
Calculer p(roi\heartsuit)=\\\hspace{1.1cm}p(7\clubsuit)=
Propriété : la probabilité d’un évènement est la somme des probabilités des évènements élémentaires qui le constituent.
Exemple 1 :
Je jette un dé à 6 faces.
Calculer les probabilités de l’évènement A : le résultat obtenu est un multiple de 3 et de l’évènement B : le résultat est supérieur ou égal à 2.
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
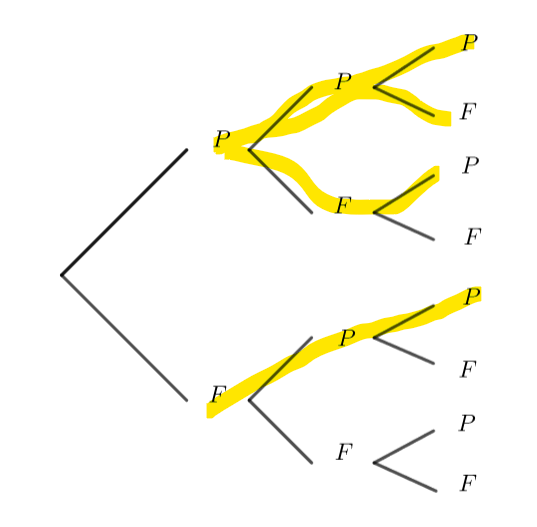
Calculer les probabilités de l’évènement A : le résultat obtenu comporte exactement une fois face et de l’évènement B : le résultat comporte plus de pile que de face .
Exemple 3 :
Je tire une carte dans un jeu de 32 cartes.
Calculer les probabilités de l’évènement A : le résultat obtenu est un cœur et de l’évènement B : le résultat est une figure rouge.
Théorème :
Quels que soient les événements A ; B et \Omega
p(A\cup B)=p(A)+p(B)-p(A\cap B)
En particulier, si A et B sont incompatibles :
p(A\cup B)=p(A)+p(B)
Exemple 1 :
Je jette un dé à 6 faces.
En utilisant les résultats précédents, calculer la probabilité de l’évènement le résultat obtenu est un multiple de 3 et un nombre supérieur ou égal à 2.
En déduire la probabilité de l’évènement le résultat obtenu est un multiple de 3 ou un nombre supérieur ou égal à 2.
Exemple 2 :
Je jette une pièce de monnaie trois fois de suite.
En utilisant les résultats précédents, calculer la probabilité de l’évènement le résultat obtenu comporte exactement une fois face et plus de pile que de face.
En déduire la probabilité de l’évènement le résultat obtenu comporte exactement une fois face ou plus de pile que de face.
Exemple n°3 :
Je tire une carte dans un jeu de 32 cartes.
En utilisant les résultats précédents, calculer la probabilité de l’évènement le résultat obtenu est un coeur et une figure rouge.
En déduire la probabilité de l’évènement le résultat obtenu est un coeur ou une figure rouge.
Définition 5:
Lorsque chaque évènement élémentaire a la même probabilité de se produire, on dit qu’il y a équiprobabilité.
C’est le cas pour les trois exemples du cours.
Propriété:
On suppose que l’univers est composé de n événements élémentaires
Dans le cas d’équiprobabilité, chaque événement élémentaire a pour probabilité :\frac{1}{n}
Si un événement A de Ω est composé de m événements élémentaires, alors p(A)=\frac{m}{n}
Exemple 1 :
je jette un dé à 6 faces
Calculer les probabilités de l’évènement C : le résultat obtenu est un diviseur de 6 et de l’évènement D : le résultat est inférieur ou égal à 3.
Exemple 2 :
je jette une pièce de monnaie trois fois de suite
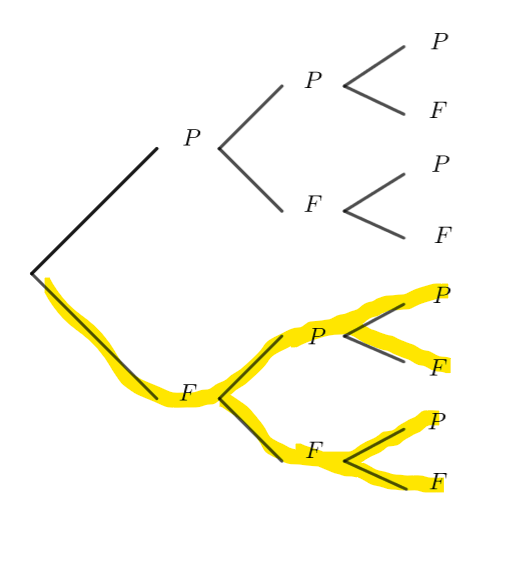
Calculer les probabilités de l’évènement C : le résultat obtenu commence par face et de l’évènement D : le résultat exactement deux piles.
Exemple n°3 :
je tire une carte dans un jeu de 32 cartes
Calculer les probabilités de l’évènement C : le résultat obtenu est un roi et de l’évènement D : le résultat est un pique.