Sommaire
Ensemble de définition des fonctions de référence
Cas des fonctions affines
Par exemple f(x)=2x-4
Représentation graphique
Représentation tableur
Représentation algébrique
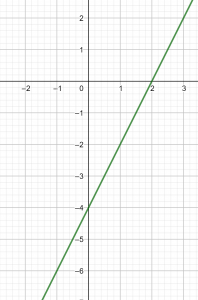
Il semble qu’on peut toujours déterminer graphiquement l’image d’un nombre à l’aide de la courbe ci-dessus.
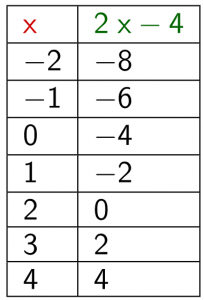
Il semble qu’il n’y aura jamais de message d’erreur dans la deuxième colonne.
f(x)=2x-4
Pour calculer l’image d’un nombre a, je remplace tous les x par ce nombre a dans f(x)=2x-4 et je calcule en respectant la priorité des opérations.
Ici on multiplie par 2 puis on ajoute -4.
Quelque soit le nombre réel x, le calcul est toujours possible.
La fonctionf est définie sur R.
la fonction carré
représentation graphique
représentation tableur
représentation algébrique
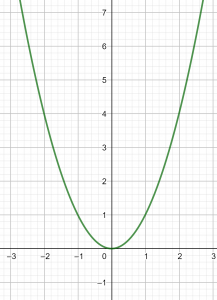
Il semble que pour tout nombre réel x, on peut construire son image par la courbe ci-dessus
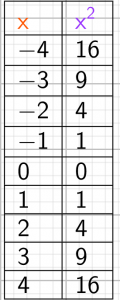
Il semble qu’il n’y aura jamais de message d’erreur dans la deuxième colonne.
f(x)=x^{2}
Pour calculer l’image d’un nombre a , je remplace tous les x par a dans
f(x)=x^{2}
Quelque soit le nombre réel x , le calcul est toujours possible.
La fonction carré est définie sur R.
la fonction cube
représentation graphique
représentation tableur
représentation algébrique
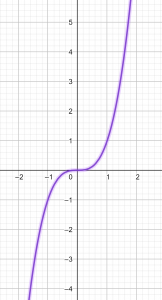
Il semble que pour tout nombre réel x, on peut construire son image par la courbe ci-dessus
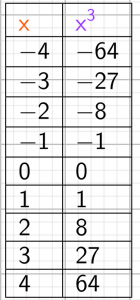
Il semble qu’il n’y aura jamais de message d’erreur dans la deuxième colonne.
f(x)=x^{3}
Pour calculer l’image d’un nombre a , je remplace tous les x par a dans
f(x)=x^{3}
Quelque soit le nombre réel x , le calcul est toujours possible.
La fonction cube est définie sur R.
la fonction inverse
représentation graphique
représentation tableur
représentation algébrique
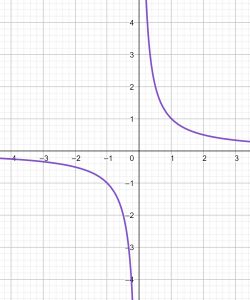
Il semble que pour tout nombre réel x non nul, on peut construire son image par la courbe ci-dessus.
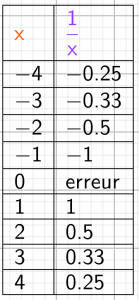
Il y a un message d’erreur pour x=0.
f(x)=\frac{1}{x}
Pour calculer l’image d’un nombre a je remplace tous les x par a dans
f(x)=\frac{1}{x}Quelque soit le nombre réel non nul x , le calcul est toujours possible.
En revanche on ne peut pas calculer l’image de 0
La fonction inverse est définie sur l’ensemble des réels non nuls noté R^{*}. On peut aussi utiliser la notation intervalle : ]-\infty;0[\cup]0;+\infty[.
fonction racine carrée
représentation graphique
représentation tableur
représentation algébrique
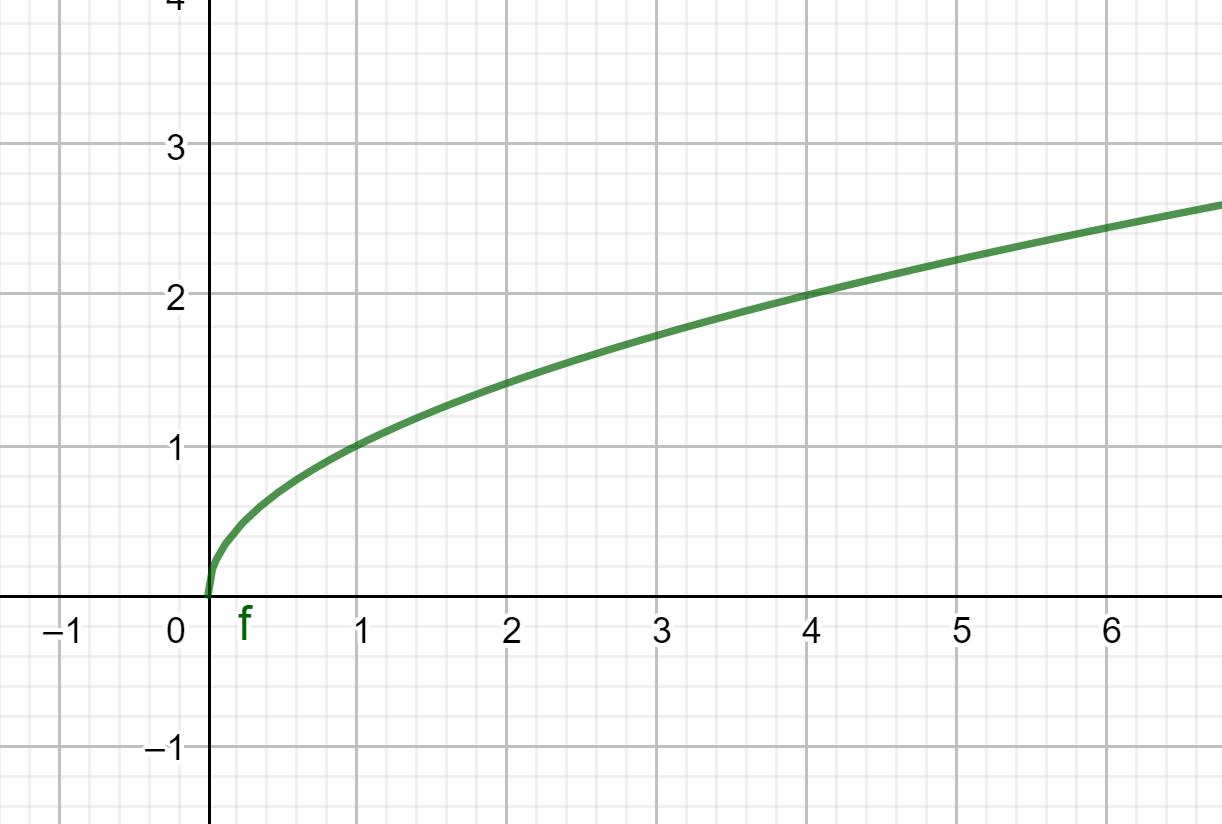
Il semble qu’on ne peut construire que les images des nombres positifs par la courbe ci-dessous.
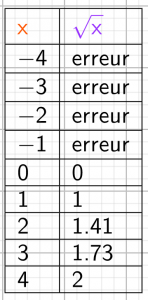
Il semble que les nombres négatifs n’ont pas d’image.
f(x)=\sqrt{x}
Pour calculer l’image d’un nombre a , je remplace tous les x par a dans
f(x)=\sqrt{x}Le calcul n’est possible que pour les nombres réels x positifs.
La fonction racine carrée est définie sur [0;+\infty[.
Ensemble de définition d’une fonction
On convient que l’ensemble de définition d’une fonction f est l’ensemble des nombres réels x pour lesquels on peut calculer f(x) .
Remarque: en classe de seconde, l’ensemble sur lequel est définie la fonction f est généralement donné dans l’énoncé.
Calculer l’image d’un nombre
METHODE: Pour calculer l’image d’un nombre a , je remplace tous les x par a dans f(x)=…. Puis j’effectue la séquence de calculs en respectant la priorité des opérations.
Exercice n°1
soit f(x)=2(x-1)^{2}+3 définie sur R.
Calculer f(1) , f(0) ,f(-1) etf(\frac{1}{3})
Exercice n°2
soit f(x)=3x-2 définie sur R.
Calculer f(\frac{1}{3}) , f(0) et f(-2)
Exercice n°3
soit f(x)=(x-4)(3x-5) définie sur R.
Calculer f(4) , f(\frac{1}{7}) et f(-2)
Exercice n°4
soit f(x)=\frac{x-3}{2x-4} définie sur R privé de 2.
Calculer f(3) , f(\frac{1}{2}) et f(0)
Exercice n°5
soit f(x)=x^{2}+2x+1 définie sur R .
Calculer f(0) , f(\frac{1}{2}) , f(\sqrt{3}) et f(-1)
Exercice n°6
soit f(x)=2\sqrt{x-3}+6 définie sur [3;+\infty[
Calculer f(3) , f(5) et f(7)
Exercice n°7 : soit f(x)=(x-2)^{2}-9 définie sur R.
- Déterminer la forme développée et réduite de f(x)
2. Déterminer la forme factorisée de f(x)
3. En utilisant l’une des trois formes suivantes:
(e) f(x)=(x-2)^{2}-9
(d) f(x)=x^{2}-4x-5
(f) f(x)=(x-5)(x+1)
Calculer les images suivantes : f(0), f(5), f(2), f(\sqrt{5})










