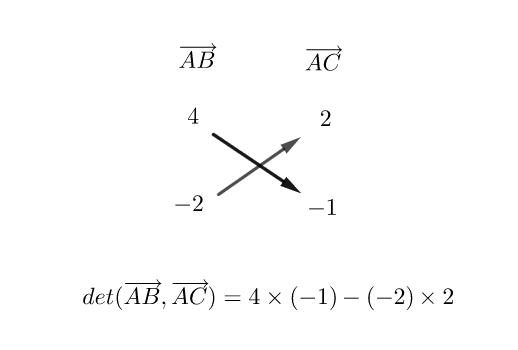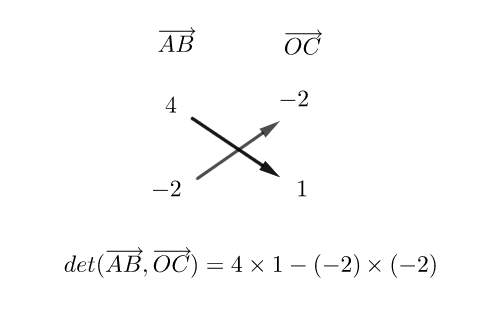Sommaire
Activité d’approche
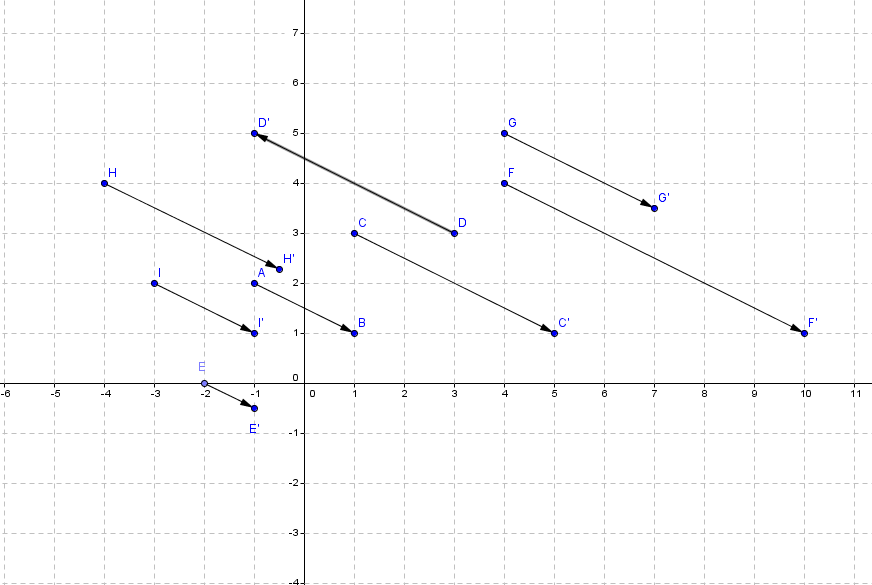
On a placé des points et un vecteur dans un repère.
- Placer C’ tel que \overrightarrow{CC’ }= 2 \overrightarrow{AB }.
Les vecteurs \overrightarrow{CC’ } et 2 \overrightarrow{AB } ont même direction. Pour cela avec Géogébra, tracer une droite parallèle à (AB) passant par C.
Cliquer sur le quatrième onglet à partir de la gauche en haut et sélectionner Parallèle dans le menu déroulant. Puis cliquer sur la droite (AB) et sur le point C.
La longueur ( ou norme) du vecteurs \overrightarrow{CC’ } est 2 fois celle du vecteur \overrightarrow{AB } . Avec Géogébra, tracer le cercle de centre C et de rayon 2AB.
Cliquer sur le sixième onglet à partir de la gauche en haut et sélectionner Cercle (centre-rayon) dans le menu déroulant. Puis cliquer sur le point C et dans la case Rayon écrire 2AB.
Remarque : la droite et le cercle ont deux points communs.
Les vecteurs \overrightarrow{CC’ } et 2 \overrightarrow{AB } ont même sens car le vecteur \overrightarrow{AB } est multiplié par 2 qui est un nombre positif. Donc parmi les deux points d’intersection obtenus précédemment , on ne garde que celui où on va de C vers C’ comme on va de A vers B.
On l’appelle C’.
Avec Géogébra, cliquer sur le deuxième onglet à partir de la gauche en haut et sélectionner Point dans le menu déroulant. Puis cliquer sur le point d’intersection que l’on a choisi. Eventuellement le renommer en C’ en cliquant gauche sur C’ et en sélectionnant Renommer dans le menu déroulant.
On trace le vecteur \overrightarrow{CC’ }.
Pour cela avec Géogébra, cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur les points C et C’ dans cet ordre.
2. Placer D’ tel que \overrightarrow{DD’ }= -2 \overrightarrow{AB }.
3. Placer E’ tel que \overrightarrow{EE’ }= \frac{1}{2} \overrightarrow{AB }.
4. Placer F’ tel que \overrightarrow{FF’ }= 3 \overrightarrow{AB }.
5. Placer G’ tel que \overrightarrow{GG’ }= \frac{3}{2} \overrightarrow{AB }.
6. Placer H’ tel que \overrightarrow{HH’ }= \frac{7}{4} \overrightarrow{AB }.
7. Placer I’ tel que \overrightarrow{II’ }= \overrightarrow{AB }.
2. Synthèse : donner une définition du vecteur k\vec{u} ( k fois le vecteur \vec{u} ) en fonction du vecteur \vec{u} .
Déterminant de deux vecteurs
Définition
On considère deux vecteurs \vec{u}(x;y) et \vec{v}(x’;y’) .
Le déterminant de \vec{u} et \vec{v} noté det(\vec{u}; \vec{v}) est le nombre
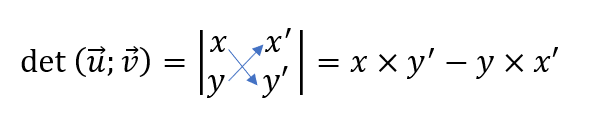
Exemple :
On considère deux vecteurs \vec{u}(3;-2) et \vec{v}(1;1) .
On calcule le déterminant ainsi :
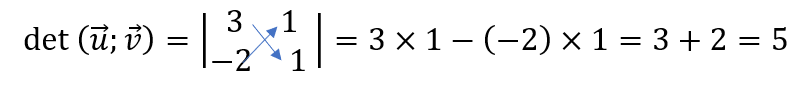
vecteurs colinéaires
Définition
deux vecteurs \vec{u} et \vec{v} sont colinéaires s’il existe un réel k tel que\vec{u} =k\vec{v}.
Critère de colinéarité
Deux vecteurs \vec{u}(x;y) et \vec{v}(x’;y’) sont colinéaires si et seulement si le déterminant de \vec{u} et \vec{v} est nul c’est-à-dire det(\vec{u}; \vec{v})=0
propriétés
k(\vec{u}+\vec{v})=k\vec{u}+k\vec{v}\\(k+k’)\vec{u})=k\vec{u}+k’\vec{u}\\(kk’)\vec{u}=k(k’\vec{u})Exercice n°1
Soient A(-1;1) et B(3;2). On note I le milieu de [AB]
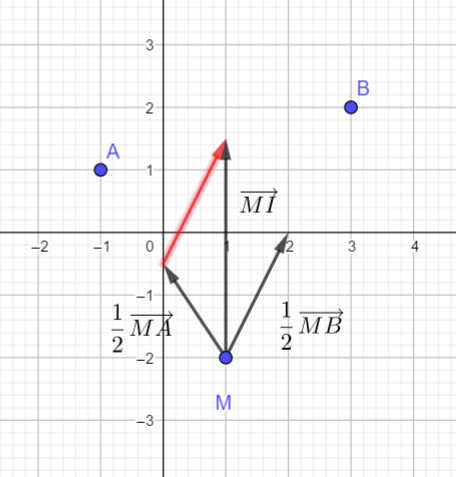
Partie A : Dans cette partie, M(1;-2)
- Déterminer par le calcul les coordonnées de I .
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le deuxième onglet à partir de la gauche en haut et sélectionner Milieu ou centre dans le menu déroulant. Puis cliquer sur le point A et sur le point B. Géogébra le nomme C , on peut le renommer en I en cliquant gauche sur le et en sélectionnant Renommer dans le menu déroulant.
2. a. Déterminer les coordonnées du vecteur \overrightarrow{MA }, puis celles du vecteur \frac{1}{2}\overrightarrow{MA }.
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur le point M et sur le point A. Dans la colonne Algèbre à gauche les coordonnées du vecteur \overrightarrow{MA } apparaissent.
2. b. Déterminer les coordonnées du vecteur \overrightarrow{MB }, puis celles du vecteur \frac{1}{2}\overrightarrow{MB }.
2.c. En déduire les coordonnées du vecteur \frac{1}{2}\overrightarrow{MA }+\frac{1}{2}\overrightarrow{MB }.
3. Calculer les coordonnées du vecteur \overrightarrow{MI }. Que constatez-vous ?
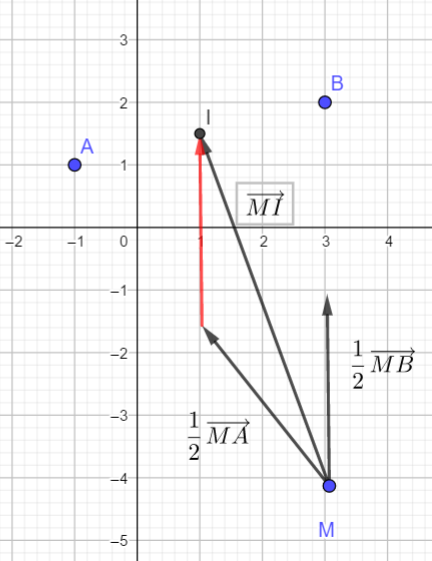
Partie B : Dans cette partie, M(a;b)
1. a. Déterminer les coordonnées du vecteur \overrightarrow{MA }, puis celles du vecteur \frac{1}{2}\overrightarrow{MA }.
1. b. Déterminer les coordonnées du vecteur \overrightarrow{MB }, puis celles du vecteur \frac{1}{2}\overrightarrow{MB }.
1.c. En déduire les coordonnées du vecteur \frac{1}{2}\overrightarrow{MA }+\frac{1}{2}\overrightarrow{MB }.
2. Calculer les coordonnées du vecteur \overrightarrow{MI }. Que constatez-vous ?
Points alignés. Droites parallèles.
Propriété
Langage des points et des droites
A, B , C sont alignés
Langage des vecteurs
\overrightarrow{AB } et \overrightarrow{AC} sont colinéaires.
Langage des coordonnées
les coordonnées de \overrightarrow{AB } et \overrightarrow{AC} sont proportionnelles.
Ou le déterminant de \overrightarrow{AB } et \overrightarrow{AC} est nul
Langage des points et des droites
(AB) et (CD)sont parallèles
Langage des vecteurs
\overrightarrow{AB } et \overrightarrow{CD} sont colinéaires.
Langage des coordonnées
les coordonnées de \overrightarrow{AB } et \overrightarrow{CD} sont proportionnelles.
Ou le déterminant de \overrightarrow{AB } et \overrightarrow{CD} est nul
Exercice n°2
Soient A(-5;0) , B(-1;-2) et C(-3;-1) .
- Calculer les coordonnées du vecteur \overrightarrow{AB } .
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur le point A et sur le point B. Dans la colonne Algèbre à gauche les coordonnées du vecteur \overrightarrow{AB } apparaissent.
2. Calculer les coordonnées du vecteur \overrightarrow{AC } .
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur le point A et sur le point C. Dans la colonne Algèbre à gauche les coordonnées du vecteur \overrightarrow{AC } apparaissent.
3. Calculer le déterminant des vecteurs \overrightarrow{AB } et \overrightarrow{AC } . Que peut-on en déduire ?
Exercice n°3
Soient A(-4;0) , B(0;-2) et C(-2;1) dans un repère (O;\vec{i};\vec{j}).
- Calculer les coordonnées du vecteur \overrightarrow{AB } .
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur le point A et sur le point B. Dans la colonne Algèbre à gauche les coordonnées du vecteur \overrightarrow{AB } apparaissent.
2. Calculer les coordonnées du vecteur \overrightarrow{OC } .
Avant de se lancer dans le calcul, on peut conjecturer le résultat avec Géogébra. Cliquer sur le troisième onglet à partir de la gauche en haut et sélectionner Vecteur dans le menu déroulant. Puis cliquer sur le point O et sur le point C. Dans la colonne Algèbre à gauche les coordonnées du vecteur \overrightarrow{OC} apparaissent.
3. Calculer le déterminant des vecteurs \overrightarrow{AB } et \overrightarrow{OC } . Que peut-on en déduire ?
Exercice n°4
Soient A(1;2) , B(3;3) et C(4;1) dans un repère (O;\vec{i};\vec{j}).
1.a. Déterminer, par le calcul, les coordonnées du point D défini par l’égalité vectorielle suivante \overrightarrow{AD}=-\frac{3}{2}\overrightarrow{AB} .
Avant de se lancer dans les calculs, s’inspirer de la méthode développée dans l’activité d’approche pour placer D dans la fenêtre Géogébra ci-dessus et lire ses coordonnées dans la colonne Algèbre.
1.b. Déterminer, par le calcul, les coordonnées du point E défini par l’égalité vectorielle suivante \overrightarrow{DE}=\frac{3}{2}\overrightarrow{CB} .
Avant de se lancer dans les calculs, s’inspirer de la méthode développée dans l’activité d’approche pour placer E dans la fenêtre Géogébra ci-dessus et lire ses coordonnées dans la colonne Algèbre.
2. Montrer que \overrightarrow{AE}=-\frac{3}{2}\overrightarrow{AC}. Qu’en déduit-on pour les points A,E,C.