Sommaire
Moyenne et écart-type
Définition 1
Pour une série représentée par le tableau d’effectifs ci-dessous :
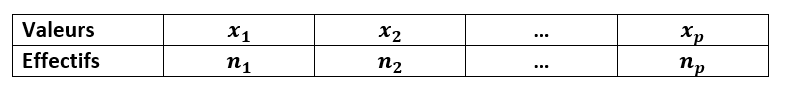
La moyenne pondérée de la série est le nombre noté \overline{x} tel que
\overline{x}=\frac{n_{1}x_{1}+n_{2}x_{2}+…+n_{p}x_{p}}{N}où N représente l’effectif total, c’est-à-dire que
N=n_{1}+n_{2}+…+n_{p}Propriété 1
Si toutes les valeurs d’une série sont multipliées par un nombre, la moyenne est aussi multipliée par ce nombre.
Si on ajoute un même nombre à toutes les valeurs d’une série , la moyenne est aussi augmentée de ce nombre.
Exercice n°1
François a obtenu les notes suivantes au premier trimestre
12 13 11 14 13
Calculer sa moyenne pour le trimestre ( le professeur compte toutes les notes coefficient 1 )
Exercice n°2
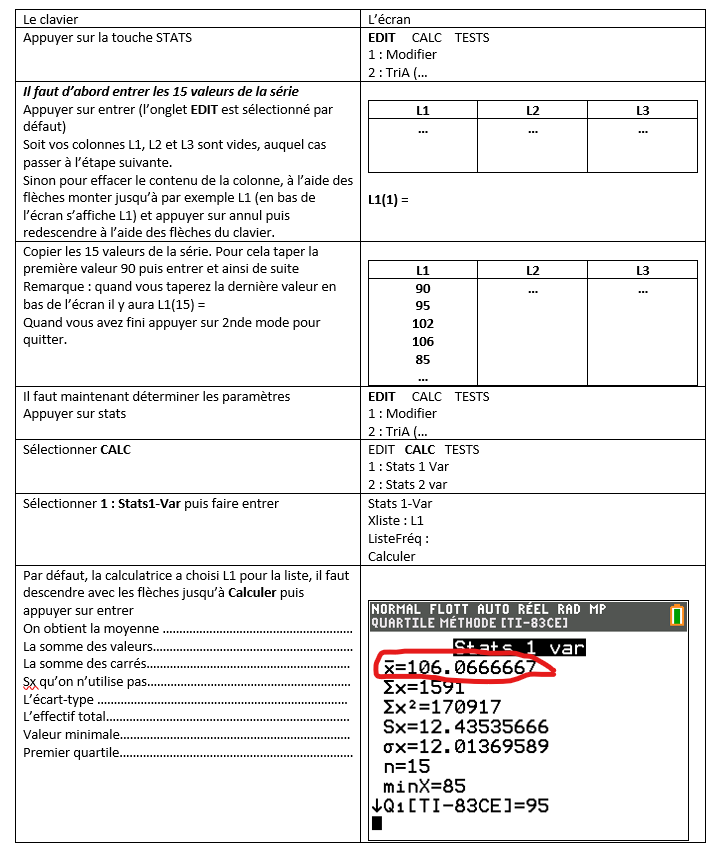
Voici les temps réalisés (en secondes) par 15 élèves de seconde au 500 m.
90 95 102 106 85 120 110 115 116 98 88 111 125 114 116
Calculer le temps moyen pour ce groupe d’élèves.
Exercice n°3
Une opératrice téléphonique a mesuré la durée de communication avec chaque client pendant une journée.

Calculer la durée moyenne d’un appel.
Exercice n°4
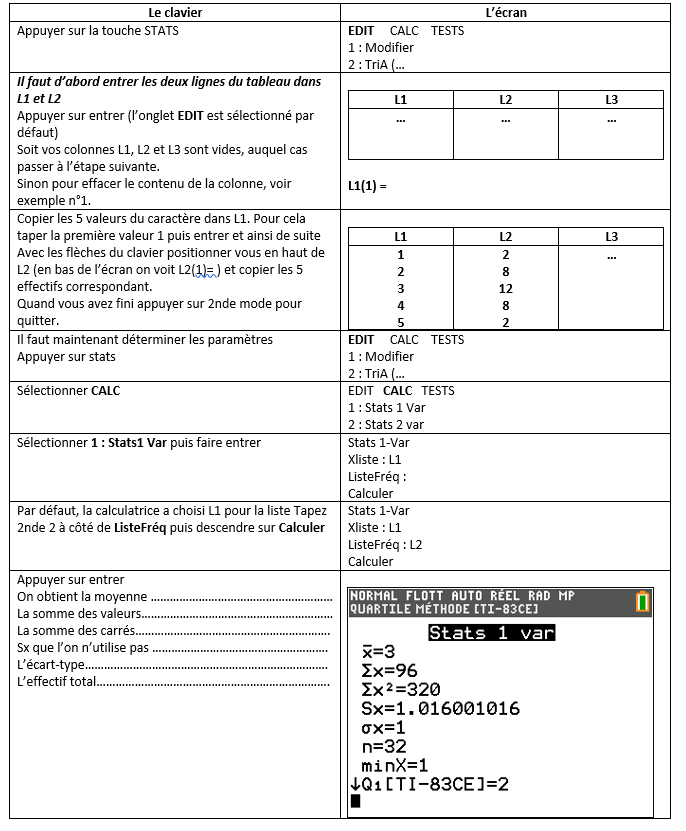
Un professeur de mathématiques demande à ses élèves combien d’enfants comporte leur famille. Il présente les données recueillies dans le tableau ci-dessous :

Calculer le nombre moyen d’enfants par famille.
Exercice n°5
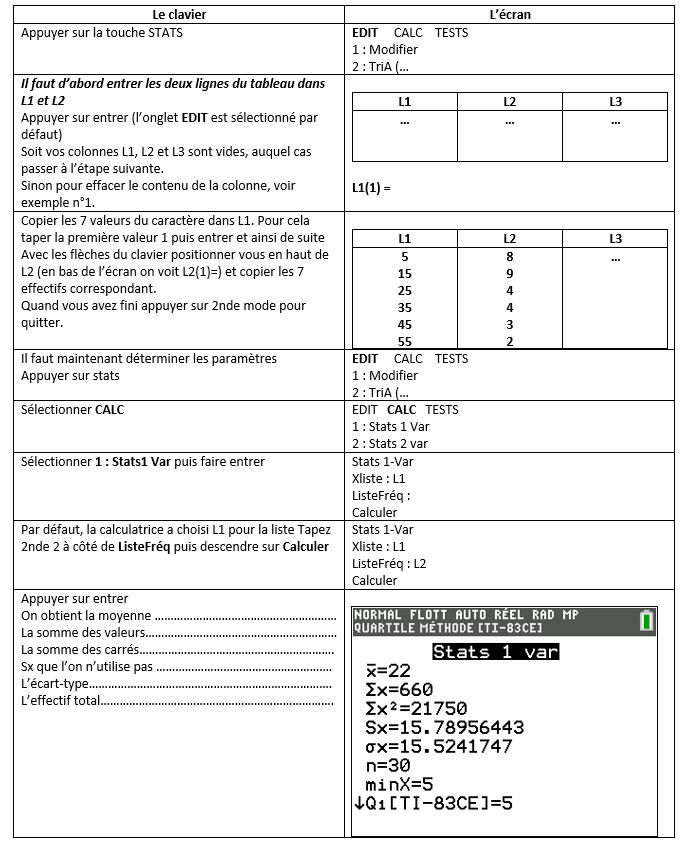
Un professeur de mathématiques demande à ses élèves combien mettent-ils de temps aller/retour pour venir au lycée. Il présente les données recueillies dans le tableau ci-dessous :

Calculer le temps moyen mis par les élèves pour venir au lycée aller/retour .
Définition 2
L’écart-type de la série ci-dessous
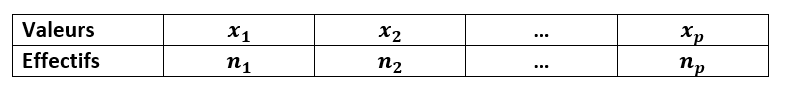
est le nombre positif, noté \sigma, défini par
\sigma=\sqrt{\frac{n_{1}(x_{1}-\overline{x})^{2}+n_{2}(x_{2}-\overline{x})^{2}+…+n_{p}(x_{p}-\overline{x})^{2}}{N}}Exercice n°1bis
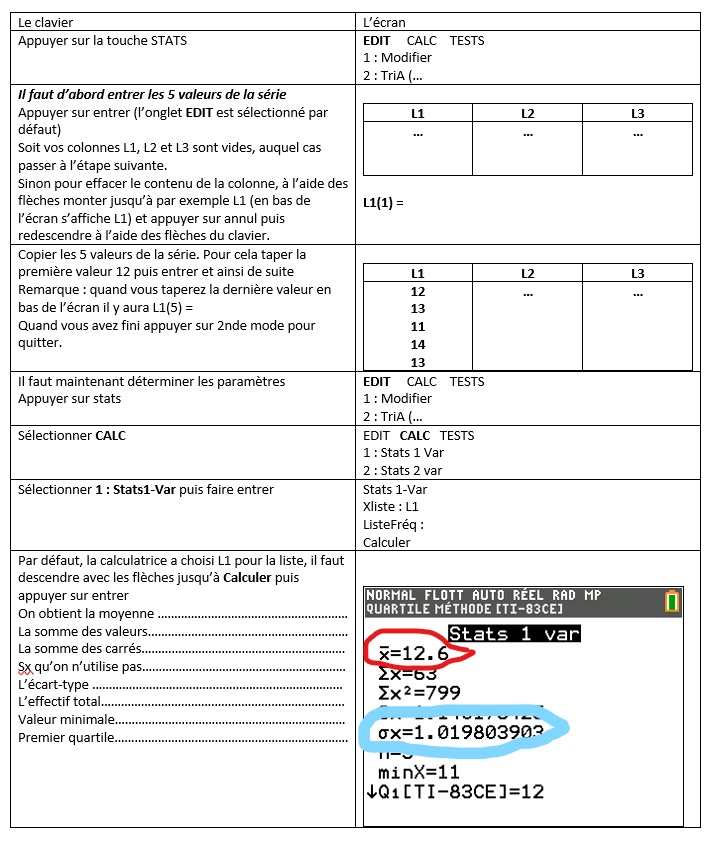
François a obtenu les notes suivantes au premier trimestre
12 13 11 14 13
Calculer sa moyenne pour le trimestre et l’écart-type.
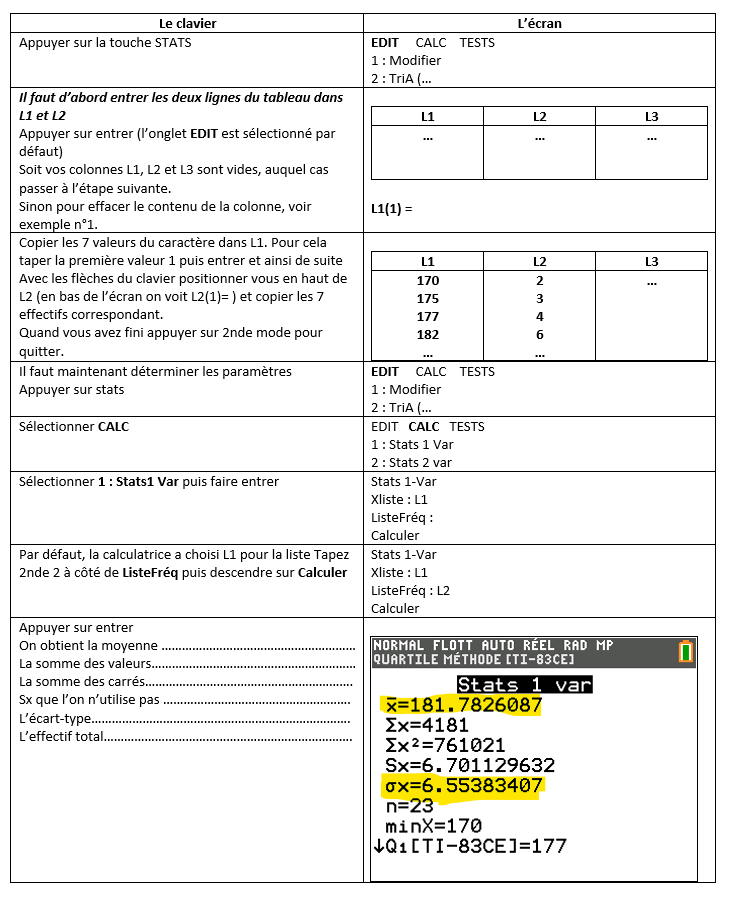
Exercice n°6
On a relevé la fréquence cardiaque d’un goupe de personnes après une séance d’entraînement.

Calculer la moyenne et l’écart-type.
Exercice n°7
On teste une machine qui remplit automatiquement des yaourts contenant 110 g de produit. On pèse 100 yaourts et on obtient le tableau suivant.

Calculer la moyenne et l’écart-type.
Médiane et écart interquartile.
Définition 3
Soit une série d’effectif total N dont les valeurs sont rangées dans l’ordre croissant.
Si N est impair, la médiane notée Me est la valeur centrale de la série.
Si N est pair, la médiane notée Me est la moyenne des valeurs centrales de la série.
Propriété 2
50% des valeurs de la série sont inférieures ou égales à la médiane.
Exercice n°2bis
Voici les temps réalisés (en secondes) par 15 élèves de seconde au 500 m.
90 95 102 106 85 120 110 115 116 98 88 111 125 114 116
Déterminer la médiane de cette série.
Exercice n°4bis
Un professeur de mathématiques demande à ses élèves combien d’enfants comporte leur famille. Il présente les données recueillies dans le tableau ci-dessous :

Déterminer la médiane de cette série.
Définition 4
Le premier quartile Q_{1} est la plus petite valeur du caractère telle qu’au moins 25% des valeurs de la série soient inférieures ou égales à Q_{1} .
Le troisième quartile Q_{3} est la plus petite valeur du caractère telle qu’au moins 75% des valeurs de la série soient inférieures ou égales à Q_{3} .
Exercice n°8
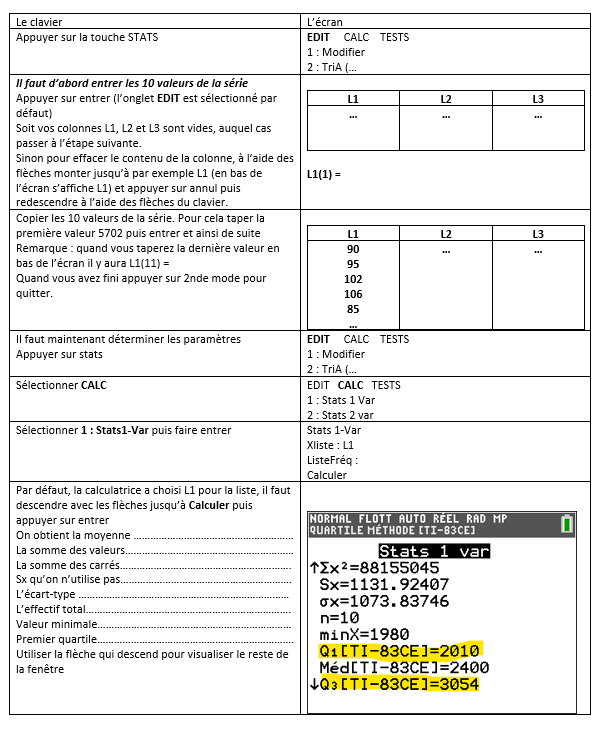
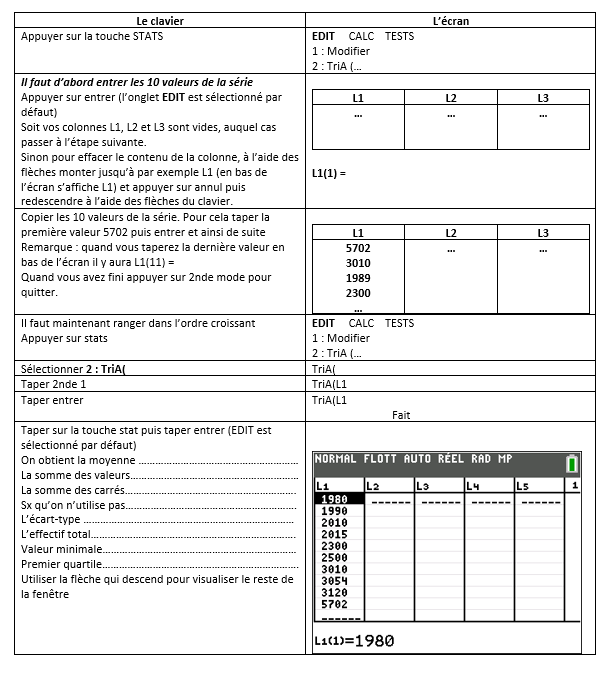
Dans une entreprise de 10 salariés les salaires mensuels ( en euros) sont les suivants :
5702 3010 1980 2300 3054 2010 3120 2500 2015 1990 .
Calculer Q_{1} et Q_{3}.
Exercice n°9
On a demandé à 28 élèves d’une classe de seconde le temps passé sur internet par semaine.
Voici leurs réponses (en heures).

Calculer Q_{1} et Q_{3}.
Définition 5
L’écart interquartile est la différence Q_3-Q_1.
L’intervalle interquartile est l’intervalle [Q_1;Q_3].
Propriété 3
Au moins 50\% des valeurs de la série sont comprises dans l’intervalle interquartile.