logo

2. Probabilités exercices.

Sommaire

Exercice n°1 : des dés à 10 faces

On lance un dé équilibré à 10 faces qu’on lance une seule fois. On note le nombre qui apparaît sur la face supérieure.

1) Quelles sont les issues qui composent l’univers  de cette expérience ? Combien y’en a-t-il ?

correction

2) Citer un évènement élémentaire. Un évènement à deux issues. Un évènement impossible.

correction

3) Quelle est la probabilité de l’évènement A : « obtenir un diviseur de 10 ». Le résultat sera donné sous forme de fraction irréductible.

correction

Exercice n°2 : Des menus

Dans un restaurant, le patron propose un menu à 15 euros.

Ce menu comporte une entrée au choix, un plat au choix et un dessert au choix.

Les entrées sont : assiette de crudités ou œuf mimosa ou terrine du chef.

Les plats sont : entrecôte/ frites ou poisson grillé/riz.

Les desserts sont : tarte maison ou crème brûlée.

On s’intéresse aux menus différents qu’on peut composer.

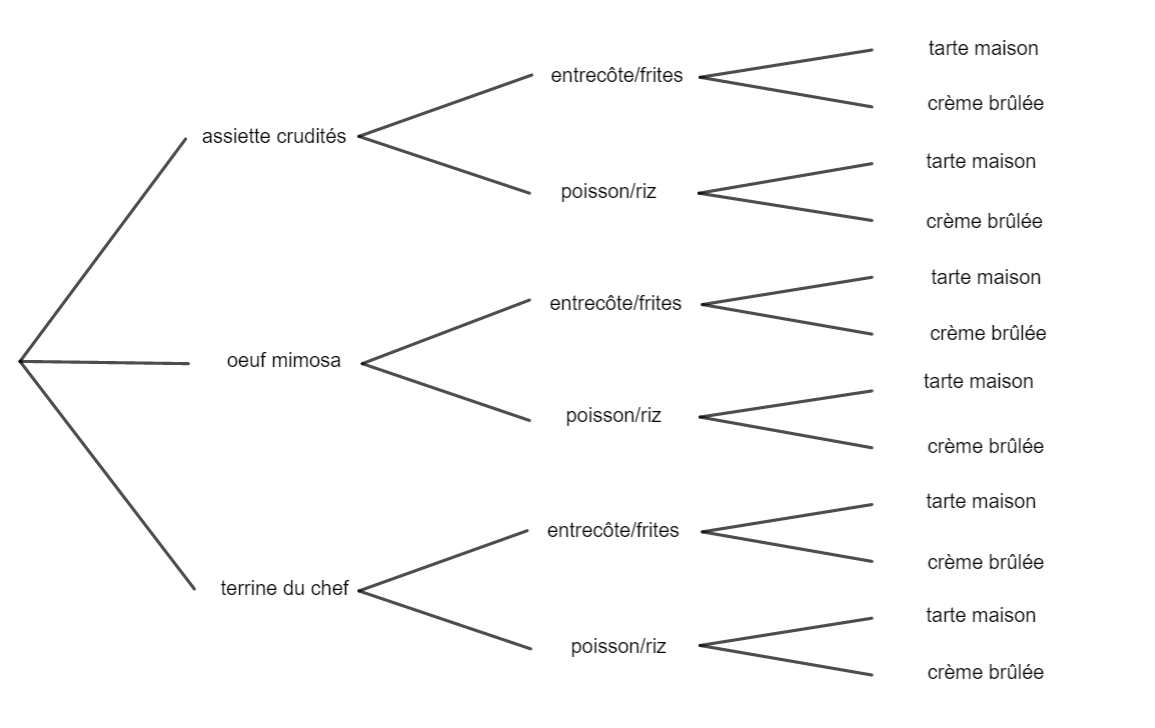
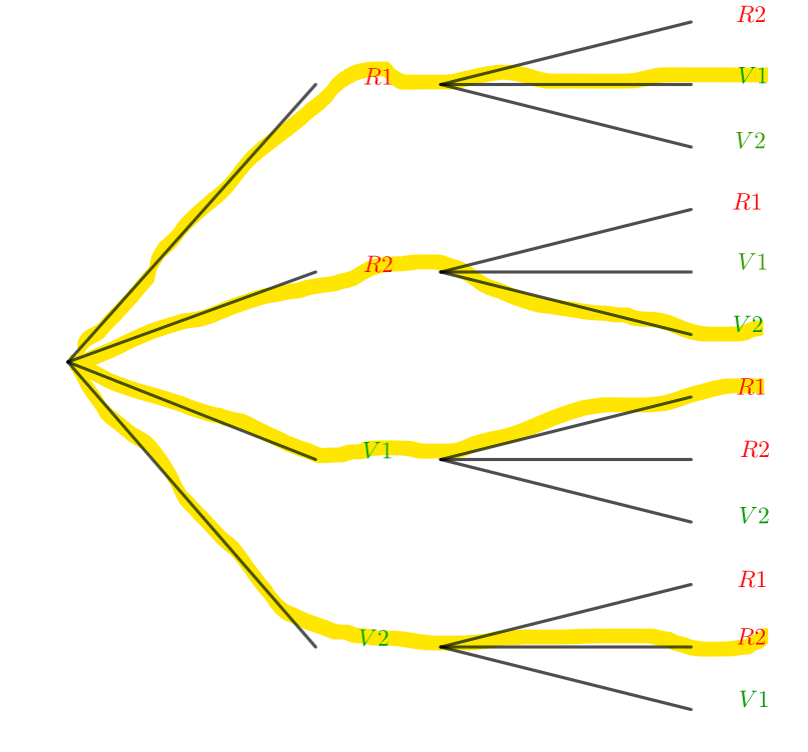
  1. Utiliser un arbre pour matérialiser l’univers de l’expérience.
correction

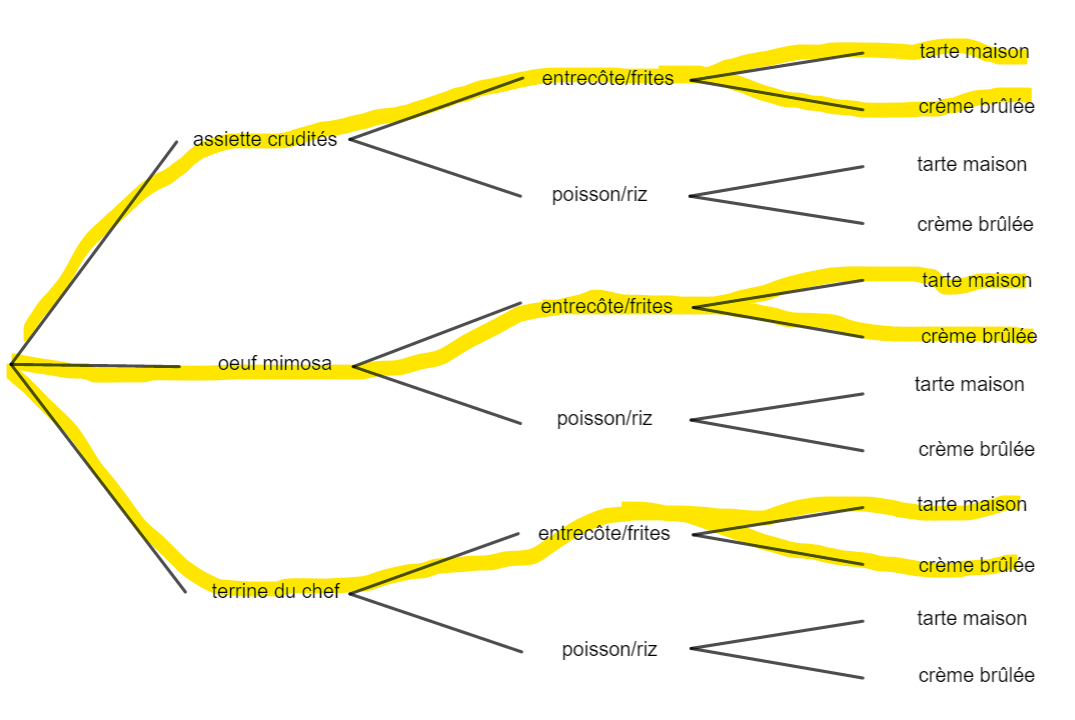
2. Alfred n’aime pas le poisson, quels sont les repas différents qu’il peut composer ?

correction

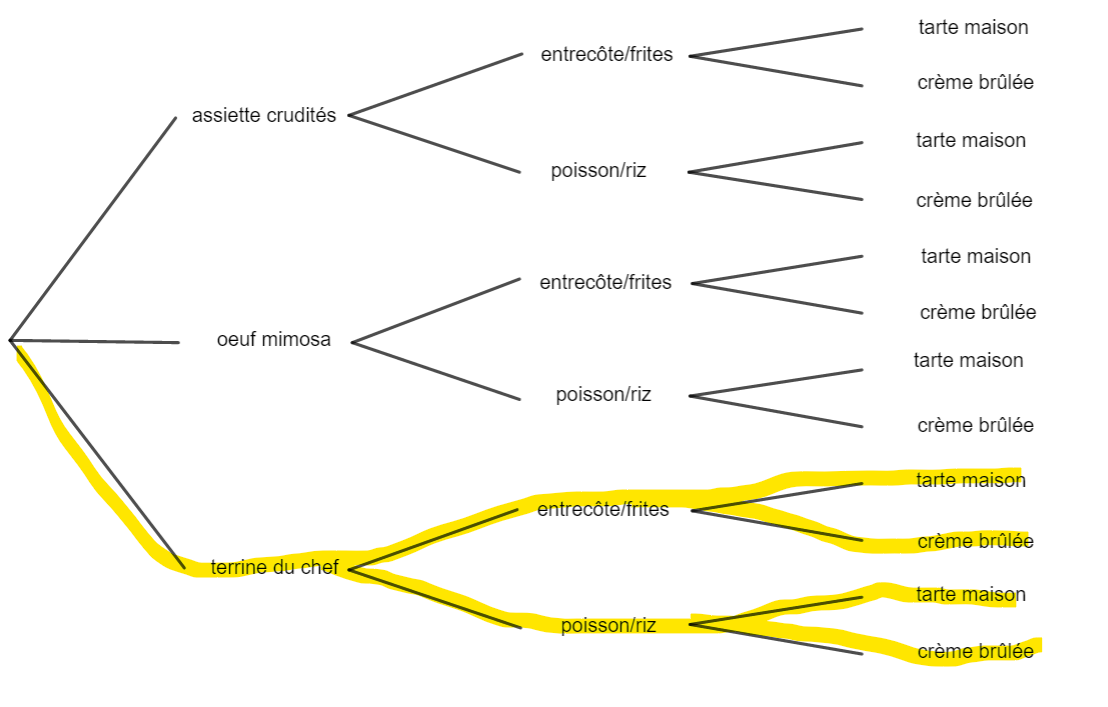
3. Barnabé veut commencer son repas par une terrine du chef, quels sont les repas différents qu’il peut composer ?

correction

4. Quels sont les menus qui peuvent convenir à la fois à Alfred et Barnabé ?

correction

Exercice n°3 :  On jette un dé à six faces de couleur rouge et un dé à six faces de couleur bleue.

On jette les deux dés simultanément.

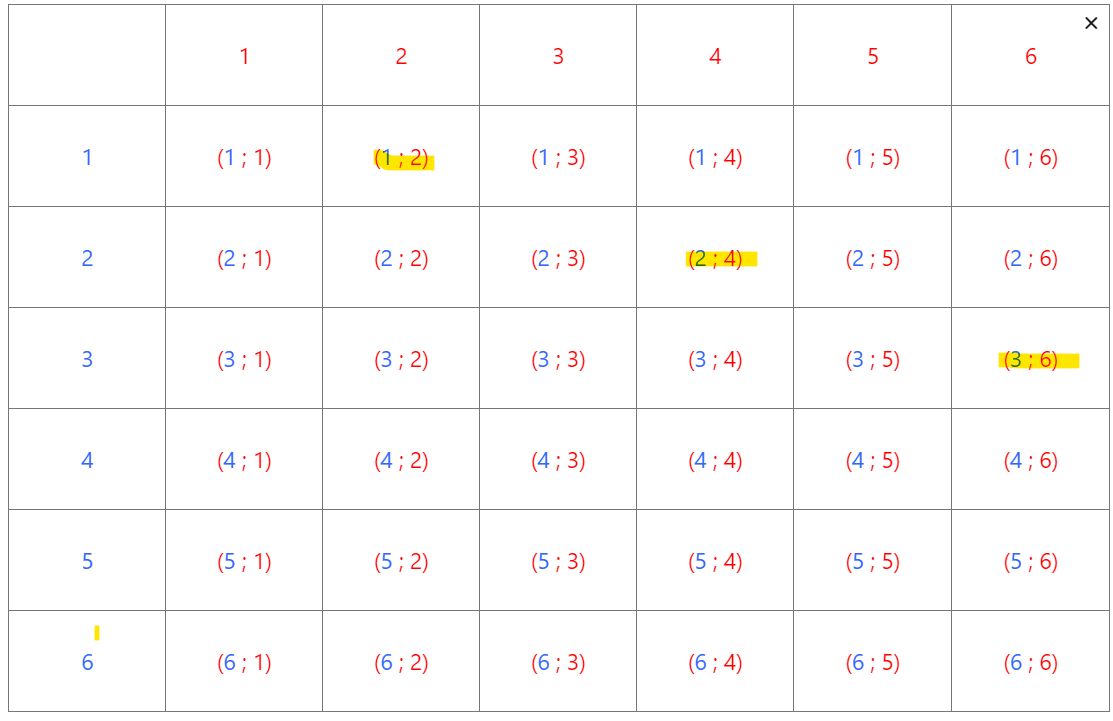
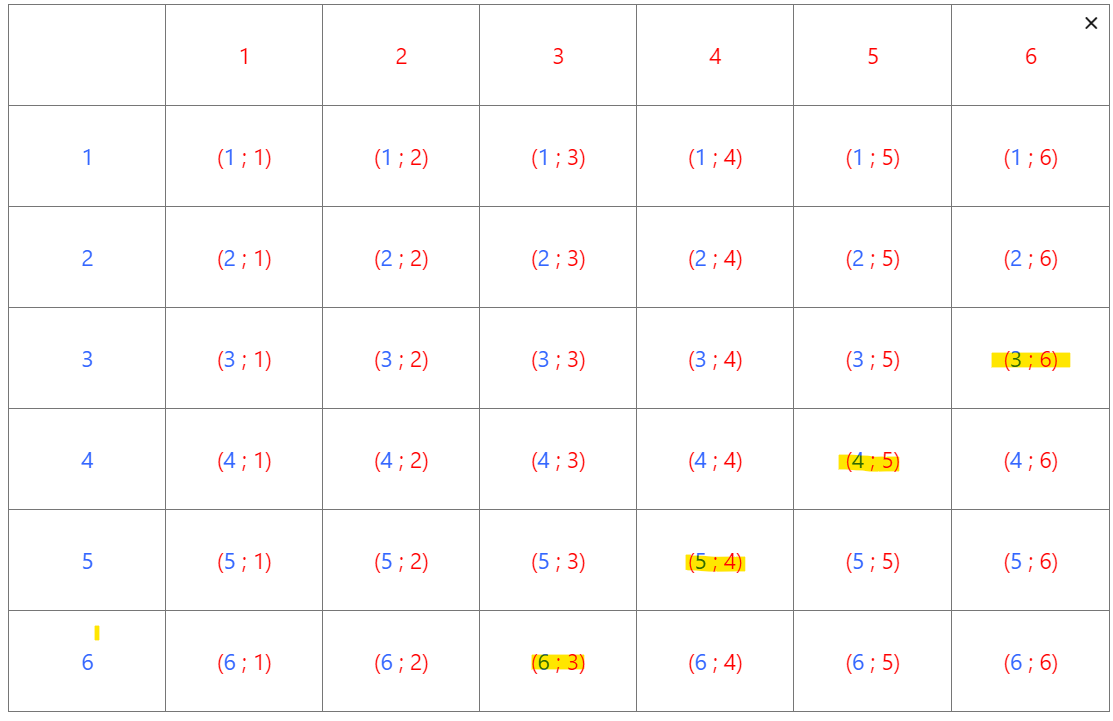
  1. Reproduire et compléter le tableau ci-dessous :

 

1

2

3

4

5

6

1

(1 ; 1)

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

 

 

 

4

 

 

 

 

 

 

5

 

 

 

 

 

 

6

 

 

 

 

 

 

correction

2. On note A l’évènement « le résultat du dé rouge est le double du résultat du dé bleu ». Déterminer les issues composant l’évènement A.

correction

3. On note B l’évènement « la somme des résultats vaut 9 ». Déterminer les issues composant l’évènement B.

correction

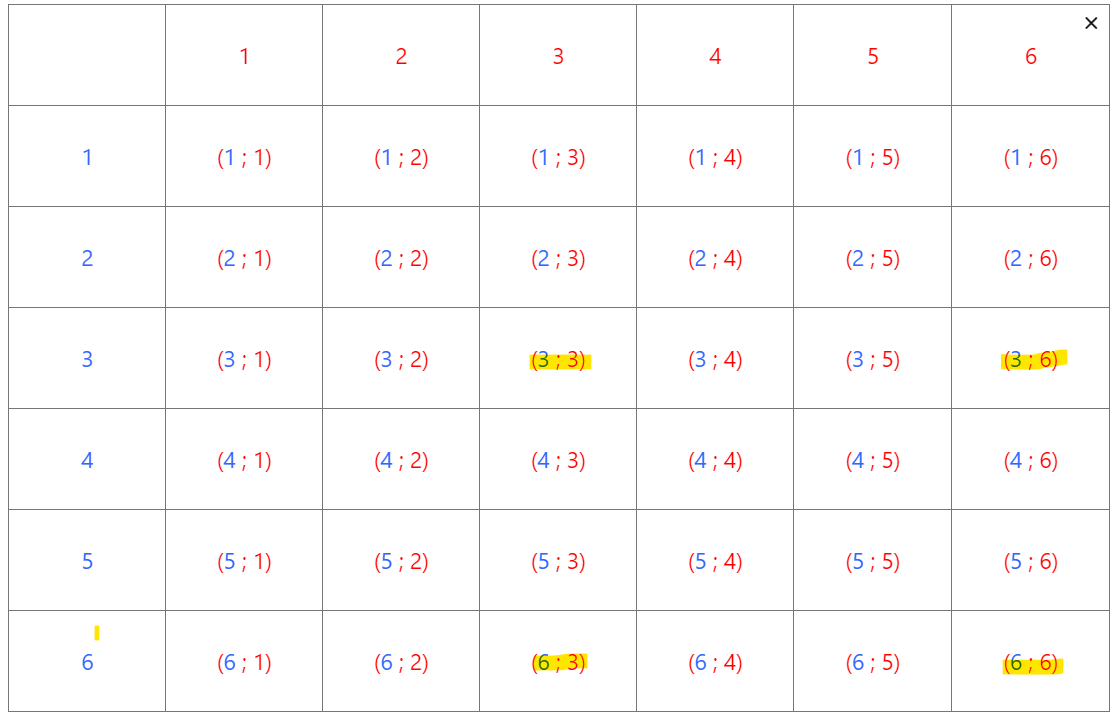
4. On note C l’évènement « les deux résultats sont des multiples de 3 ». Déterminer les issues composant l’évènement C.

correction

5. a) Faire une phrase en français pour caractériser l’évènement B\cap C.

correction

5. b) Déterminer les issues composant l’évènement B\cap C.

correction

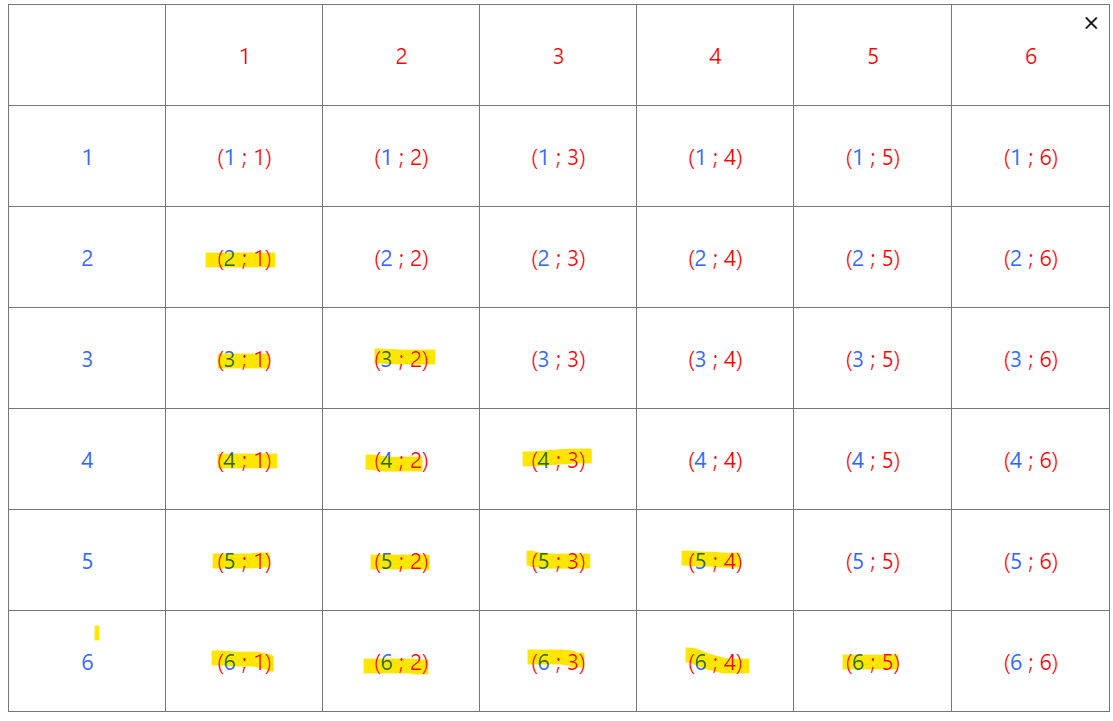
6. On note D l’évènement « le résultat du dé rouge est strictement inférieur au résultat du dé bleu ». Déterminer les issues composant l’évènement D.

correction

7. a) Faire une phrase en français pour caractériser l’évènement \overline D.

correction

7. b) Déterminer les issues composant l’évènement \overline D.

correction

Exercice n°4 : Des jetons carrés, ronds, verts, rouges et bleus.

Dans une urne, se trouvent des jetons carrés, ronds, verts, rouges et bleus.

Parmi les 12 jetons rouges, il y en a autant de carrés que de ronds.

Il y a 12 jetons bleus. Parmi ceux-ci, 9 sont ronds.

Il y a 19 jetons carrés et 15 jetons verts.

Toutes les probabilités seront données sous forme de fraction irréductible.

  1. Compléter le tableau suivant :

                           FORME

COULEUR

CARRES

RONDS

TOTAL

VERT

 

 

 

ROUGE

 

 

 

BLEU

 

 

 

TOTAL

 

 

 

correction

2. On tire un jeton au hasard de l’urne.

a) Calculer les probabilités des évènements suivants.

              « le jeton tiré est bleu »

              « le jeton tiré est rond »

              « le jeton tiré est bleu et rond »

correction : le jeton est bleu
correction : le jeton est rond
correction : le jeton est bleu et rond

b) En déduire la probabilité de l’évènement « le jeton tiré est bleu ou rond »

correction

3. On tire un jeton au hasard parmi les jetons ronds, quelle est la probabilité qu’il soit bleu.

correction

4. On tire un jeton au hasard parmi les jetons rouges, quelle est la probabilité qu’il soit carré.

correction

Exercice n°5 :  Dans une classe de 33 élèves 

2 font de l’italien, de l’anglais et de l’espagnol ;

5 font de l’anglais et de l’espagnol

6 font de l’anglais et de l’italien

5 font de l’italien et de l’espagnol

6 font uniquement de l’espagnol

17 font de l’anglais et 14 font de l’italien

2 ne pratiquent aucune langue vivante.

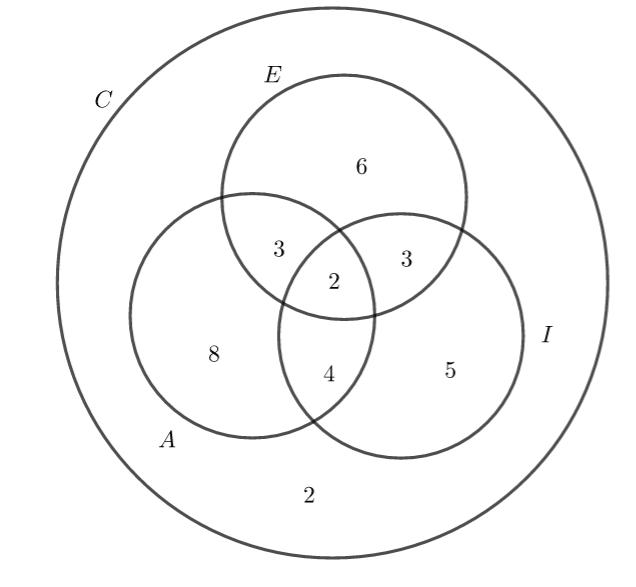
  1. Compléter le diagramme de Venn ci-dessous à l’aide des données de l’énoncé.
correction

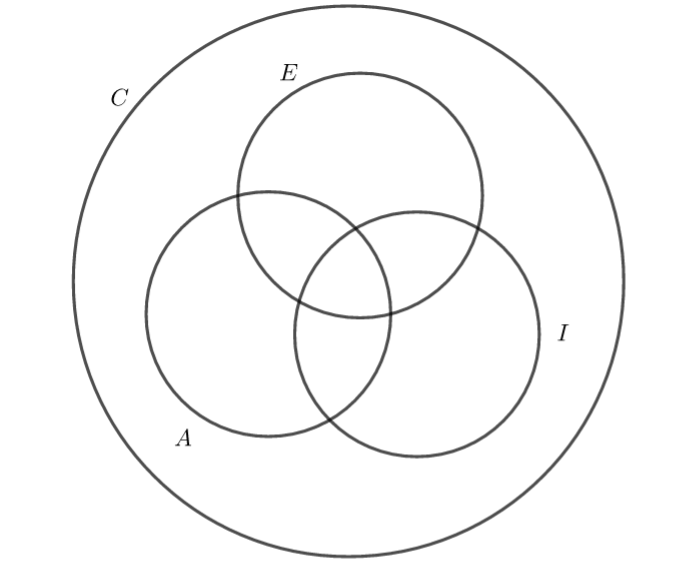
2. On choisit un élève au hasard dans la classe, calculer les probabilités des évènements suivants :

B : l’élève choisi pratique les trois langues

D : l’élève choisi pratique l’anglais et l’espagnol

F : l’élève choisi pratique exactement deux langues

G : l’élève choisi pratique seulement l’anglais

H : l’élève choisi pratique exactement une langue vivante

correction B
correction D
correction F
correction G
correction H

3. On choisit au hasard un élève parmi ceux qui pratiquent l’anglais. Quelle est la probabilité qu’il pratique l’espagnol ?

correction

4. On choisit au hasard un élève parmi ceux qui pratiquent l’espagnol. Quelle est la probabilité qu’il pratique l’anglais ?

correction

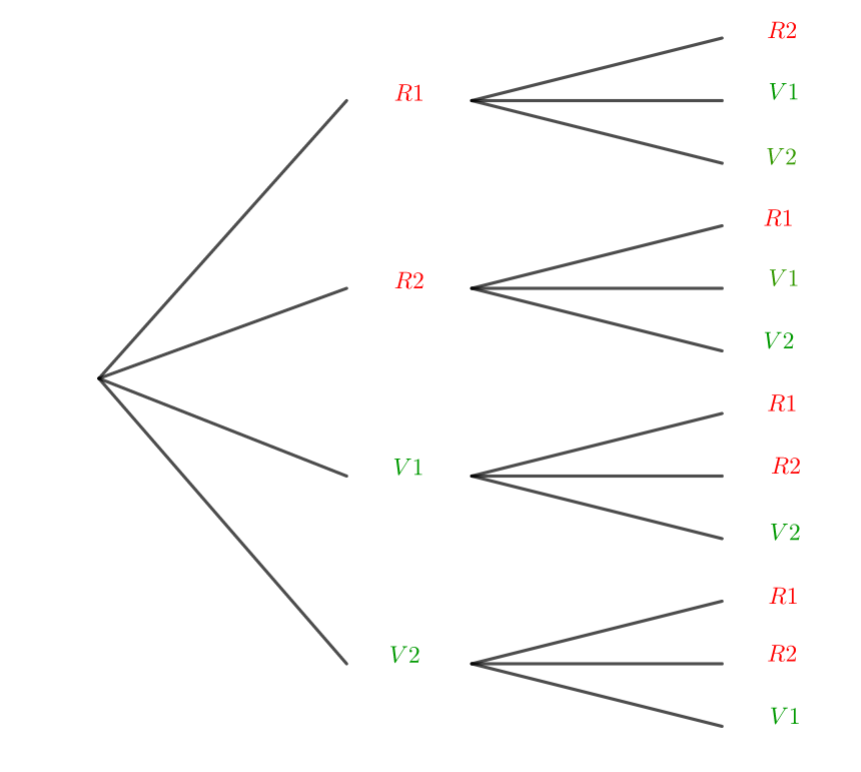
Exercice n°6 : Dans une urne se trouvent deux boules rouges numérotées de 1 à 2 et deux vertes numérotées de 1 à 2.

L’expérience consiste à tirer au hasard une boule de l’urne puis d’en tirer une seconde sans avoir remis la première dans l’urne.

  1. Utiliser un arbre pour matérialiser l’univers de l’expérience.
correction

2) a) Calculer les probabilités des évènements suivants :

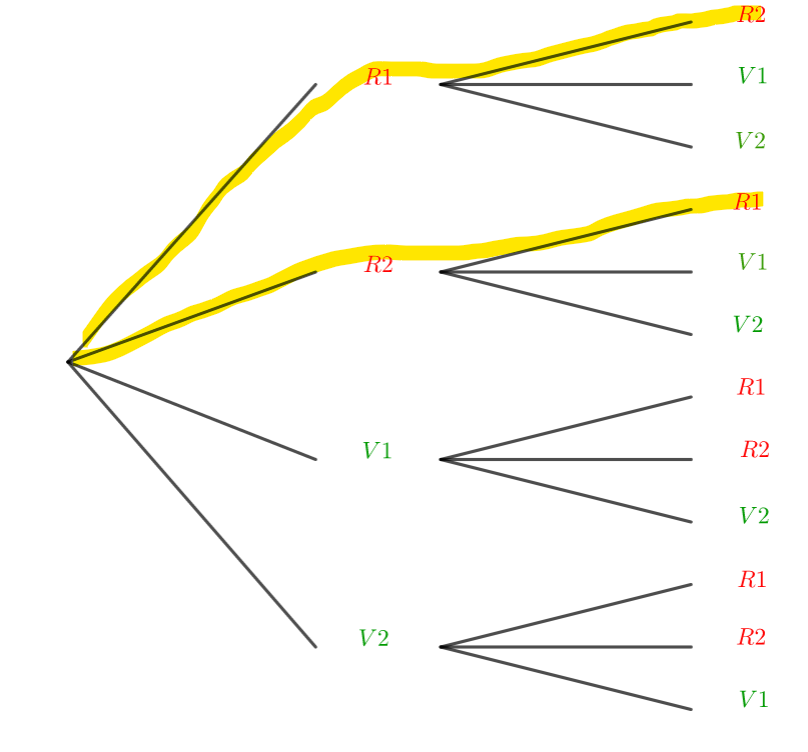
A : les deux boules sont rouges

B : les deux boules sont de même couleur.

C : les deux boules portent le numéro 2.

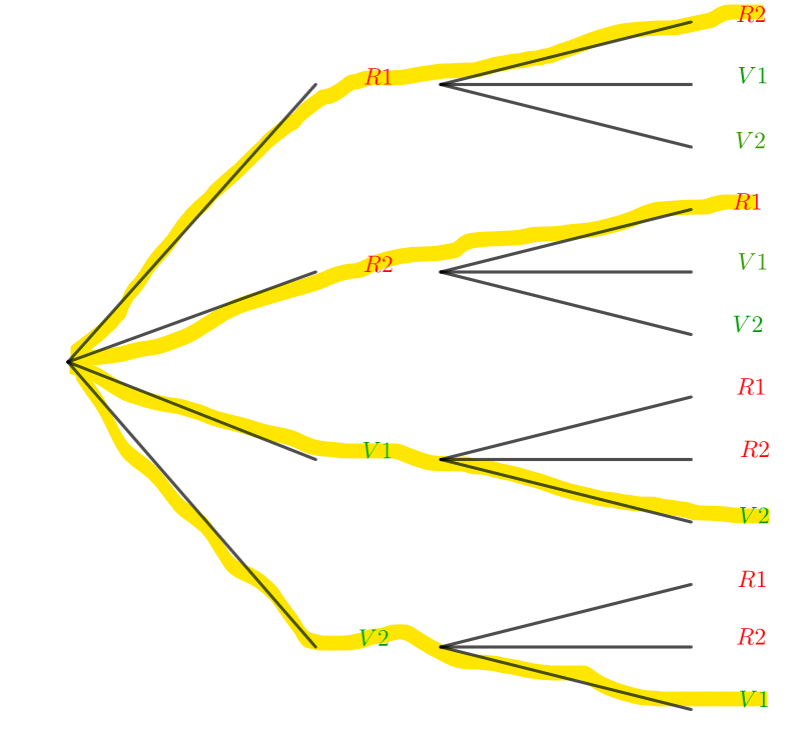
D : les deux boules portent le même numéro.

correction A
correction B
correction C
correction D

  b) Décrire en français l’évènement A\cap D. Puis calculer p(A\cap D)

correction

3) Déduire de la question 2, les probabilités des évènements suivants ( on pourra utiliser l’évènement contraire ou l’évènement A\cup B)

a) Les deux boules sont de couleurs de différentes.

b) Les deux boules ont des numéros différents

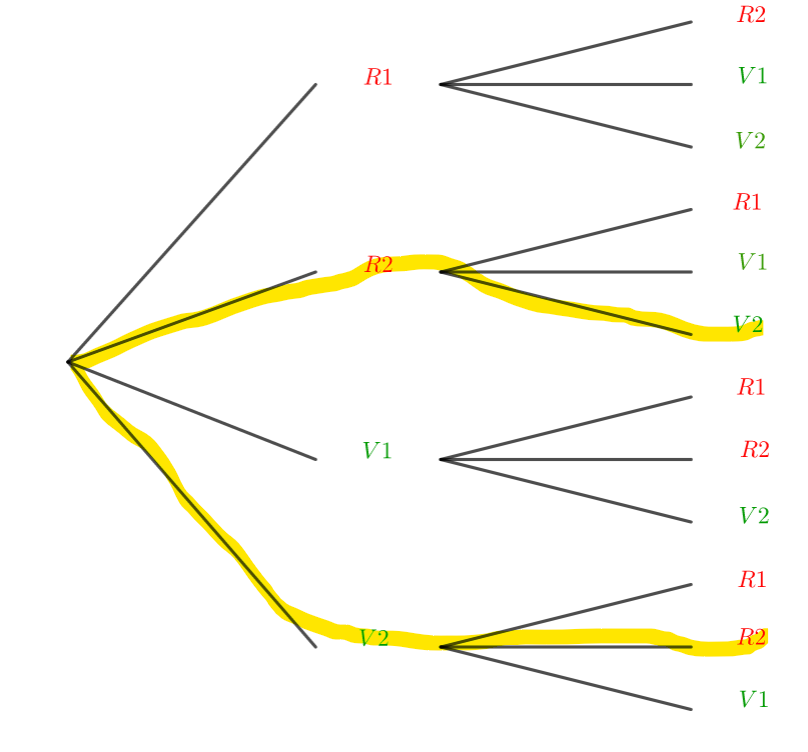
c) Les deux boules sont rouges ou portent le numéro 1

correction 3a
correction 3b
correction 3c

Exercice n°7  

 Dans un club de sport comportant 120 membres, 30% sont des femmes. Chaque membre ne pratique qu’un seul sport.

La moitié des membres fait du tennis, il y a autant de membres  faisant de la natation que de membres faisant du golf.

Il y a deux fois plus de femmes pratiquant la natation que d’hommes pratiquant la natation.

15 % des membres pratiquant le tennis sont des femmes.

  1. Compléter le tableau suivant

 

tennis

natation

golf

total

Femmes

 

 

 

 

 

Hommes

 

 

 

 

 

Total

 

 

 

 

 

correction

2. On choisit au hasard un membre du club.

On note

T : l’évènement : le membre choisi joue au tennis.

N : l’évènement : le membre choisi fait de la natation.

G : l’évènement : le membre choisi joue au golf.

F : l’évènement : le membre choisi est une femme.

H : l’évènement : le membre choisi est un homme.

 Pour les questions suivantes, on attend que vous répondiez en identifiant, quand c’est possible, l’évènement en le notant à l’aide de T, N ,G ,F, H, \cap, \cup,….

a) Calculer la probabilité de choisir un membre qui soit un homme .

Réponse : p ( H ) =

correction

b) Calculer la probabilité de choisir un membre qui fasse de la natation.

correction

c) Calculer la probabilité de choisir un membre qui soit un homme et qui joue au tennis.

correction

d) Calculer la probabilité de choisir un membre qui soit une femme et qui ne joue pas au tennis.

correction

3)  On choisit au hasard un membre du club parmi les hommes. Calculer la probabilité de choisir un membre qui  joue au tennis.

correction

4)  On choisit au hasard un membre du club parmi les membres qui jouent au golf. Calculer la probabilité de choisir une femme.

correction

5) On choisit au hasard un membre du club parmi les membres qui pratiquent la natation. Calculer la probabilité de choisir une femme.

correction

©2020 – Math’O karé SAS

Ici il n’y a pas besoin d’arbre, de tableau ou de diagramme de Venn pour matérialiser l’univers. On peut l’écrire par extension, c’est-à-dire qu’on écrit toutes les issues dans un ensemble.

\Omega=\{1;2;3;4;5;6;7;8;9;10\}

Il y en a 10

Un évènement élémentaire contient une issue.

Un évènement élémentaire possible : « obtenir le 8 ».

Un évènement à deux issues possible : « obtenir le 2 ou le 5 »

Un autre évènement à deux issues possible ; « obtenir un diviseur de 5 « . En effet seuls 1 et 5 divisent 5.

Un évènement impossible : « obtenir 11 »

Les diviseurs de 10 sont 1, 2, 5 et 10.

On est dans une situation d’équiprobabilité donc comme il y a 10 issues différentes dans l’univers, la probabilité d’un évènement élémentaire ( une seule issue) vaut \frac{1}{10}.

Comme l’évènement A comporte 4 issues, p(A)=\frac{4}{10}  .

Pour obtenir la fraction irréductible, il faut simplifier par 2 en haut et en bas.

p(A)=\frac{2}{5}

Voici l’arbre:

On appelle A, l’ensemble des menus qui conviennent à Alfred.

C’est-à-dire ceux qui ne contiennent pas de poisson. On les surligne sur l’arbre ( l’arbre est long à faire mais il permet de répondre rapidement aux questions)

A={crudités/entrecôte/tarte ;  crudités/entrecôte/crème ; oeuf/entrecôte/tarte ;  oeuf/entrecôte/crème ; terrine/entrecôte/tarte ;  terrine/entrecôte/crème }

On appelle B, l’ensemble des menus qui conviennent à Barnabé.

C’est-à-dire ceux qui commencent par la terrine du chef. On les surligne sur l’arbre ( l’arbre est long à faire mais il permet de répondre rapidement aux questions)

B={terrine/entrecôte/tarte ;  terrine/entrecôte/crème ; terrine/poisson/tarte ;  terrine/poisson/crème }

Dans la consigne, on identifie le et accentué par le à la fois. On va donc déterminer l’évènement A\cap B. Il suffit de déterminer les issues contenues dans A et dans B.

A\cap B={ terrine/entrecôte/tarte ;  terrine/entrecôte/crème }

 

1

2

3

4

5

6

1

(1 ; 1)

(1 ; 2)

(1 ; 3)

(1 ; 4)

(1 ; 5)

(1 ; 6)

2

(2 ; 1)

(2 ; 2)

(2 ; 3)

(2 ; 4)

(2 ; 5)

(2 ; 6)

3

(3 ; 1)

(3 ; 2)

(3 ; 3)

(3 ; 4)

(3 ; 5)

(3 ; 6)

4

(4 ; 1)

(4 ; 2)

(4 ; 3)

(4 ; 4)

(4 ; 5)

(4 ; 6)

5

(5 ; 1)

(5 ; 2)

(5 ; 3)

(5 ; 4)

(5 ; 5)

(5 ; 6)

6

(6 ; 1)

(6 ; 2)

(6 ; 3)

(6 ; 4)

(6 ; 5)

(6 ; 6)

 A est l’évènement « le résultat du dé rouge est le double du résultat du dé bleu ». On peut surligner les issues qui conviennent comme ci-dessous:

A= \{(1 ; 2) ; (2 ; 4) ; (3 ; 6) \}

On note B l’évènement « la somme des résultats vaut 9 ». Déterminer les issues composant l’évènement B. On peut surligner les issues qui conviennent comme ci-dessous:

B= \{(6 ; 3) ; (5 ; 4) ; (4 ; 5) ; (3 ; 6)\}

On note C l’évènement « les deux résultats sont des multiples de 3 . On peut surligner les issues qui conviennent comme ci-dessous:

C= \{(3 ; 3) ; (3 ; 6) ; (6 ;3) ; (6 ; 6)\}

Il faut faire une phrase en français pour caractériser l’évènement B\cap C

Les deux résultats sont des multiples de 3 et la somme des résultats vaut 9.

Il suffit de déterminer les issues qui sont à la fois dans B et dans C.

B\cap C =\{(3 ; 6) ; (6 ;3) \}

 

On note D l’évènement « le résultat du dé rouge est strictement inférieur au résultat du dé bleu ». On peut surligner les issues qui conviennent comme ci-dessous.

D= \{(2 ; 1) ; (3 ; 1) ; (3 ;2) ; (4 ; 1) ;(4 ; 2) ; (4 ; 3) ; (5 ;1) ; (5 ; 2) ; (5 ; 3) ; (5 ; 4) ; (6 ;1) ; (6 ; 2) ; (6 ; 3) ; (6 ; 4) ; (6 ;5) \}

Il faut faire une phrase en français pour caractériser l’évènement \overline D.

Le résultat du dé rouge est supérieur ou égal  au résultat du dé bleu .

Il suffit de déterminer les issues qui ne sont pas dans D.

\overline D= \{(1 ; 1) ; (1 ; 2) ; (1 ;3) ; (1 ; 4) ;(1 ; 5) ; (1 ; 6) ; (2 ;2) ; (2 ; 3) ; (2 ; 4) ; (2 ; 5) ; (2 ;6) ; (3 ; 3) ; (3 ; 4) ; (3 ; 5) ; (3 ;6) ) ; (4 ;4) ; (4 ; 5) ; (4 ; 6) ; (5 ; 5) ; (5 ;6) ; (6 ; 6) \}

On commence par remplir les cases à l’aide des nombres de l’énoncé :

                           FORME

COULEUR

CARRES

RONDS

TOTAL

VERT

 

 

15

ROUGE

 

 

12

BLEU

 

9

12

TOTAL

19

 

 

Pour poursuivre on exploite la donnée « Parmi les 12 jetons rouges, il y en a autant de carrés que de ronds. »

Il y aura donc 6 ronds rouges et 6 carrés rouges.

                           FORME

COULEUR

CARRES

RONDS

TOTAL

VERT

  

15

ROUGE

6

6

12

BLEU

 

9

12

TOTAL

19

  

Pour finir, il suffit d’ajouter et de soustraire.

                           FORME

COULEUR

CARRES

RONDS

TOTAL

VERT

10

5

15

ROUGE

6

6

12

BLEU

3

9

12

TOTAL

19

20

39

Il y a 39 jetons au total, le tirage est équiprobable donc chaque jeton a une probabilité  \frac{1}{39} d’être choisi.

Il y a 12 jetons bleus qui ont tous une probabilité \frac{1}{39}  d’être choisi.

p(« le jeton tiré est bleu ») =\frac{12}{39} 

On simplifie par 3 .

p(« le jeton tiré est bleu ») = \frac{4}{13} 

 

Il y a 39 jetons au total, le tirage est équiprobable donc chaque jeton a une probabilité  \frac{1}{39} d’être choisi.

Il y a 20 jetons ronds qui ont tous une probabilité \frac{1}{39}  d’être choisi.

p(« le jeton tiré est rond ») =\frac{20}{39} 

Il y a 39 jetons au total, le tirage est équiprobable donc chaque jeton a une probabilité  \frac{1}{39} d’être choisi.

Il y a 9 jetons bleus et ronds qui ont tous une probabilité \frac{1}{39}  d’être choisi.

p(« le jeton tiré est bleu et rond ») =\frac{9}{39} 

On simplifie par 3 .

p(« le jeton tiré est bleu et rond ») = \frac{3}{13} 

On applique la formule du cours : p(A\cup B)=p(A)+p(B)-p(A\cap B)

p(« le jeton tiré est bleu ou rond »)= p(« le jeton tiré est bleu ») +p(« le jeton tiré est rond »)- p(« le jeton tiré est bleu et rond »)

p(« le jeton tiré est bleu ou rond »)=\frac{4}{13}+\frac{20}{39}-\frac{3}{13}

Pour ajouter les fractions, on les met au même dénominateur , ici 39.

p(« le jeton tiré est bleu ou rond »)=\frac{12}{39}+\frac{20}{39}-\frac{9}{39}

p(« le jeton tiré est bleu ou rond »)=\frac{12+20-9}{39}

p(« le jeton tiré est bleu ou rond »)=\frac{23}{39}

Attention l’expérience change, l’univers change aussi.

Il y a 20 jetons ronds au total, le tirage est équiprobable donc chaque jeton a une probabilité  \frac{1}{20} d’être choisi.

Parmi les 20 jetons ronds,  y a 9 jetons bleus qui ont tous une probabilité \frac{1}{20}  d’être choisi.

p(« le jeton tiré est bleu ») =\frac{9}{20} 

Attention l’expérience change, l’univers change aussi.

Il y a 12 jetons rouges au total, le tirage est équiprobable donc chaque jeton a une probabilité  \frac{1}{12} d’être choisi.

Parmi les 12 jetons rouges,  y a 6 jetons carrés qui ont tous une probabilité \frac{1}{12}  d’être choisi.

p(« le jeton tiré est carré ») =\frac{6}{12} 

On simplifie par 6.

p(« le jeton tiré est carré ») =\frac{1}{2} 

Pour remplir un diagramme de ce type, il faut commencer par l’intérieur et aller vers l’extérieur comme en calligraphie  chinoise.

La partie commune aux trois évènements correspond à l’intersection des trois ensembles : le nombre 2 correspond nombre d’ élèves qui font de l’italien, de l’anglais et de l’espagnol 

La partie commune aux évènements A et E correspond aux 5 élèves  qui font de l’anglais et de l’espagnol. Attention ces 5 élèves se partagent en 2 qui font de l’italien, de l’anglais et de l’espagnol  et 3 qui font de l’anglais et de l’espagnol  mais pas d’italien.

La partie commune aux évènements A et I correspond aux 6 élèves  qui font de l’anglais et de l’italien. Attention ces 6 élèves se partagent en 2 qui font de l’italien, de l’anglais et de l’espagnol  et 4 qui font de l’anglais, de l’italien mais pas d’espagnol.

La partie commune aux évènements E et I correspond aux 5 élèves  qui font de l’espagnol et de l’italien. Attention ces 5 élèves se partagent en 2 qui font de l’italien, de l’anglais et de l’espagnol  et 3 qui font de l’espagnol, de l’italien mais pas d’anglais.

Dans la partie A , hors des parties E et I, on a les élèves qui font uniquement de l’anglais,

il y en a 17-3-4-2=8

Dans la partie E , hors des parties A et I, on a les élèves qui font uniquement de l’espagnol,

il y en a 14-3-3-2=6

Dans la partie I, hors des parties E et A, on a les élèves qui font uniquement de l’italien,

il y en a 14-3-4-2=5

Dans la partie C hors des parties A, B et C, il y a les 2 élèves qui ne pratiquent aucune langue vivante.

Il y a 33 élèves au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{33} d’être choisi.

Il y a 2 élèves qui pratiquent les trois langues,  ils ont tous une probabilité \frac{1}{33}  d’être choisi.

p(B)=\frac{2}{33}

Il y a 33 élèves au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{33} d’être choisi.

Il y a 5 élèves qui pratiquent l’anglais et l’espagnol,  ils ont tous une probabilité \frac{1}{33}  d’être choisi.

p(D)=\frac{5}{33}

Il y a 33 élèves au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{33} d’être choisi.

Il y a 4+3+3 élèves qui pratiquent exactement deux langues,  ils ont tous une probabilité \frac{1}{33}  d’être choisi.

p(F)=\frac{4+3+3}{33}\\p(F)=\frac{10}{33}

Il y a 33 élèves au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{33} d’être choisi.

Il y a 8 élèves qui pratiquent uniquement l’anglais,  ils ont tous une probabilité \frac{1}{33}  d’être choisi.

p(G)=\frac{8}{33}

Il y a 33 élèves au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{33} d’être choisi.

Il y a 8+6+5 élèves qui pratiquent uniquement une langue vivante,  ils ont tous une probabilité \frac{1}{33}  d’être choisi.

p(H)=\frac{8+6+5}{33}\\p(H)=\frac{19}{33}

Il y a 17 élèves qui pratiquent l’anglais au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{17} d’être choisi.

 Parmi ceux-là il y a 5 élèves qui pratiquent l’espagnol,  ils ont tous une probabilité \frac{1}{17}  d’être choisi.

 Ainsi si on choisit un élève qui pratique l’anglais, la probabilité qu’il pratique l’espagnol est \frac{5}{17} 

Il y a 14 élèves qui pratiquent l’espagnol au total, le tirage est équiprobable donc chaque élève a une probabilité  \frac{1}{14} d’être choisi.

 Parmi ceux-là il y a 5 élèves qui pratiquent l’anglais,  ils ont tous une probabilité \frac{1}{14}  d’être choisi.

 Ainsi si on choisit un élève qui pratique l’espagnol, la probabilité qu’il pratique l’anglais est \frac{5}{14} 

Les branches primaires de l’arbre représentent les choix possibles pour le premier tirage de boules; les branches secondaires de l’arbre représentent les choix possibles pour le deuxième tirage de boules sachant que l’on n’a pas remis la première boule dans l’urne.

A : les deux boules sont rouges

On a recensé 12 issues différentes à l’aide de l’arbre. Chaque issue a une probabilité \frac{1}{12} de se produire. On détermine les issues qui composent l’évènement A à l’aide de l’arbre ci-dessous.

A=\{(R1;R2);(R2;R1)\}.

Il y a deux issues dans l’évènement A, chacune d’elles a une probabilité \frac{1}{12} de se produire.

p(A)=\frac{2}{12}

On simplifie par 2 en haut et en bas.

p(A)=\frac{1}{6}

B : les deux boules sont de même couleur.

On a recensé 12 issues différentes à l’aide de l’arbre. Chaque issue a une probabilité \frac{1}{12} de se produire. On détermine les issues qui composent l’évènement B à l’aide de l’arbre ci-dessous.

B={R1R2;R2R1;V1V2;V2V1}

Il y a 4 issues dans l’évènement B, chacune d’elles a une probabilité \frac{1}{12} de se produire.

p(B)=\frac{4}{12}

On simplifie par 4 en haut et en bas.

p(B)=\frac{1}{3}

C : les deux boules portent le numéro 2.

On a recensé 12 issues différentes à l’aide de l’arbre. Chaque issue a une probabilité \frac{1}{12} de se produire. On détermine les issues qui composent l’évènement C à l’aide de l’arbre ci-dessous.

C=\{(R2;V2);(V2;R2)\}.

Il y a deux issues dans l’évènement C, chacune d’elles a une probabilité \frac{1}{12} de se produire.

p(C)=\frac{2}{12}

On simplifie par 2 en haut et en bas.

p(C)=\frac{1}{6}

D : les deux boules portent le même numéro.

On a recensé 12 issues différentes à l’aide de l’arbre. Chaque issue a une probabilité \frac{1}{12} de se produire. On détermine les issues qui composent l’évènement D à l’aide de l’arbre ci-dessous.

D=\{(R1;V1);(R2;V2)(V1;R1);(V2;R2)

Il y a 4 issues dans l’évènement D, chacune d’elles a une probabilité \frac{1}{12} de se produire.

p(D)=\frac{4}{12}

On simplifie par 4 en haut et en bas.

p(D)=\frac{1}{3}

L’évènement A\cap D correspond à l’évènement les deux boules tirées sont rouges et portent le numéro1.

C’est un évènement impossible donc p(A\cap D)=0

On remarque que les évènements A et D sont incompatibles

Les deux boules sont de couleurs de différentes.

Cet évènement est le contraire de B, on le note \overline B.

On applique la formule : p(\overline B)=1-p(B)

p(\overline B)=1-\frac{1}{3}

Pour faire la différence, on met au même dénominateur ; ici 3.

p(\overline B)=\frac{3}{3}-\frac{1}{3}

p(\overline B)=\frac{3-1}{3}

p(\overline B)=\frac{2}{3}

Les deux boules ont des numéros différents

Cet évènement est le contraire de D, on le note \overline D.

On applique la formule : p(\overline D)=1-p(D)

p(\overline D)=1-\frac{1}{3}

Pour faire la différence, on met au même dénominateur ; ici 3.

p(\overline D)=\frac{3}{3}-\frac{1}{3}

p(\overline D)=\frac{3-1}{3}

p(\overline D)=\frac{2}{3}

Les deux boules sont rouges ou portent le numéro 1.

On cherche la probabilité de l’évènement A ou D. C’est-à-dire A\cup B.

Les évènements A et D sont incompatibles, donc on applique la formule p(A\cup D)=p(A)+p(D).

p(A\cup D)=\frac{1}{6}+\frac{1}{3}.

Pour effectuer la somme, on met au même dénominateur; ici 6.

p(A\cup D)=\frac{1}{6}+\frac{1\times2}{3\times2}.

p(A\cup D)=\frac{1}{6}+\frac{2}{6}.

p(A\cup D)=\frac{1+2}{6}.

p(A\cup D)=\frac{3}{6}.

On simplifie par 3 en haut et en bas.

p(A\cup D)=\frac{1}{2}.

-J’écris 120 dans la case en bas à droite, c’est le nombre total de tous les membres.

-J’utilise la donnée : « 30% de ces membres sont des femmes » pour calculer le nombre de femmes du club. J’utilise le tableau ci-dessous :

 

effectifs

pourcentages

Partie :

femmes du club

 

30

Tout :

les membres du club

120

100

Pour déterminer le nombre de femmes, j’applique le produit en croix dans le tableau de proportionnalité ci-dessus.

\frac{30\times120}{100}=36

J’indique donc 36 dans la case total Femmes.

– J’utilise la donnée : « la moitié des membres fait du tennis » pour calculer le nombre total de membres qui jouent au tennis.Il y a au total 120 membres donc 60 font du tennis.

J’indique 60 dans la case total tennis.

 – J’utilise la donnée : « il y a autant de membres  faisant de la natation que de membres faisant du golf» pour calculer le nombre total de membres qui jouent au golf et qui pratiquent la natation. Il y a au total 120 membres comme 60 font du tennis, il en reste 60 qui jouent au golf ou qui pratiquent la natation. Comme il y en a autant dans les deux activités : 30 membres font du golf et 30 font de la natation.

J’indique 30 dans la case total golf et 30 dans la case total natation.

– J’utilise la donnée : « Il y a deux fois plus de femmes pratiquant la natation que d’hommes pratiquant la natation.

   Il y a 30 membres qui pratiquent la natation, si on divise en trois : il y aura deux parts pour les femmes c’est-à-dire 20 et une pour les hommes c’est-à-dire 10.

J’indique 20 dans la case natation/Femmes et 10 dans la case natation/Hommes

-J’utilise la donnée : « 15 % des membres pratiquant le tennis sont des femmes.» pour calculer le nombre de femmes qui font du tennis. J’utilise le tableau ci-dessous :

 

effectifs

pourcentages

Partie :

femmes qui font du tennis

 

15

Tout :

membres jouant au tennis

60

100

Pour déterminer le nombre de femmes qui jouent au tennis,  j’applique le produit en croix dans le tableau de proportionnalité ci-dessus.

\frac{15\times 60}{100}=9

J’indique donc 9 dans la case tennis/Femmes.

Pour finir de compléter le tableau, il ne reste plus qu’à soustraire et ajouter.

 

tennis

natation

golf

total

Femmes

 

9

20

7

36

Hommes

 

51

10

23

84

Total

 

60

30

30

120

L’expérience consiste à choisir au hasard un membre du club parmi les 120 membres. Chacun a la probabilité \frac{1}{120} d’être choisi.

On calcule la probabilité de choisir un membre qui soit un homme.

Il y a 84 hommes. Chacun a la probabilité \frac{1}{120}  d’être choisi.

p ( H ) =\frac{84}{120}

On simplifie par 12 en haut et en bas.

p ( H ) =\frac{7}{10}

L’expérience consiste à choisir au hasard un membre du club parmi les 120 membres. Chacun a la probabilité \frac{1}{120} d’être choisi.

On calcule la probabilité de choisir un membre qui fasse de la natation.

Il y a 30 membres qui font de la natation.. Chacun a la probabilité \frac{1}{120}  d’être choisi.

p ( N) =\frac{30}{120}

On simplifie par 30 en haut et en bas.

p ( N ) =\frac{1}{4}

L’expérience consiste à choisir au hasard un membre du club parmi les 120 membres. Chacun a la probabilité \frac{1}{120} d’être choisi.

On calcule la probabilité de choisir un membre qui  soit un homme et qui joue au tennis.

Il y a 51 membres qui sont des hommes et qui jouent au tennis. Chacun a la probabilité \frac{1}{120}  d’être choisi.

p(H\cap T)=\frac{51}{120}

On simplifie par 3 en haut et en bas.

p(H\cap T)=\frac{17}{40}

L’expérience consiste à choisir au hasard un membre du club parmi les 120 membres. Chacun a la probabilité \frac{1}{120} d’être choisi.

On calcule la probabilité de choisir un membre qui  soit une femme et qui ne joue pas au tennis.

Il y a 27 membres qui sont des femmes et qui ne jouent pas au tennis. Chacune a la probabilité \frac{1}{120}  d’être choisi.

p(F\cap {\overline T})=\frac{27}{120}

On simplifie par 3 en haut et en bas.

p(F\cap {\overline T})=\frac{9}{40}

L’expérience a changé dans cette question. On choisit un membre parmi les hommes du club.

L’univers de l’expérience est constitué de tous les hommes du club. Chacun a une probabilité \frac{1}{84} d’être choisi.

 On veut calculer la probabilité de choisir un membre qui  joue au tennis.

Il y a 51 membres qui jouent au tennis parmi les hommes du club.

La probabilité de choisir un membre qui joue au tennis parmi les hommes du club est \frac{51}{84} ou \frac{17}{28}.

L’expérience a changé dans cette question. On choisit un membre parmi les membres qui jouent au golf.

L’univers de l’expérience est constitué de tous les membres du club qui jouent au golf. Chacun a une probabilité \frac{1}{30} d’être choisi.

 On veut calculer la probabilité de choisir une femme .

Il y a 7 femmes parmi les membres qui jouent au golf..

La probabilité de choisir une femme parmi les golfeurs du club est \frac{7}{30} .

L’expérience a changé dans cette question. On choisit un membre parmi les membres qui pratiquent la natation.

L’univers de l’expérience est constitué de tous les membres du club qui pratiquent la natation. Chacun a une probabilité \frac{1}{30} d’être choisi.

 On veut calculer la probabilité de choisir une femme .

Il y a 20 femmes parmi les membres qui pratiquent la natation.

La probabilité de choisir une femme parmi les nageurs est \frac{20}{30} ou \frac{2}{3}.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.