logo

2.Algorithmique et programmation.Exercices.

Exercice n°1: Voici un programme écrit en langage Python.

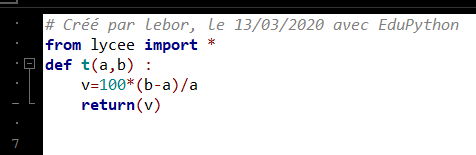
  1. Quel est le nom de la fonction ? Combien possède-elle d’arguments ? 
correction

2. Quelle sortie obtient-on si on entre dans la console 

t(100,300)

t(125, 25)

t(400,500)

correction

3. En utilisant les définitions de la leçon information chiffrée, faire une phrase en Français pour expliquer ce que fait cet algorithme. 

correction

Exercice n°2: Voici un programme écrit en langage Python.

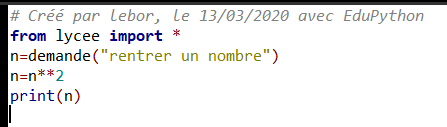
1. Quelle sortie obtient-on si on entre les nombres suivants :

1; -1;3;5;10;100
correction

2. Faire une phrase en Français pour expliquer ce que fait cet algorithme. 

correction

Exercice n°3: Voici un programme écrit en langage Python.

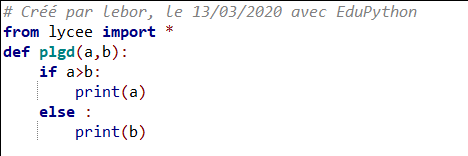
1. Quelle sortie obtient-on si on saisit :

plgd (-4,3), plgd (-2,-3), plgd (3,5), plgd (\sqrt 2,1.42) et plgd (\frac{3}{7},\frac{5}{13})

correction

2. Faire une phrase en Français pour expliquer ce que fait cet algorithme. 

correction

Exercice n°4: Voici un programme écrit en langage Python.

1. Donner deux exemples de résultats obtenus avec cet algorithme.

correction

2. Quelle expérience de probabilité est modélisée par cet algorithme ?

correction

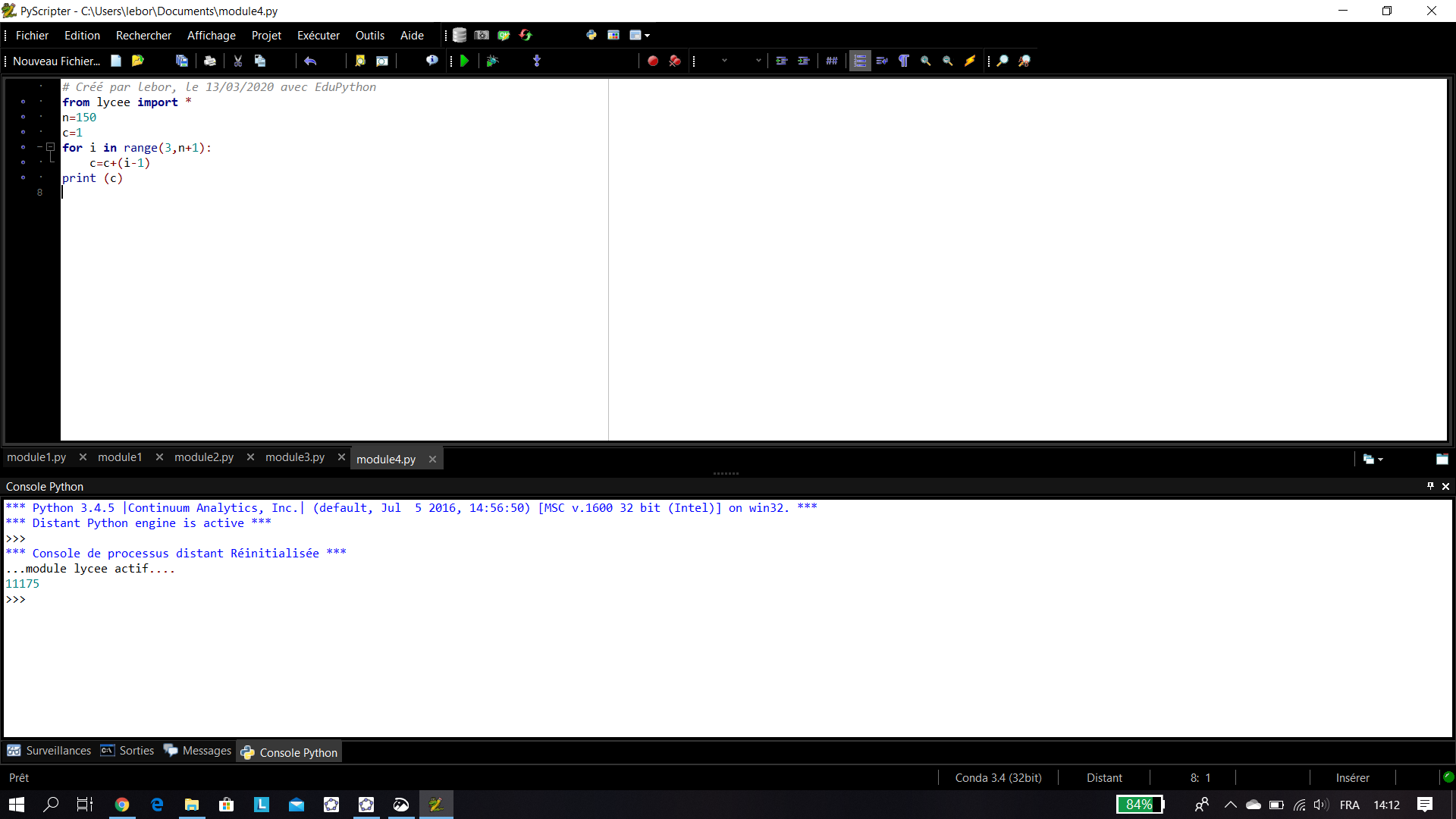
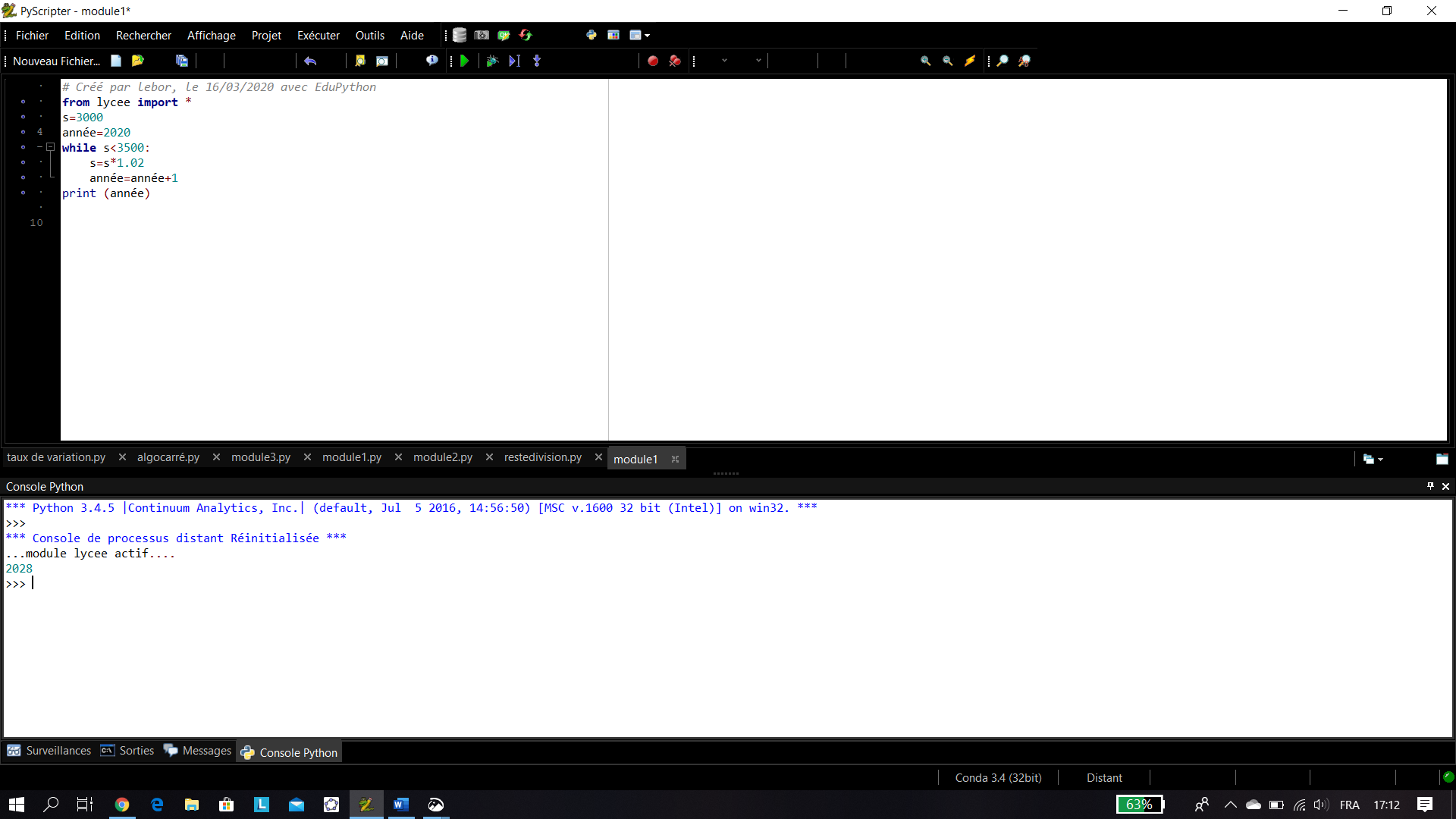
Exercice n°5: Voici un programme écrit en langage Python.

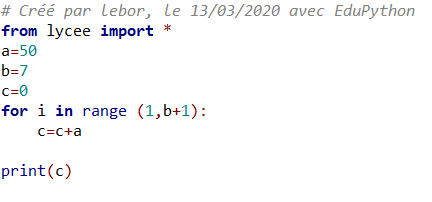
1. Excécuter cet algorithme et donner la valeur en sortie.

correction

2. Faire une phrase en Français pour expliquer ce que fait cet algorithme. 

correction

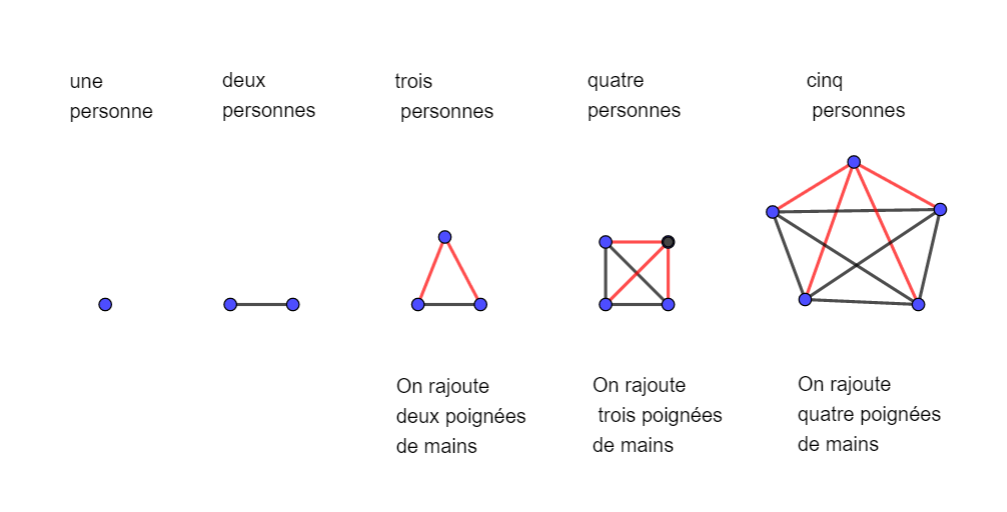
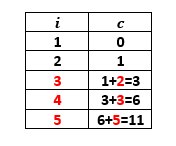
Exercice n°6: Dans une assemblée qui comporte 150 personnes, combien y’a-t-il de poignées de mains échangées en sachant que tous se serrent la main.

correction

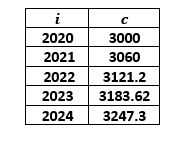
Exercice n°7: On place 3000 euros au taux de 2% au 1er janvier 2020. En quelle année, la somme placée dépassera 3500 euros ?

correction

©2020 – Math’O karé SAS

La fonction s’appelle t.

Elle possède deux arguments a et b.

Quelle valeur en sortie, obtient-on avec t(100,300)= ?

je remplace a par 100 et b par 300 dans t=(b-a)/a

La variable t reçoit la valeur \frac{300-100}{100}

La variable t reçoit la valeur \frac{200}{100}

La variable t reçoit la valeur 2

L’algorithme donne en sortie la valeur 2.

Quelle valeur en sortie, obtient-on avec t(125,25)= ?

je remplace a par 125 et b par 25 dans t=(b-a)/a

La variable t reçoit la valeur \frac{25-125}{125}

La variable t reçoit la valeur -\frac{100}{125}

On peut simplifier en haut et en bas par 25.

La variable t reçoit la valeur -\frac{4}{5}

La variable t reçoit la valeur -0.8

L’algorithme donne en sortie la valeur -0.8.

Quelle valeur en sortie, obtient-on avec t(400,500)= ?

je remplace a par 400 et b par 500 dans t=(b-a)/a

La variable t reçoit la valeur \frac{500-400}{400}

La variable t reçoit la valeur \frac{100}{400}

On peut simplifier en haut et en bas par 100.

La variable t reçoit la valeur \frac{1}{4}

La variable t reçoit la valeur 0.25

L’algorithme donne en sortie la valeur 0.25.

Cet algorithme calcule le taux de variation entre la valeur initiale a et la valeur finale b.

Quelle valeur en  obtient-on en sortie , en entrant la valeur 1 ?

la variable n reçoit d’abord en entrée la valeur1.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 1 (1 élevé au carré)

L’algorithme donne en sortie la valeur 1 (la dernière valeur rentrée dans la case n).

Quelle valeur  obtient-on en sortie, en entrant la valeur -1 ?

la variable n reçoit d’abord en entrée la valeur -1.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 1 (-1 élevé au carré)

L’algorithme donne en sortie la valeur 1 (la dernière valeur rentrée dans la case n).

Quelle valeur  obtient-on en sortie, en entrant la valeur -1 ?

la variable n reçoit d’abord en entrée la valeur 3.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 9 (3 élevé au carré)

L’algorithme donne en sortie la valeur 9 (la dernière valeur rentrée dans la case n).

Quelle valeur  obtient-on en sortie, en entrant la valeur 5 ?

la variable n reçoit d’abord en entrée la valeur 5.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 25 (5 élevé au carré)

L’algorithme donne en sortie la valeur 25 (la dernière valeur rentrée dans la case n).

Quelle valeur  obtient-on en sortie, en entrant la valeur 10 ?

la variable n reçoit d’abord en entrée la valeur 10.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 100 (10 élevé au carré)

L’algorithme donne en sortie la valeur 100 (la dernière valeur rentrée dans la case n).

Quelle valeur  obtient-on en sortie, en entrant la valeur 100 ?

la variable n reçoit d’abord en entrée la valeur 100.

Ensuite  après le bloc n=n**2, la variable n reçoit la valeur 10000 (100 élevé au carré)

L’algorithme donne en sortie la valeur 10000 (la dernière valeur rentrée dans la case n).

Cet algorithme calcule le carré du nombre entré.

Qu’obtient-on en sortie si on tape plgd(-4,3) dans la console ?

Comme -4>3 est faux on effectue l’instruction située après else et l’algorithme affiche 3 en sortie.

Qu’obtient-on en sortie si on tape plgd(-2,-3) dans la console ?

Comme -2>-3 est vrai on effectue l’instruction située après if et l’algorithme affiche -2 en sortie.

Qu’obtient-on en sortie si on tape plgd(\sqrt{2},1.42) dans la console ?

Comme \sqrt{2}>1.42 est faux on effectue l’instruction située après else et l’algorithme affiche 1.42 en sortie.

Qu’obtient-on en sortie si on tape plgd(3/7,5/13) dans la console ?

Comme 3/7>5/13 est vrai on effectue l’instruction située après if et l’algorithme affiche 0.42857142857142855 en sortie.

Cet algorithme affiche le plus grand des deux nombres proposés.

Pour k=0, on réalise le bloc d’instructions à savoir : on affecte à n un nombre pris au hasard entre 1 et 6, et on affiche en sortie ce nombre car le print(n) fait partie du bloc d’instructions (print(n) est aligné avec n=randint(1,6)).

Pour k=1, on réalise le bloc d’instructions à savoir : on affecte à n un nombre pris au hasard entre 1 et 6 ( ce nouveau nombre chasse le précédent de la case n), et on affiche en sortie ce nombre car le print(n) fait partie du bloc d’instructions (print(n) est aligné avec n=randint(1,6)).

…Pour k=19, on réalise le bloc d’instructions à savoir : on affecte à n un nombre pris au hasard entre 1 et 6 ( ce nouveau nombre chasse le précédent de la case n) , et on affiche en sortie ce nombre car le print(n) fait partie du bloc d’instructions (print(n) est aligné avec n=randint(1,6)).

Un exemple de résultat est :

1  2  1  2  3  6  6  6  6  5  4  4  1 3  3  4  4  5  6  5  6

Cet algorithme modèlise l’expérience de probabilité suivante :

on jette un dé à six faces vingt fois de suite.

La valeur initiale que l’on a entré dans la case mémoire c est 0.

pour i=1, on effectue le bloc d’instructions et c reçoit la valeur 0+50 c’est-à-dire 50.( cette valeur 50 chasse la précédente : 0).

pour i=2, on effectue le bloc d’instructions et c reçoit la valeur 50+50 c’est-à-dire 100. ( cette valeur 100 chasse la précédente : 50).

…

la boucle for i in range (1,b+1): signifie que i prend les valeurs 1,2,3,4,5,6 et 7(les valeurs sont strictement plus petites que b+1=7+1=8).

pour i=7, on effectue le bloc d’instructions et c reçoit la valeur 300+50 c’est-à-dire 350. ( cette valeur 350 chasse la précédente : 300). 

L’algorithme affiche en sortie la valeur 350 ( le print c est aligné avec le for… , donc il ne fait pas partie du bloc d’instructions de la boucle et sera réalisé quand la boucle sera achevée au moment où la dernière valeur rentrée dans c sera 350)

Cet algorithme calcule le produit a\times b en procédant ainsi: a+a+a+a+…+a\\\hspace{8.3cm}b fois

Avant de se lancer dans la programmation, il faut modéliser la situation.

Compte-tenu du modèle proposé, mieux vaut utiliser une boucle avec un bloc d’instructions qui recalcule le nombre de poignées de mains.

Dans le programme ci-dessous, c désigne le nombre de poignées de mains , n désigne le nombre total de personnes et i désigne le nombre intermédiaire de personnes. Ce n’est qu’à partir de i=3 personnes que les choses deviennent sérieuses.

Augmenter de 2% revient à multiplier par 1.02.

Si on note i, l’année et c le capital correspondant. On obtient le tableau de valeurs suivant:

L’idée est de créer un programme qui calcule le nouveau capital tant que celui-ci reste plus petit que 3500 euros et qui détermine la nouvelle année à chaque fois.

C’est en 2028 que le capital sera supérieur à 3500 euros.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.