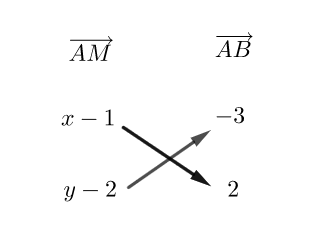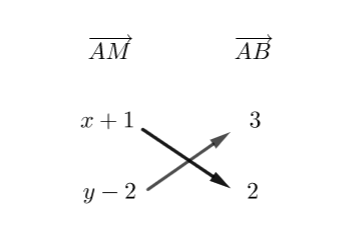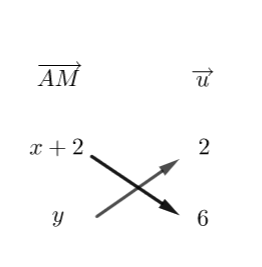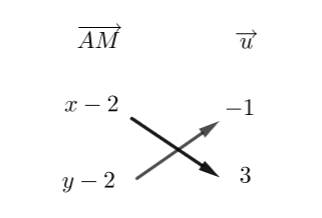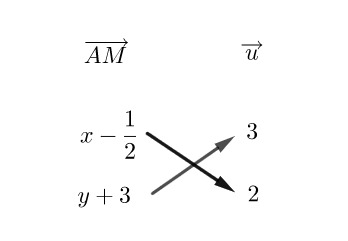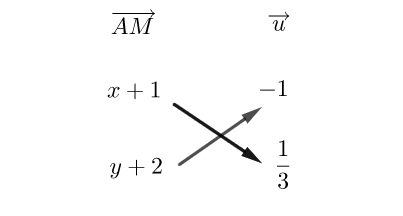sommaire
Vidéo
Exercice n°1
Soient A(1;2) et B(-2;4) deux points du plan.
On se propose de déterminer une équation cartésienne de la droite (AB) .
1. Calculer les coordonnées de \overrightarrow{AB}.
2. On note (x;y) les coordonnées d’un point M quelconque de la droite (AB).
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
3. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{AB} en fonction de (x;y).
4. En déduire une équation cartésienne de la droite (AB).
Vérification avec Géogébra.
Placer les points A et B dans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°2
Soient A(-1;2) et B(2;4) deux points du plan.
On se propose de déterminer une équation cartésienne de la droite (AB) .
1. Calculer les coordonnées de \overrightarrow{AB}.
2. On note (x;y) les coordonnées d’un point M quelconque de la droite (AB).
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
3. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{AB} en fonction de (x;y).
4. En déduire une équation cartésienne de la droite (AB).
Vérification avec Géogébra.
Placer les points A et B dans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°3
Soient A(-2;0) un point du plan et \overrightarrow{u}(2;6) un vecteur.
On se propose de déterminer une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
1. On note (x;y) les coordonnées d’un point M quelconque de la droite passant par A et de vecteur directeur \overrightarrow{u} .
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
2. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{u} en fonction de (x;y).
3. En déduire une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
Vérification avec Géogébra.
Placer le point A et construire le vecteur \overrightarrow{u} à partir de Adans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°4
Soient A(2;2) un point du plan et \overrightarrow{u}(-1;3) un vecteur.
On se propose de déterminer une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
1. On note (x;y) les coordonnées d’un point M quelconque de la droite passant par A et de vecteur directeur \overrightarrow{u} .
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
2. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{u} en fonction de (x;y).
3. En déduire une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
Vérification avec Géogébra.
Placer le point A et construire le vecteur \overrightarrow{u} à partir de Adans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°5
Soient A(\frac{1}{2};-3) un point du plan et D une droite d’équation 2x-3y+2=0 .
On se propose de déterminer, par le calcul, une équation cartésienne de la droite parallèle à D passant par A.
1. Déterminer les coordonnées d’un vecteur directeur de la droite D que l’on notera \overrightarrow{u}.
2. On note (x;y) les coordonnées d’un point M quelconque de la droite passant par A et parallèle à D .
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
3. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{u} en fonction de (x;y).
4. En déduire une équation cartésienne de la droite passant par A et parallèle à D.
Vérification avec Géogébra.
Placer le point A et saisir l’équation cartésienne de D 2x-3y+2=0 dans la colonne algèbre à gauche . Tracer la droite parallèle à D passant par A et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°6
Soient A(-1;-2) un point du plan et D une droite d’équation \frac{1}{3}x+y-2=0 .
On se propose de déterminer, par le calcul, une équation cartésienne de la droite parallèle à D passant par A.
1. Déterminer les coordonnées d’un vecteur directeur de la droite D que l’on notera \overrightarrow{u}.
2. On note (x;y) les coordonnées d’un point M quelconque de la droite passant par A et parallèle à D .
Exprimer les coordonnées de \overrightarrow{AM} en fonction de (x;y).
3. Exprimer le déterminant des vecteurs \overrightarrow{AM} et \overrightarrow{u} en fonction de (x;y).
4. En déduire une équation cartésienne de la droite passant par A et parallèle à D.
Vérification avec Géogébra.
Placer le point A(-1;-2) et saisir l’équation cartésienne de D \frac{1}{3}x+y-2=0 dans la colonne algèbre à gauche . Tracer la droite parallèle à D passant par A et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°7
Soient A(0;1) et B(3;3) deux points du plan.
On se propose de déterminer une équation cartésienne de la droite (AB) .
1. Calculer les coordonnées de \overrightarrow{AB}.
2. En déduire qu’une équation cartésienne de la droite (AB) est de la forme 2x-3y+c=0.
3. En utilisant le fait que le point A appartient à la droite (AB) , déterminer c et déterminer alors une équation cartésienne de la droite (AB) .
Vérification avec Géogébra.
Placer les points A et B dans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°8
Soient A(-\frac{2}{3};2) et B(\frac{1}{5};-1) deux points du plan.
On se propose de déterminer une équation cartésienne de la droite (AB) .
1. Calculer les coordonnées de \overrightarrow{AB}.
2. En déduire qu’une équation cartésienne de la droite (AB) est de la forme -3x-\frac{13}{15}y+c=0.
3. En utilisant le fait que le point A appartient à la droite (AB) , déterminer c et déterminer alors une équation cartésienne de la droite (AB) .
Vérification avec Géogébra.
Placer les points A et B dans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°9
Soient A(-1;1) un point du plan et \overrightarrow{u}(-3;5) un vecteur.
On se propose de déterminer une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
1. Justifier qu’une équation cartésienne de cette droite est de la forme 5x+3y+c=0.
2. En utilisant le fait que le point A appartient à cette droite , déterminer c et déterminer alors une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}. .
Vérification avec Géogébra.
Placer le point A et construire le vecteur \overrightarrow{u} à partir de Adans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°10
Soient A(2;5) un point du plan et \overrightarrow{u}(1;-\frac{2}{7}) un vecteur.
On se propose de déterminer une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}.
1. Justifier qu’une équation cartésienne de cette droite est de la forme -\frac{2}{7}x-y+c=0.
2. En utilisant le fait que le point A appartient à cette droite, déterminer c et déterminer alors une équation cartésienne de la droite passant par A et de vecteur directeur \overrightarrow{u}. .
Vérification avec Géogébra.
Placer le point A et construire le vecteur \overrightarrow{u} à partir de Adans le repère. Tracer la droite (AB) et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°11
Soient A(-1;-2) un point du plan et D une droite d’équation \frac{1}{3}x+y-2=0 .
On se propose de déterminer, par le calcul, une équation cartésienne de la droite parallèle à D passant par A.
1. Justifier qu’une équation cartésienne de cette droite est de la forme \frac{1}{3}x+y+c=0.
2. En utilisant le fait que le point A appartient à cette droite, déterminer c et déterminer alors une équation cartésienne de la droite passant par A et parallèle à D. .
Vérification avec Géogébra.
Placer le point A(-1;-2) et saisir l’équation cartésienne de D \frac{1}{3}x+y-2=0 dans la colonne algèbre à gauche . Tracer la droite parallèle à D passant par A et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.
Exercice n°12
Soient A(0;4) un point du plan et D une droite d’équation x+2y-1=0 .
On se propose de déterminer, par le calcul, une équation cartésienne de la droite parallèle à D passant par A.
1. Justifier qu’une équation cartésienne de cette droite est de la forme x+2y+c=0.
2. En utilisant le fait que le point A appartient à cette droite, déterminer c et déterminer alors une équation cartésienne de la droite passant par A et parallèle à D. .
Vérification avec Géogébra.
Placer le point A(0;4) et saisir l’équation cartésienne de D x+2y-1=0 dans la colonne algèbre à gauche . Tracer la droite parallèle à D passant par A et lire son équation dans la colonne Algèbre (celle de gauche) .
Remarque : comme il y a plusieurs équations cartésiennes, celle de Géogébra ne sera peut-être pas la même. Il suffira de multiplier ou diviser tous les coefficients par un même nombre pour s’apercevoir qu’il s’agit de la même droite.