Sommaire
Proportion, pourcentage d’une sous-population ( la partie) dans une population (le tout).
Pour les exercices sur les proportions qu’il faudra traiter, le plus simple sera de remplir le tableau ci-dessous. En effet, pour y parvenir il faudra répondre aux bonnes questions :
Quelle est la partie ? Quel est le tout ? Que connait-on ? Que cherche-t-on ?

Exemple n°1
Dans une classe de seconde comprenant 30 élèves, 40\% d’entre eux sont des filles.
Combien y’a-t-il de filles dans la classe ?
La partie : les filles de la classe.
Le tout : les élèves de la classe.
On connaît l’effectif du tout : 30 et le pourcentage de la partie : 40.
On cherche l’effectif de la partie.
On complète le tableau :

On effectue le calcul :\frac{30\times40}{100}=12.
On répond : il y a 12 filles dans la classe.
Exemple n°2
Une infime minorité des licenciés en football sont des femmes : 160 000 joueuses seulement, sur un total de 2,2 millions de personnes, selon la Fédération française en 2018.
Quel est le pourcentage de femmes licenciées parmi les personnes licenciées en foot-ball en France en 2018 ?
La partie : les femmes licenciées en foot-ball en France en 2018.
Le tout : les licenciés en foot-ball en France en 2018.
On connaît l’effectif du tout : 2200000 et l’effectif de la partie : 160000.
On cherche le pourcentage de la partie.
On complète le tableau :
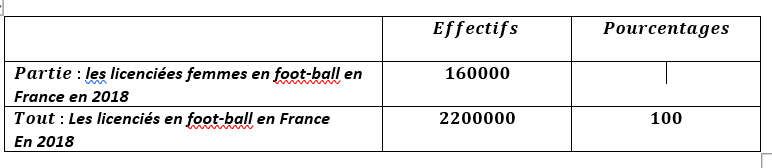
On effectue le calcul :\frac{160000\times100}{2200000}=7.2727.
On répond :le pourcentage des femmes parmi les licenciés en foot-ball en France en 2018 est 7.3\%.
Exercice n°1
Les résultats d’une enquête réalisée entre janvier et juillet 2018 auprès d’un échantillon représentatif de 9 074 personnes âgées de 18 ans à 75 ans résidant en France métropolitaine ont permis d’évaluer à 25,4 % le pourcentage de Français de 18 à 75 ans qui fument quotidiennement en 2018.
Combien y’a-t-il eu de personnes fumeurs interrogées pendant cette enquête ?
Exercice n°2
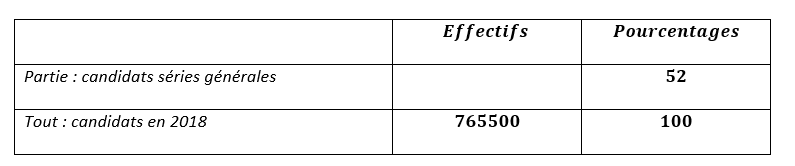
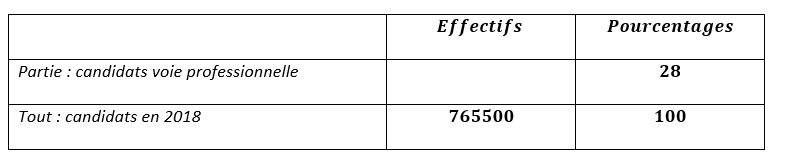
À la session de juin 2018, 765 500 candidats se sont présentés aux épreuves du baccalauréat, 52% dans les séries générales, 20% dans les séries technologiques, 28% dans la voie professionnelle.
- Combien y’avait-il de candidats en séries générales ?
2. Combien y’avait-il de candidats en séries technologiques ?
3. Combien y’avait-il de candidats dans la voie professionnelle ?
Exercice n°3
En 2018 , sur 398 060 candidats en séries générales le nombre de bacheliers généraux atteint 359 100 .
Calculer le pourcentage de réussite au bac en séries générales en 2018 en France.
Evolution
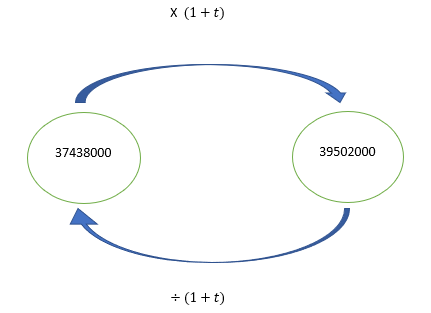
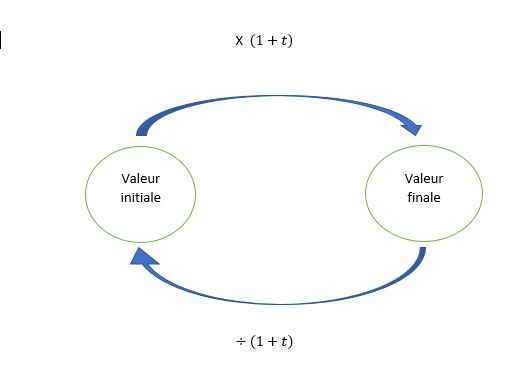
Pour les exercices sur les pourcentages d’évolution qu’il faudra traiter , on pourra remplir le schéma suivant.
Pour le faire, il faudra se poser les bonnes questions:
Quelle est la valeur initiale ? Quelle est la valeur finale ? Est-ce une augmentation ? Une diminution ? Que connaît-on ? Que cherche-t-on ?
Exemple n°3
D’un point de vue européen, un rapport de l’UEFA publié en 2017 confirme la croissance du football féminin dans toute l’Europe, à l’instar de la France. Ainsi, le nombre total de joueuses inscrites était de 1,365 million, contre 1,270 million en 2016.
Calculer le taux d’augmentation du nombre de joueuses de foot-ball en Europe entre 2016 et 2017.
La valeur initiale est 1270000. La valeur finale est 1365000. C’est une augmentation .On cherche t.
Méthode n°1: On complète le schéma.
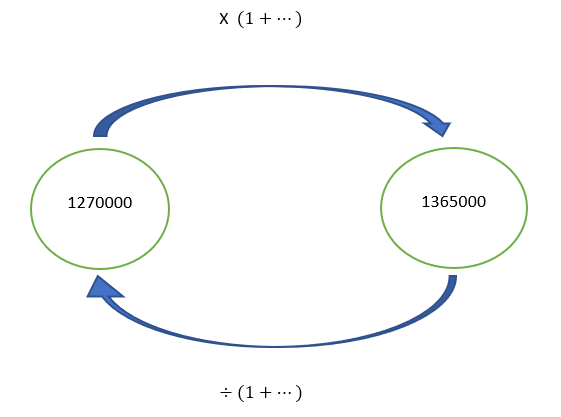
On note t le taux d’augmentation du nombre de joueuses de foot-ball en Europe entre 2016 et 2017.
On calcule \frac{1365000}{1270000}=1.07
On résout 1+t=1.07.
\hspace{1.8 cm}t=1.07-1
\hspace{1.8 cm}t=0.07
On exprime souvent t en pourcentage, la réponse devient : le nombre de joueuses de foot-ball en Europe entre 2016 et 2017 a augmenté de 7\%
Méthode n°2:
On applique la formule suivante t=\frac{V_{F}-V_{I}}{V_{I}}.
t=\frac{1365000-1270000}{1270000}=0.0748
le taux d’augmentation est 0.07.
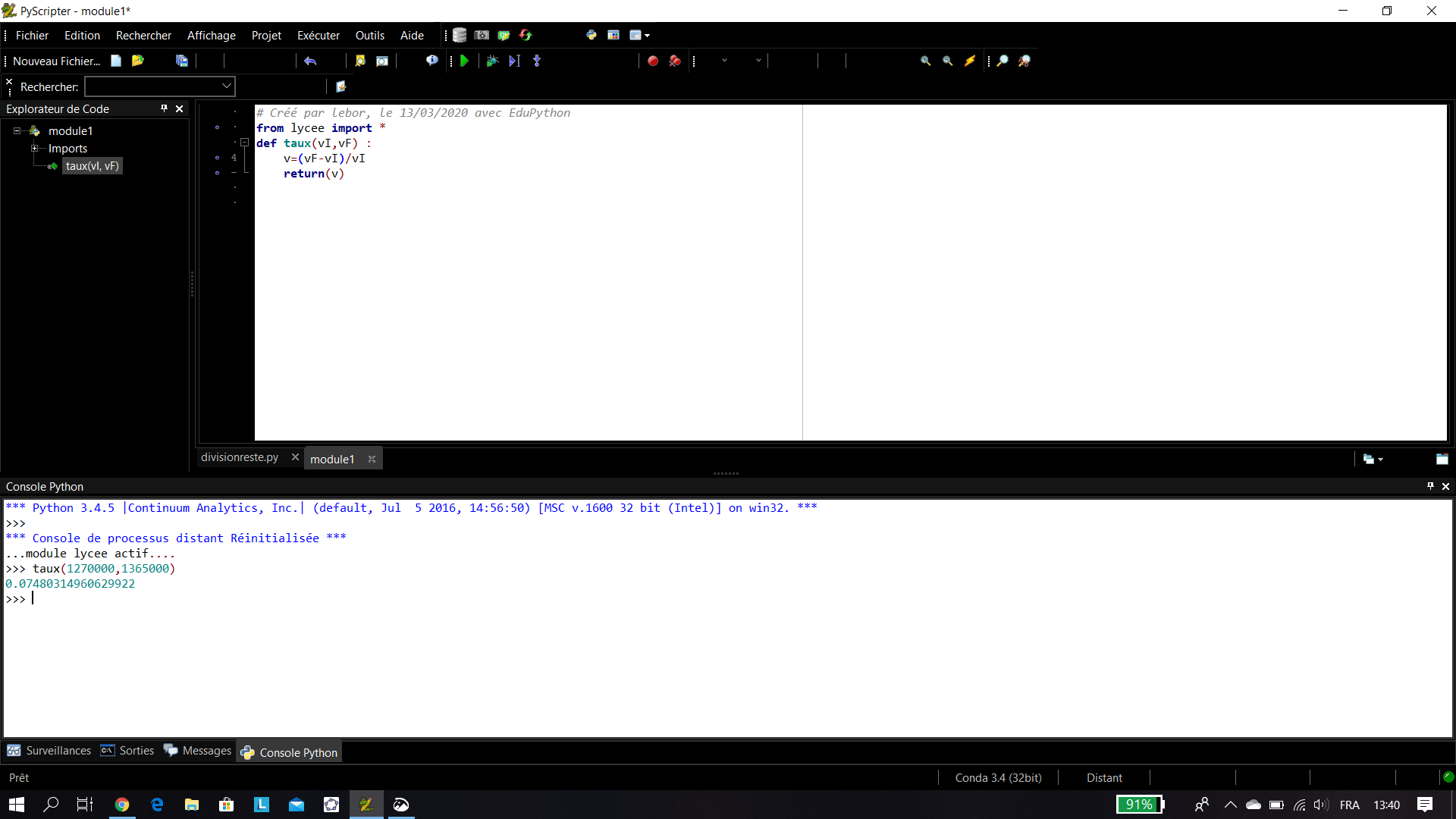
On peut créer une fonction en langage Python comme ci-après :
Exemple n°4
(extrait d’article de presse paru en Juin 2019)
Alors que le Mondial démarre vendredi en France, la région parisienne compte plus de 17 000 pratiquantes soit une progression de… 162 % par rapport à 2011.
Combien y’avait-il de pratiquantes en 2011 en région parisienne ?
La valeur finale est 17000 .C’est une augmentation de 162%. On cherche la valeur initiale.
On complète le schéma :
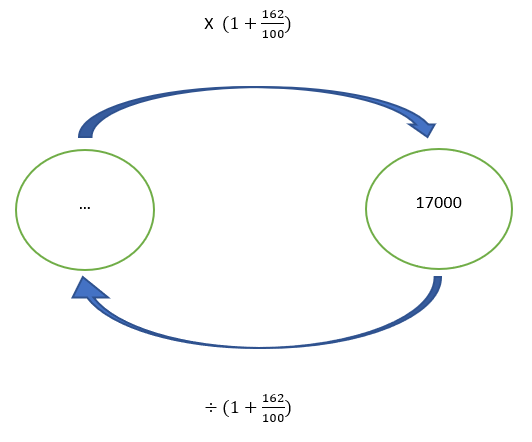
On calcule \frac{17000}{1+\frac{162}{100}}=\frac{17000}{1.162}=14629.95
Il y avait 14630 pratiquantes en 2011 en région parisienne.
Exemple n°5 : variation absolue, variation relative (ou taux d’évolution )
Voici un tableau où on a indiqué les populations de 4 pays en 2000 et 2018.
Compléter les 3 dernières colonnes.

Pour calculer la variation relative entre deux quantités V_{I} et V_{F} , on calcule V_{F}-V_{I} .
Pour calculer la variation absolue entre deux quantités V_{I} et V_{F} , on calcule \frac{V_{F}-V_{I}}{V_{I}} .
Les quantités V_{I} et V_{F} désignent valeur initiale (avant) et valeur finale (après);
Le plus simple pour compléter ce tableau est d’utiliser un tableur.

Dans la cellule D2 on saisit =C2-B2 puis on recopie vers le bas.
Dans la cellule E2 on saisit =D2/B2 puis on recopie vers le bas.
Dans la cellule F2 on saisit =E2*100 puis on recopie vers le bas.
Exemple n°6 : évolutions successives.
La population réunionnaise, avec ses 852 924 habitants (au 1er janvier 2016 selon l’INSEE), fait de la Réunion le DOM (Département d’Outre Mer) le plus peuplé et le 25 ème département le plus peuplé de France. Entre 2011 et 2016, la population augmente de +0,6% par an.
Combien y’avait-il d’habitants en 2011 ?
On peut illustrer la situation à l’aide du schéma ci-dessous.

Pour déterminer t le taux d’évolution global, on calcule 1.006^{5}=1.030 et on résout 1+t=1.030
d’où t=0.03
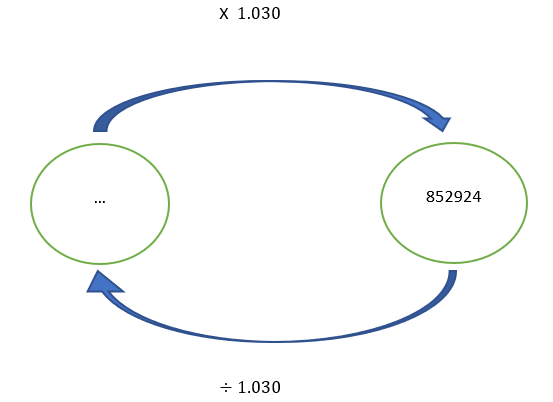
On calcule \frac{852924}{1.030}=828081.55
On répond : il y avait 828082 habitants à la réunion en 2011
Exemple n°7 : taux réciproque.
Un prix est augmenté de 25%, quelle réduction doit-on faire pour revenir au prix initial ?
Le plus simple est d’abord de schématiser la situation.
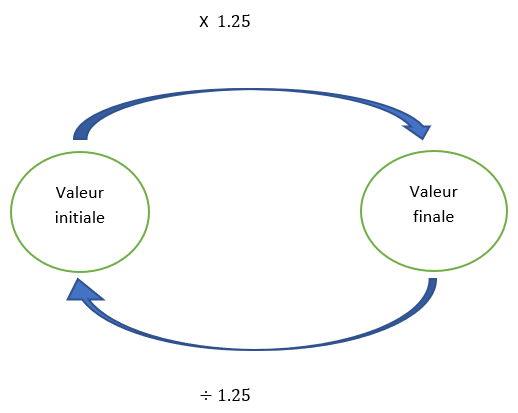
Pour passer du prix final au prix initial, il faut diviser par 1.25.
Diviser par 1.25 revient à multiplier par l’inverse de 1.25 c’est à dire \frac{1}{1.25}=0.8.
Il faudra multiplier le prix final par 0.8 pour retomber sur le prix de départ.
0.8=1-0.2Il faudra donc faire une réduction de 20\%
Exercice n°4
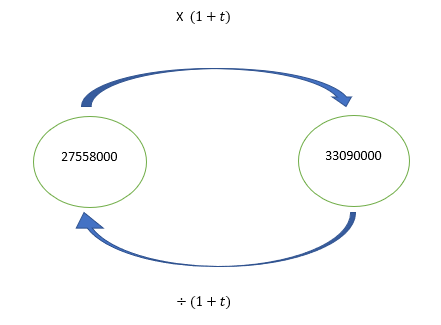
On s’intéresse à l’évolution du parc automobile français.

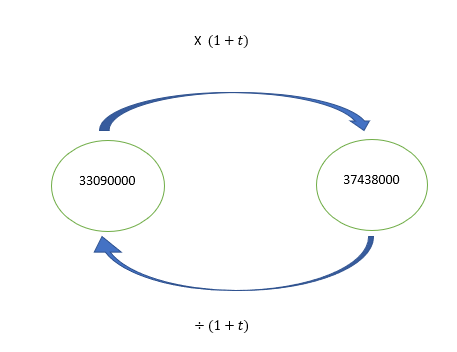
- Calculer le taux d’évolution du nombre de véhicules entre 1990 et 2000.
2. Calculer le taux d’évolution du nombre de véhicules entre 2000 et 2010.
3. Calculer le taux d’évolution du nombre de véhicules entre 2010 et 2018.
Exercice n°5 : extrait d’un article de Biosphère
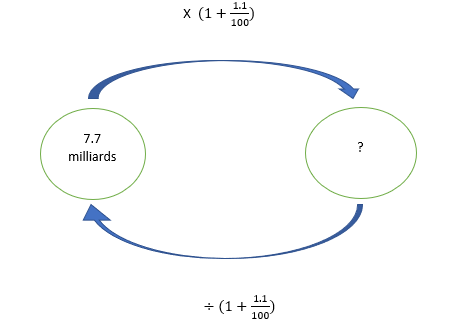
» La population mondiale au 1er janvier 2020. La Terre héberge environ 7,7 milliards d’habitants en ce 1er janvier 2020. Le taux de croissance annuel (+,1,1 %) reste élevé au regard de l’Histoire . »
- A l’aide de l’extrait ci-dessus, estimer la population mondiale en 2021.
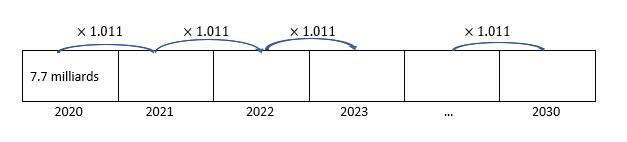
2. A l’aide de l’extrait ci-dessus, estimer la population mondiale en 2030.
Exercice n°6
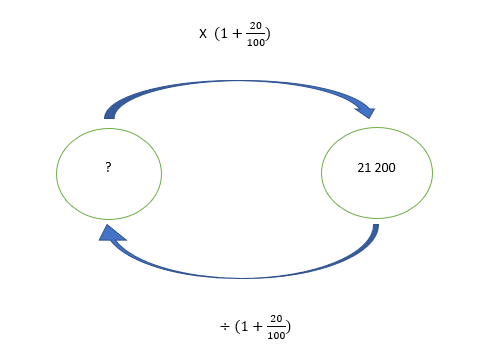
Pour l’achat d’une voiture, la TVA est de 20%.
Si le prix affiché en magasin d’une voiture est : 21 200 euros, quel est le prix HT ( hors taxe) de cette voiture ?