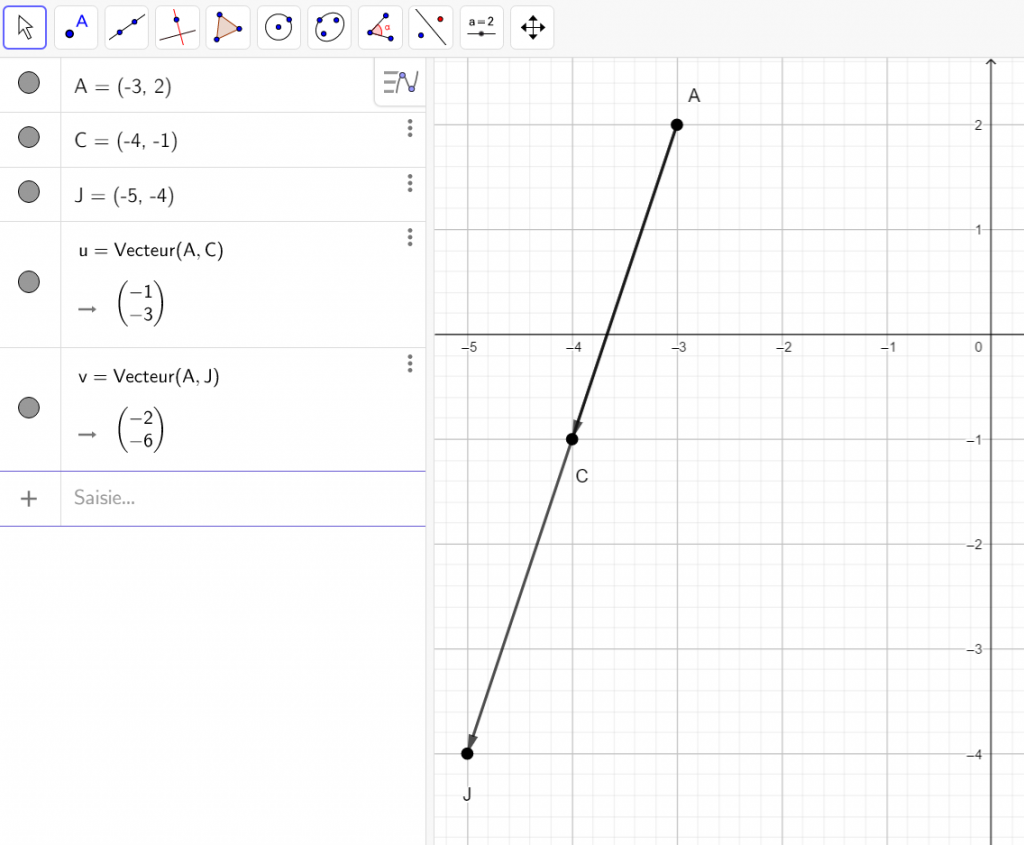
Soient deux points A(-3;2) et C(-4;-1). On veut déterminer les coordonnées du point J tel que \overrightarrow{AJ}=2\overrightarrow{AC}.
Comme on le les connaît pas, on les appelle x et y.
On pose J(x;y).
Les vecteurs \overrightarrow{AJ} et 2\overrightarrow{AC} sont égaux donc leurs coordonnées sont égales.
Tâche n°1 : Je calcule les coordonnées de \overrightarrow{AJ} . Puis je calcule les coordonnées de \overrightarrow{AC} et ensuite de 2\overrightarrow{AC}.
Pour déterminer les coordonnées du vecteur \overrightarrow{AJ}.
Je repère les coordonnées des points A et J.
\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{0.4cm}x_{J}\hspace{0.2cm}y_{J}\\\hspace{1.8cm}A(-3;2)\hspace{0.2cm}J(x;y)J’écris la formule : \overrightarrow{AJ}(x_{J}-x_{A};y_{J}-y_{A})
On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.
\overrightarrow{AJ}(x-(-3);y-2)\\\overrightarrow{AJ}(x+3;y-2)Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.
Je repère les coordonnées des points A et C.
\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{0.6cm}x_{C}\hspace{0.2cm}y_{C}\\\hspace{1.8cm}A(-3;2)\hspace{0.2cm}C(-4;-1)J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})
On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.
\overrightarrow{AC}((-4)-(-3);(-1)-2)\\\overrightarrow{AC}(-4+3;-3)\\\overrightarrow{AC}(-1;-3)Pour obtenir les coordonnées du vecteur 2\overrightarrow{AC}, je dois multiplier le coordonnées du vecteur \overrightarrow{AC} par 2\\2\overrightarrow{AC}({2}\times{(-1)};{2}\times{(-3)})\\2\overrightarrow{AC}(-2;-6)
Tâche n°2 : J’écris que les coordonnées de \overrightarrow{AJ}et de 2\overrightarrow{AC}sont égales pour obtenir deux équations du premier degré.
L’abscisse de \overrightarrow{AJ}=l’abscisse de 2\overrightarrow{AC}\\x+3=-2\\3 n’est pas à sa place à gauche, j’enlève 3 de chaque côté.
x=-2-3\\x=-5L’ordonnée de \overrightarrow{AJ}=l’ordonnée de 2\overrightarrow{AC}\\y-2=-6\\-2 n’est pas à sa place à gauche, j’ajoute 2 de chaque côté.
y=-6+2\\y=-4Donc J(-5;-4)