Le triangle ABC ci-dessous est rectangle en A.
De plus AB=18 et AC=8.
On place les points D et E respectivement sur les segments [AC] et [AD] tels que AD=BE.
L’ objectif de ce problème est de déterminer la position du point D sur le segment [AC] pour que l’aire du triangle ADE soit égale à la moitié de l’aire du triangle ABC.
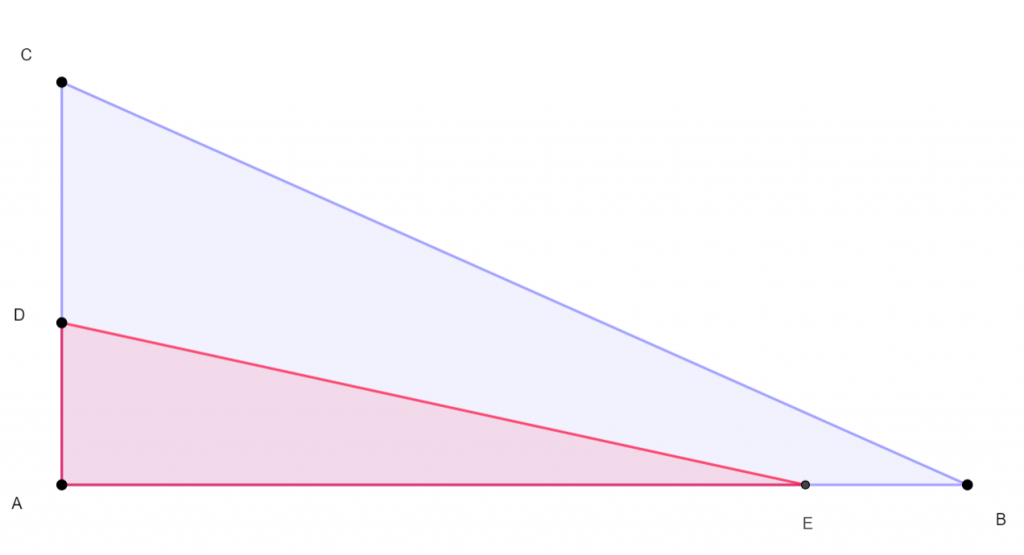
Résolution géométrique à l’aide du logiciel Géogébra.
1. Construction de la figure avec Géogébra.
2. Réponse au problème posé avec Géogébra.
Résolution par lecture graphique d’une courbe obtenue à l’aide du logiciel Géogébra.
Comme l’aire du triangle ADE dépend de la distance AD, on va chercher comment cette aire s’exprime en fonction de la distance.
Ensuite on déterminera par lecture graphique l’antécédent de 36 ( la moitié de l’aire de ABC qui vaut 72).
Résolution algébrique du problème.
On note x la distance AD.
- A quel intervalle appartient le nombre x ?
2. Exprimer, en fonction de x, l’aire du triangle ADE que l’on notera f(x).
3. Le but de cette question est de résoudre l’équation -\frac{1}{2}x^2+9x=36
a. Faire tout passer à gauche pour que 0 apparaisse à droite.
b. Mettre -\frac{1}{2} en facteur dans le membre de gauche.
c. Développer (x-9)^2 puis en déduire que x^2-18x=(x-9)^2-81.
d. En remplaçant x^2-18x par(x-9)^2-81, l’équation devient -\frac{1}{2}((x-9)^2-81+72)=0. Finir alors la résolution de la nouvelle équation.
4. Répondre au problème posé.



