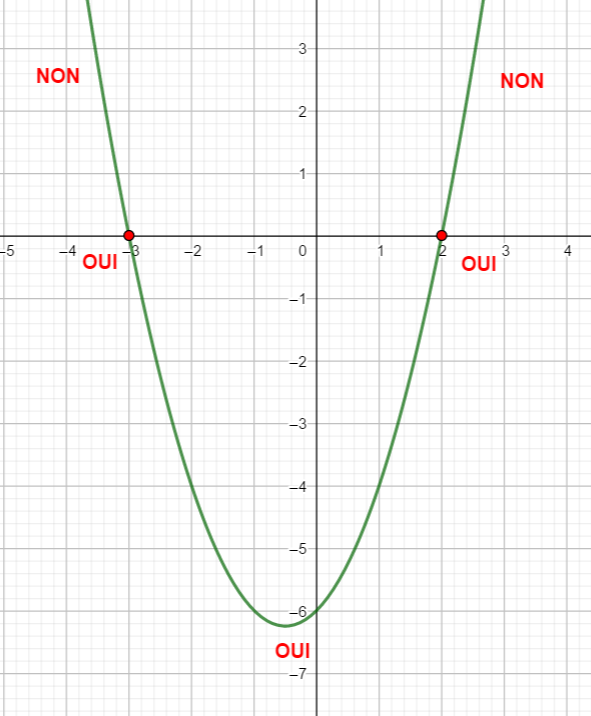
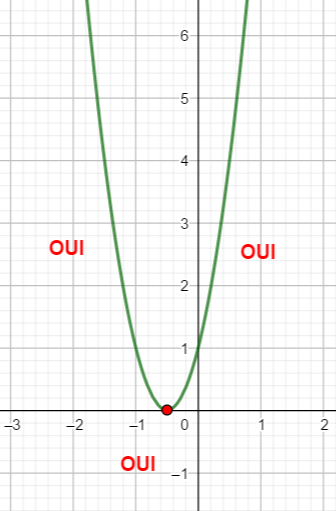
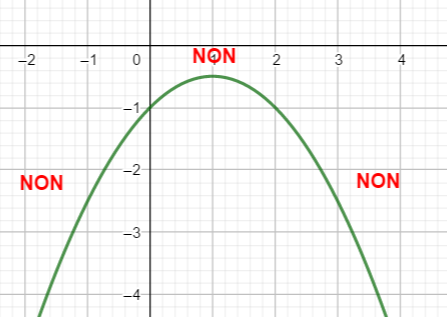
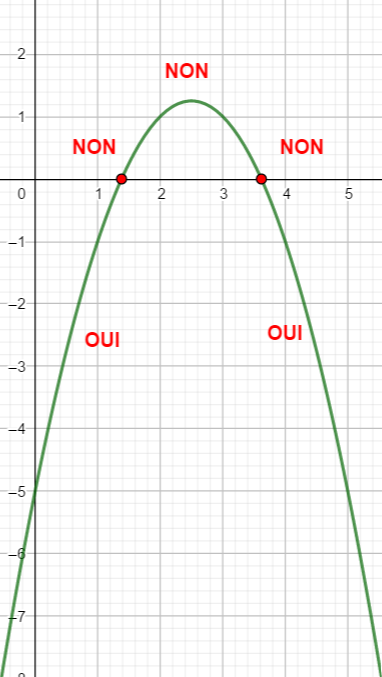
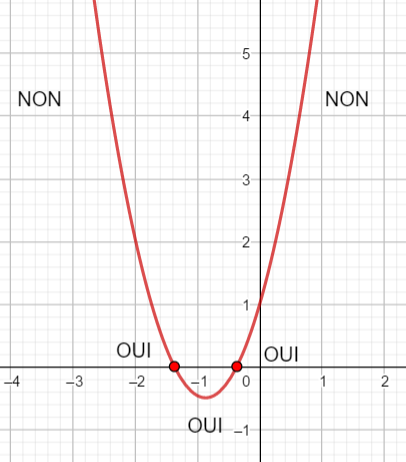
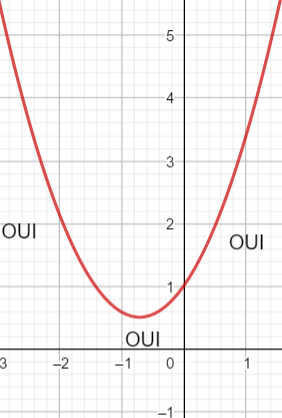
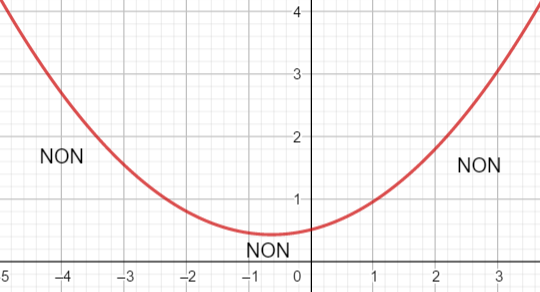
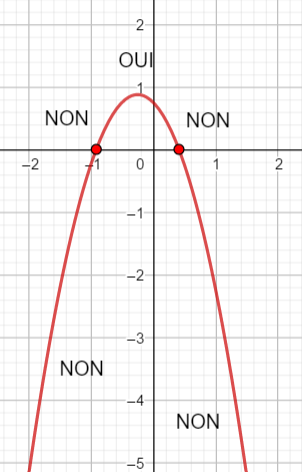
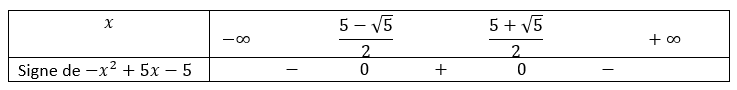Un petit conseil, avant de vous lancer dans le calcul de \Delta, faire une conjecture graphique en utilisant la fenêtre Géogébra ci-dessous . N’hésitez pas à déplacer le graphique et à uliliser Agrandissement et Réduction pour faire apparaître les points d’intersection éventuels.
Exercice :
En utilisant le théorème du cours résoudre les inéquations suivantes :
Pour valider votre réponse, utiliser la page Calcul Formel de Géogébra ci-dessous: