Sommaire
Aspect algébrique du nombre dérivé : la limite du taux de variation.
Activité d’approche avec la fonction carré
Le but de cette question est d’ exprimer en fonction de h, le coefficient de la droite (AM).
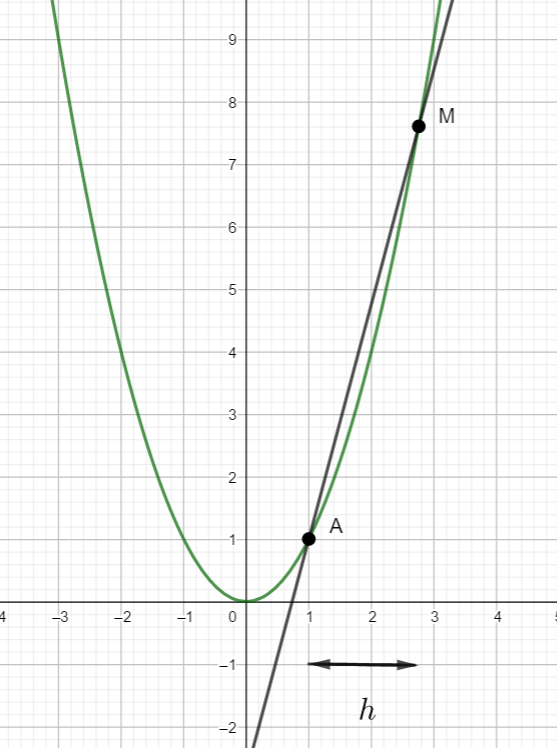
- Lire graphiquement les coordonnées du point A puis déterminer les coordonnées du point M en fonction de h. Aide : l’abscisse de M est 1+h .
2. Montrer que le coefficient directeur de la droite (AM) est égal à 2+h. On appelle aussi taux de variation la quantité obtenue.
3. Vers quelle valeur se rapproche le coefficient directeur de la droite (AM) quand les valeurs de h se rapprochent de 0 sans être égales à zéro ? On verra plus tard que cette valeur est notée f'(1).
Définition 1
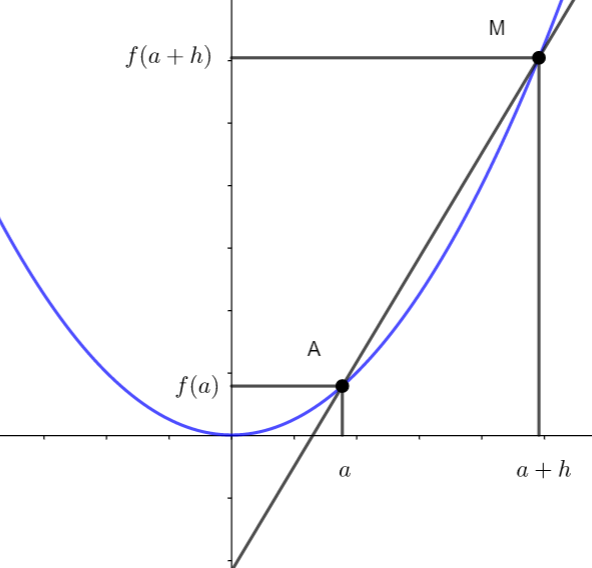
Le taux de variation de f entre a et a+h est le nombre
t(h)=\frac{f(a+h)-f(a)}{h}
Ce nombre est la pente de la droite (AM) sécante à la courbe passant par A et M.
Définition 2
Si le taux de variation t(h) tend vers un nombre réel quand h tend vers 0, on dit que la fonction f est dérivable en a. Ce nombre est appelé nombre dérivé en a et est noté f'(a). On écrit
f'(a)=lim_{h\to 0}\frac{f(a+h)-f(a)}{h}
Remarque : Nous avons établi , dans l’activité d’approche que le nombre dérivé en 1 pour la fonction carré est égal à 2
Exercice n°1 (démonstration au programme)
On se propose de déterminer le nombre f'(a) pour la fonction carré.
- Montrer que \frac{f(a+h)-f(a)}{h}=2a +h
2. Vers quelle valeur se rapproche 2a +h quand h se rapproche de 0 ? En déduire f'(a).
Synthèse de l’exercice n°1
La fonction carré définie sur \mathbf{R} par f(x)=x^2 admet pour fonction dérivée f'(x)=2x définie sur \mathbf{R}.
Exercice n°2 (démonstration au programme)
On se propose de déterminer le nombre f'(a) pour la fonction inverse.
- Montrer que \frac{f(a+h)-f(a)}{h}=-\frac{1}{a(a+h)}
2. Vers quelle valeur se rapproche -\frac{1}{a(a+h)} quand h se rapproche de 0 ? En déduire f'(a).
Synthèse de l’exercice n°2
La fonction inverse définie sur \mathbf{R}^* par f(x)=\frac{1}{x} admet pour fonction dérivée f'(x)=-\frac{1}{x^2} définie sur \mathbf{R}^* .
Exercice n°3 (démonstration hors programme)
On se propose de déterminer le nombre f'(a) pour la fonction cube.
- Montrer que (a+b)^3=a^3+3a^2b+3ab^2+b^3
2. Montrer que \frac{f(a+h)-f(a)}{h}=3a^2+3ah+h^2
3. Vers quelle valeur se rapproche 3a^2+3ah+h^2 quand h se rapproche de 0 ? En déduire f'(a).
Synthèse de l’exercice n°3
La fonction cube définie sur \mathbf{R} par f(x)=x^3 admet pour fonction dérivée f'(x)=3x^2 définie sur \mathbf{R}.
Aspect graphique du nombre dérivé : le coefficient directeur de la tangente à la courbe en un point.
Activité d’approche avec la fonction carré
De façon naïve la droite (AM) coupe la courbe en deux points A et M , on dit que c’est une sécante.
Toujours de façon naïve, quand la droite touche la courbe en seul point, on dit que c’est une tangente ( penser à la tangente à un cercle).
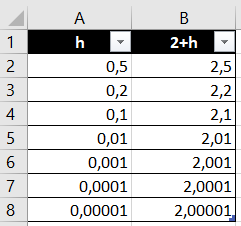
En utilisant la figure Géogébra ci-dessous, où est représentée la courbe de la fonction carré, déplacer le point M en le faisant se rapprocher de A. Observer les valeurs du coefficient directeur de la droite (AM) dans la colonne de gauche.
Lorsque M se déplace vers A, vers quelle valeur se rapprochent les valeurs du coefficient directeur de la droite (AM)?
Remarque : quand M est presque confondu avec A, la droite (AM) se rapproche de la tangente.
Définition 2
La tangente à la courbe de la fonction f au point A d’abscisse a est la droite passant par A et de pente f'(a).
Propriété
Si une fonction f est dérivable en a alors la tangente à la courbe en A(a;f(a)) a pour équation
y=f'(a)(x-a)+f(a).
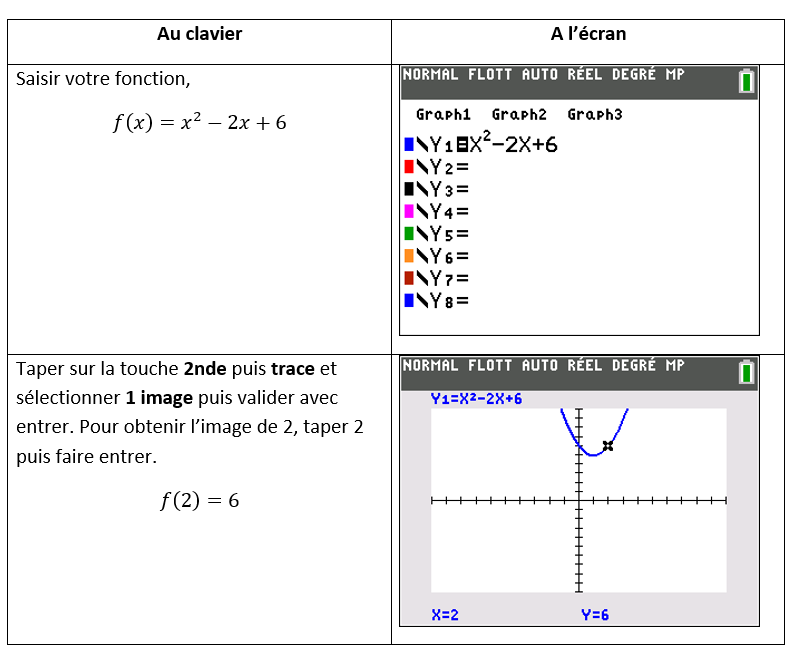
Pour déterminer l’image d’un nombre avec la calculatrice TI-83 Premium CE
Par exemple, déterminer f(2) avec la calculatrice TI-83 Premium CE quand f(x)=x^2-2x+6.
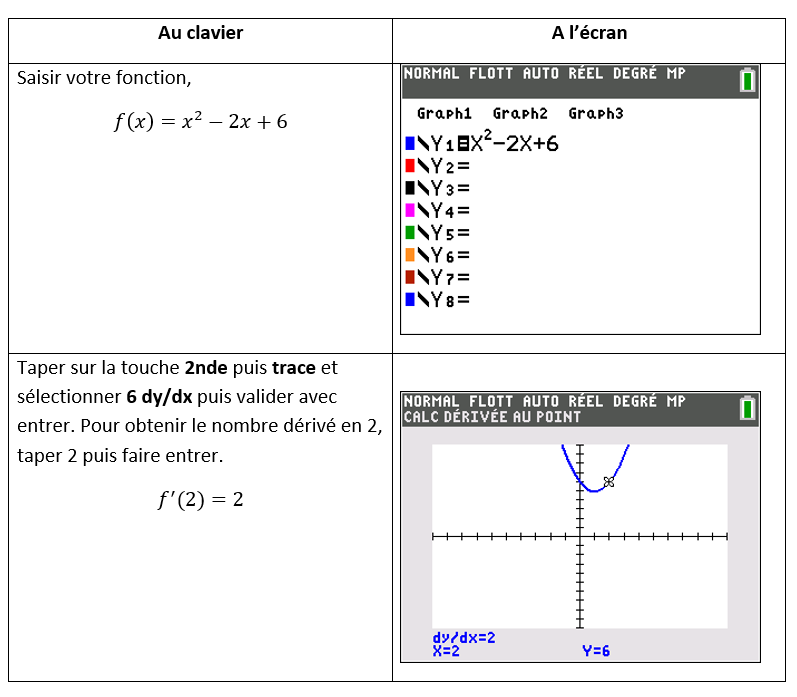
Pour déterminer un nombre dérivé avec la calculatrice TI-83 Premium CE
Par exemple, déterminer f'(2) avec la calculatrice TI-83 Premium CE quand f(x)=x^2-2x+6.
Exercice n°4
On se propose de déterminer l’équation réduite de la tangente à la courbe de la fonction carré au point d’abscisse
- Calculer f(1)
2. Calculer f'(1). Dans la synthèse de l’exercice n°1, on a établi que la fonction carré définie sur \mathbf{R} par f(x)=x^2 admet pour fonction dérivée f'(x)=2x définie sur \mathbf{R}.
3. En remplaçant f(1) et f'(1) par les valeurs trouvées dans les questions précédentes dans l’équation y=f'(a)(x-a)+f(a) , déterminer l’équation réduite de la tangente.
Exercice n°5
On se propose de déterminer l’équation réduite de la tangente à la courbe de la fonction inverse au point d’abscisse 2
- Calculer f(2)
2. Calculer f'(2). Dans la synthèse de l’exercice n°2, on a établi que la fonction inverse définie sur \mathbf{R}^* par f(x)=\frac{1}{x} admet pour fonction dérivée f'(x)=-\frac{1}{x^2} définie sur \mathbf{R}^* .
3. En remplaçant f(2) et f'(2) par les valeurs trouvées dans les questions précédentes dans l’équation y=f'(a)(x-a)+f(a) , déterminer l’équation réduite de la tangente.
Exercice n°6
On se propose de déterminer l’équation réduite de la tangente à la courbe de la fonction cube au point d’abscisse -1
- Calculer f(-1)
2. Calculer f'(-1). Dans la synthèse de l’exercice n°2, on a établi que la fonction cube définie sur \mathbf{R} par f(x)=x^3 admet pour fonction dérivée f'(x)=3x^2 définie sur \mathbf{R}.
3. En remplaçant f(-1) et f'(-1) par les valeurs trouvées dans les questions précédentes dans l’équation y=f'(a)(x-a)+f(a) , déterminer l’équation réduite de la tangente.
Valider avec Géogébra les résultats des exercices 4, 5 et 6.
Dans la colonne Algèbre située à gauche, saisir par exemple f(x)=x^2, la courbe apparaît dans le repère.
Placer le point A de la courbe d’abscisse 1. Pour cela cliquer sur le deuxième onglet en partant de la gauche et sélectionner Point sur Objet dans le menu déroulant. Cliquer ensuite au bon endroit sur la courbe pour obtenir le point A.
Pour tracer la tangente, cliquer sur le quatrième onglet en partant de la gauche et sélectionner Tangentes dans le menu déroulant. Cliquer ensuite sur le point A et sur la courbe. La tangente apparaît et son équation aussi dans la colonne de gauche.