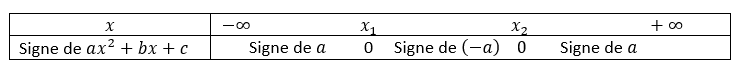Sommaire
Variations d’une fonction sur un intervalle
Activité d’approche
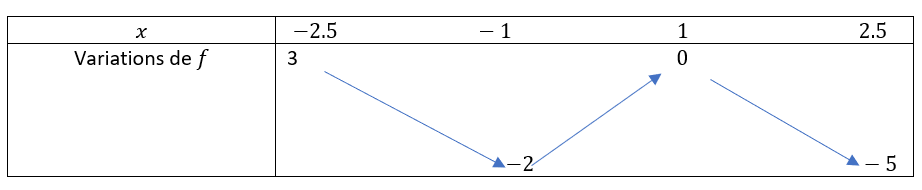
On a tracé la courbe d’une fonction définie sur l’intervalle [-2.5;2.5] dans le repère ci-dessous et on a créé un point A sur cette courbe.
Déplacer le point A de la gauche vers la droite en cliquant sur le premier onglet en partant de la gauche et en sélectionnant Déplacer dans le menu déroulant.
- Dresser ensuite le tableau de variations sur l’intervalle [-2.5;2.5] à l’aide du graphique.
Vous pourrez visionner la vidéo ci-dessous si besoin est.
Tracer la tangente à la courbe au point A en cliquant sur le quatrième onglet en partant de la gauche et en sélectionnant Tangentes dans le menu déroulant. Puis dans le repère cliquer sur la courbe et sur le point A. L’équation réduite de la tangente apparaît dans la colonne de gauche.
Déplacer le point A de la gauche vers la droite en cliquant sur le premier onglet en partant de la gauche et en sélectionnant Déplacer dans le menu déroulant. Et observer le signe du coefficient directeur de la tangente qui est le nombre dérivé.
2. Compléter alors le tableau de signes ci-dessous

Théorème 1
Soit f une fonction dérivable sur un intervalle I et f’ sa dérivée sur I.
Si f est croissante sur I alors pour tout réel x de l’intervalle I , on a f'(x)\geq 0 .
Si f est décroissante sur I alors pour tout réel x de l’intervalle I , on a f'(x)\leq 0 .
Théorème 2
Soit f une fonction dérivable sur un intervalle I et f’ sa dérivée sur I.
Si pour tout réel x de l’intervalle I , on a f'(x)\geq 0 alors f est croissante sur I .
Si pour tout réel x de l’intervalle I , on a f'(x)\leq 0 alors f est décroissante sur I .
Exercice n°1
AIDE : Dans cet exercice et les suivants, il faudra calculer f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.
De plus il faudra étudier le signe de f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.
Soit la fonction f définie sur [0;4] par f(x)=3x^2-12x+4.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [0;4].
3. Dresser le tableau de la fonction f sur l’intervalle [0;4].
Exercice n°2
Soit la fonction f définie sur [-4;4] par f(x)=x^3-12x.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [-4;4].
3. Dresser le tableau de la fonction f sur l’intervalle [-4;4].
Valider les variations avec Géogébra
On saisit par exemple
f(x)=3x^2-12x+4 dans la colonne de gauche et on lit graphiquement les variations de f sur [0;4] puis on compare avec le tableau de variations obtenu.
Si vous ne voyez pas la courbe dans son ensemble, utilisez le 11ème onglet pour déplacer le graphique, agrandir ou réduire.
Extremums d’une fonction ( c’est-à-dire maximum ou minimum)
Activité d’approche
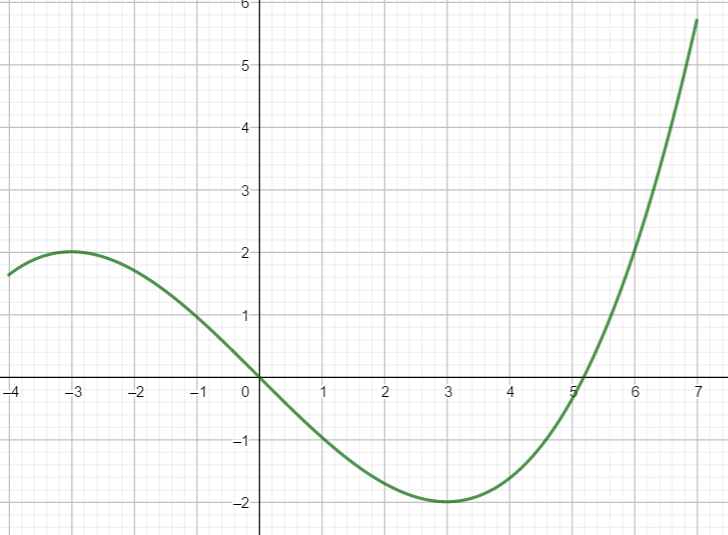
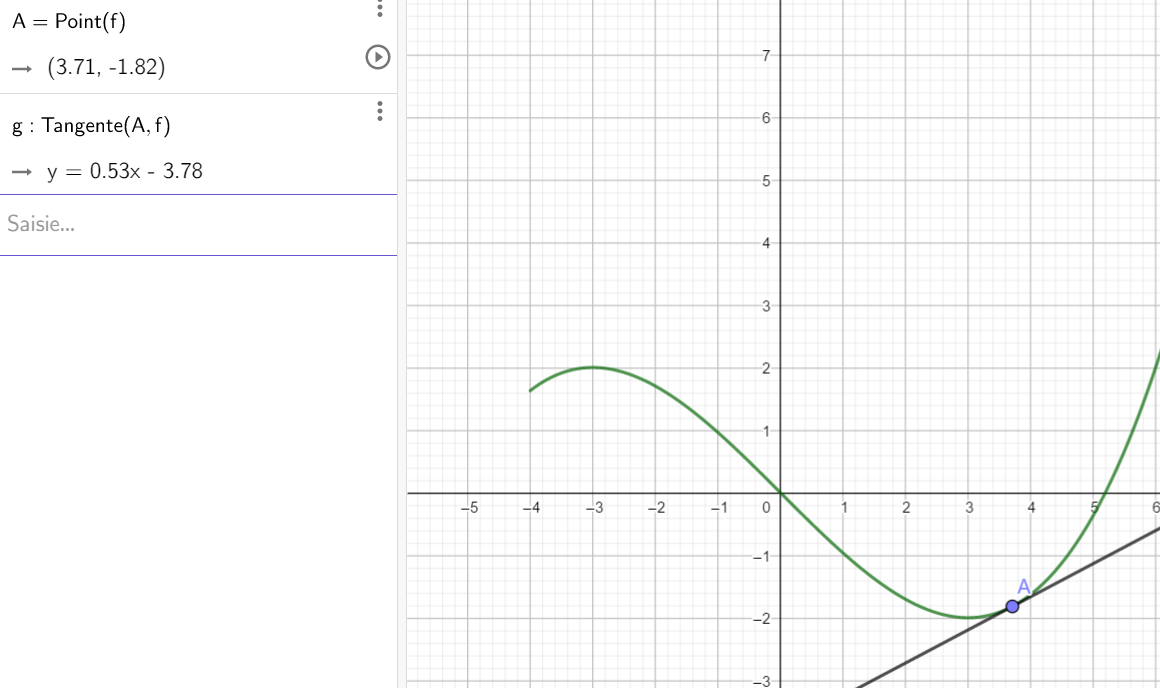
On a tracé la courbe d’une fonction définie sur l’intervalle [-4;7] dans le repère ci-dessous .
- Y’a-t-il un point situé plus bas que tous les autres ? Si oui compléter l’inégalité suivante f(x)\geq …
On peut déplacer le point A sur la figure ci-dessus et lire dans la colonne de gauche les coordonnées du point situé le plus bas. On peut aussi regarder les ordonnées du point A pour compléter les pointillés.
2. Y’a-t-il un point situé plus haut que tous les autres ? Si oui compléter l’inégalité suivante f(x)\leq …
On peut déplacer le point A sur la figure ci-dessus et lire dans la colonne de gauche les coordonnées du point situé le plus haut. On peut aussi regarder les ordonnées du point A pour compléter les pointillés.
Définitions
On considère une fonction f définie sur un intervalle I et \alpha et \beta deux réels de I.
f admet un maximum en \alpha signifie que pour tout x de I, f(x)\leq f(\alpha).
f admet un minimum en \beta signifie que pour tout x de I, f(x)\geq f(\beta).
Interprétation graphique : le point le plus haut de la courbe a pour coordonnées (\alpha;f(\alpha)) et le point le plus bas de la courbe a pour coordonnées (\beta;f(\beta))
Extremum local d’une fonction
Activité d’approche
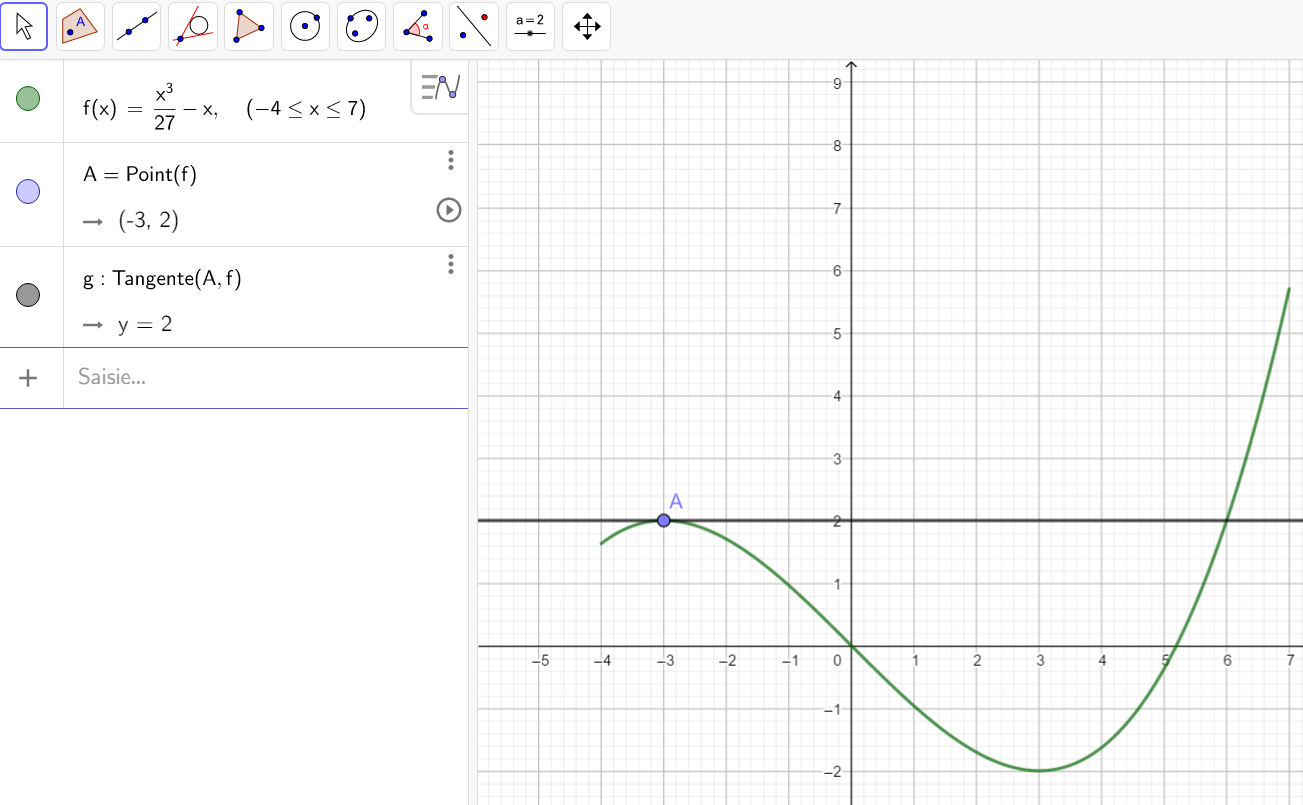
On reprend la courbe de l’activité précédente
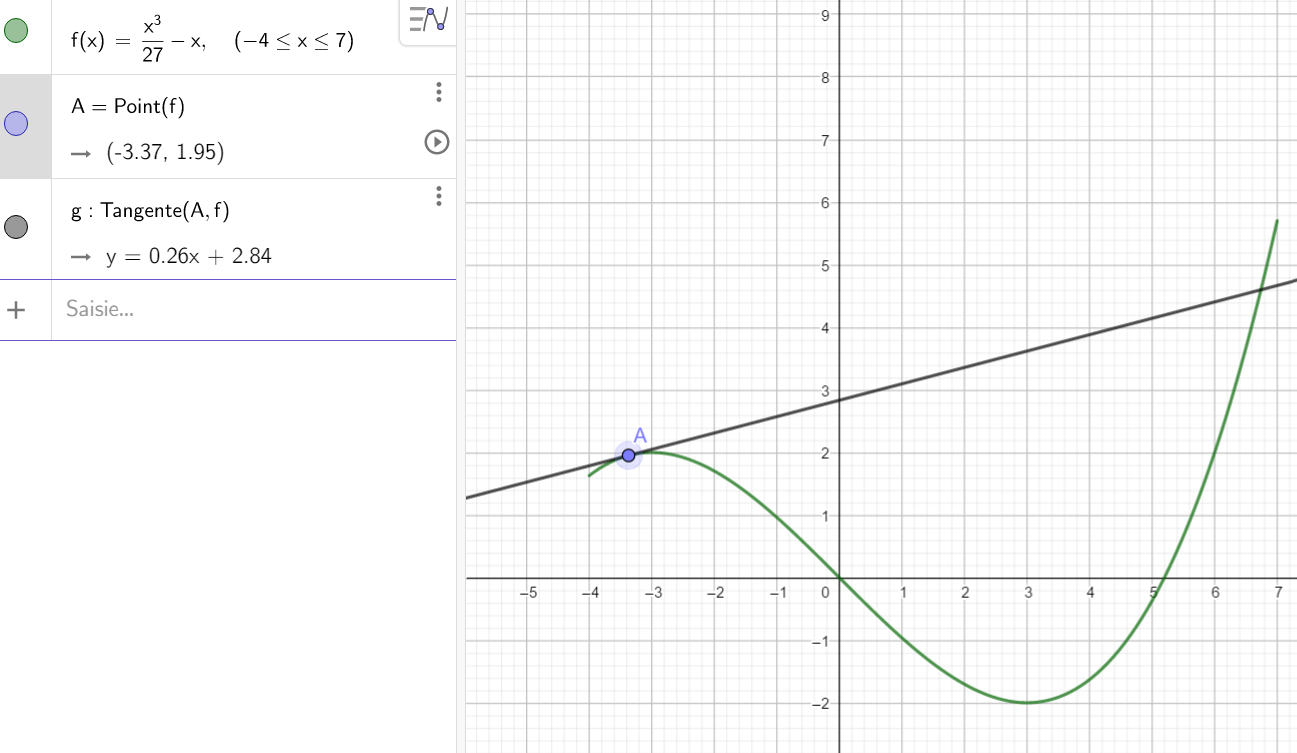
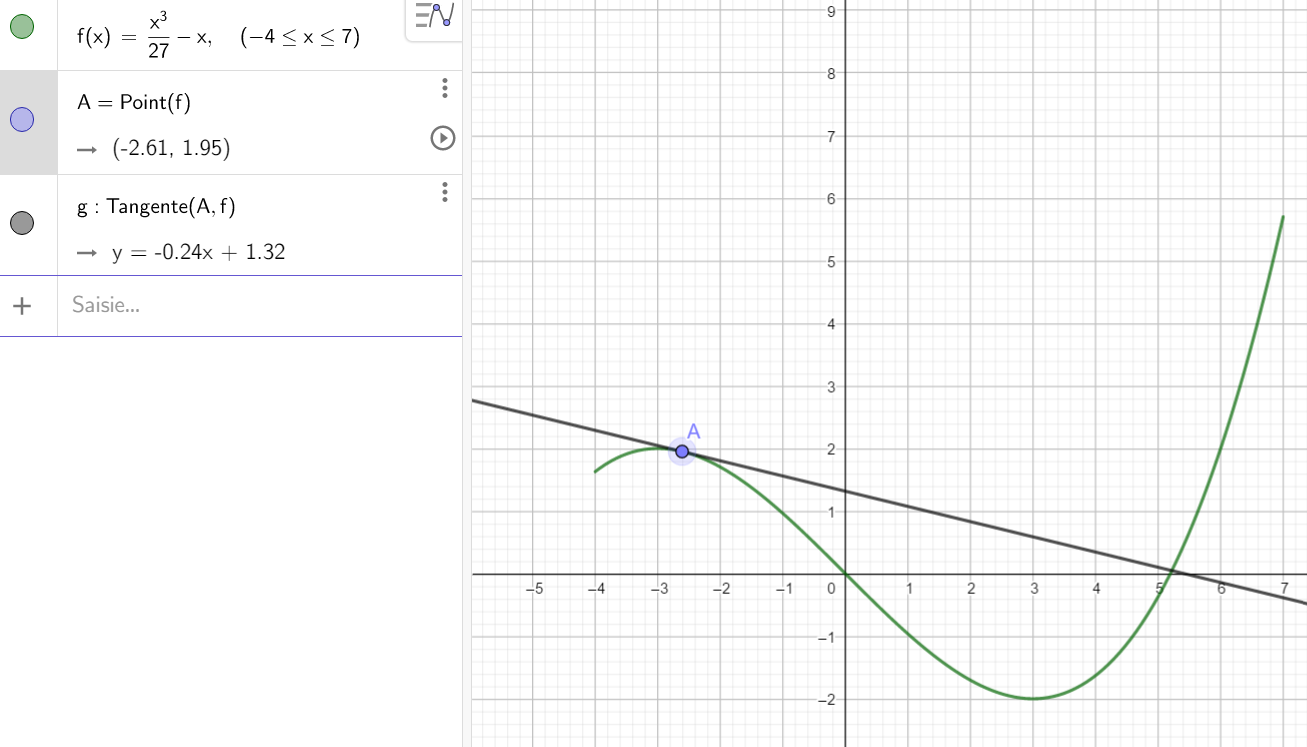
- a. Quelle est la valeur du maximum sur l’intervalle ouvert ]-3.5;-2.5[ ?
b. Déterminer graphiquement la valeur de f'(-3).
Tracer la tangente à la courbe au point A en cliquant sur le quatrième onglet en partant de la gauche et en sélectionnant Tangentes dans le menu déroulant. Puis dans le repère cliquer sur la courbe et sur le point A. L’équation réduite de la tangente apparaît dans la colonne de gauche.
Déplacer le point A de la gauche vers la droite en cliquant sur le premier onglet en partant de la gauche et en sélectionnant Déplacer dans le menu déroulant. Et observer la valeur du coefficient directeur de la tangente qui est le nombre dérivé au point de la courbe d’abscisse -3.
c. Quel est le signe de la dérivée pour les valeurs de x inférieures à -3 ? Quel est le signe de la dérivée pour les valeurs de x supérieures à -3?
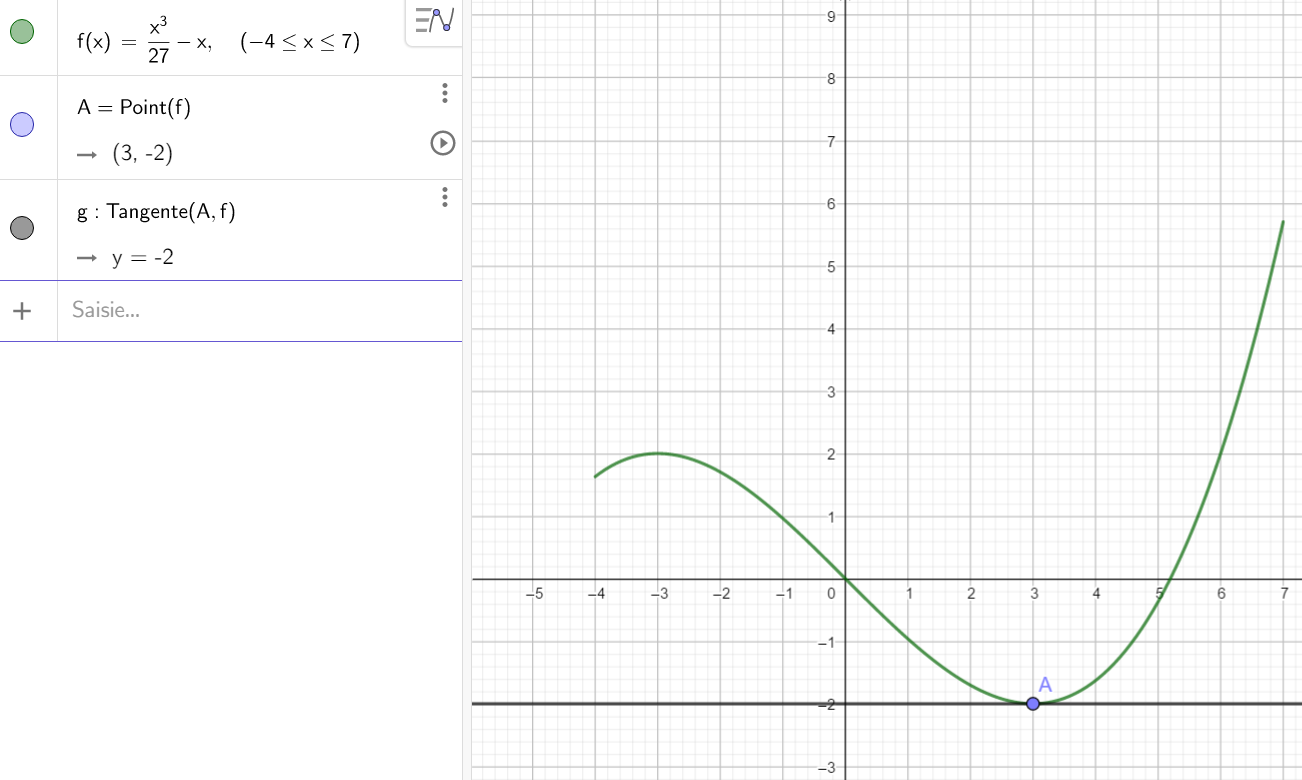
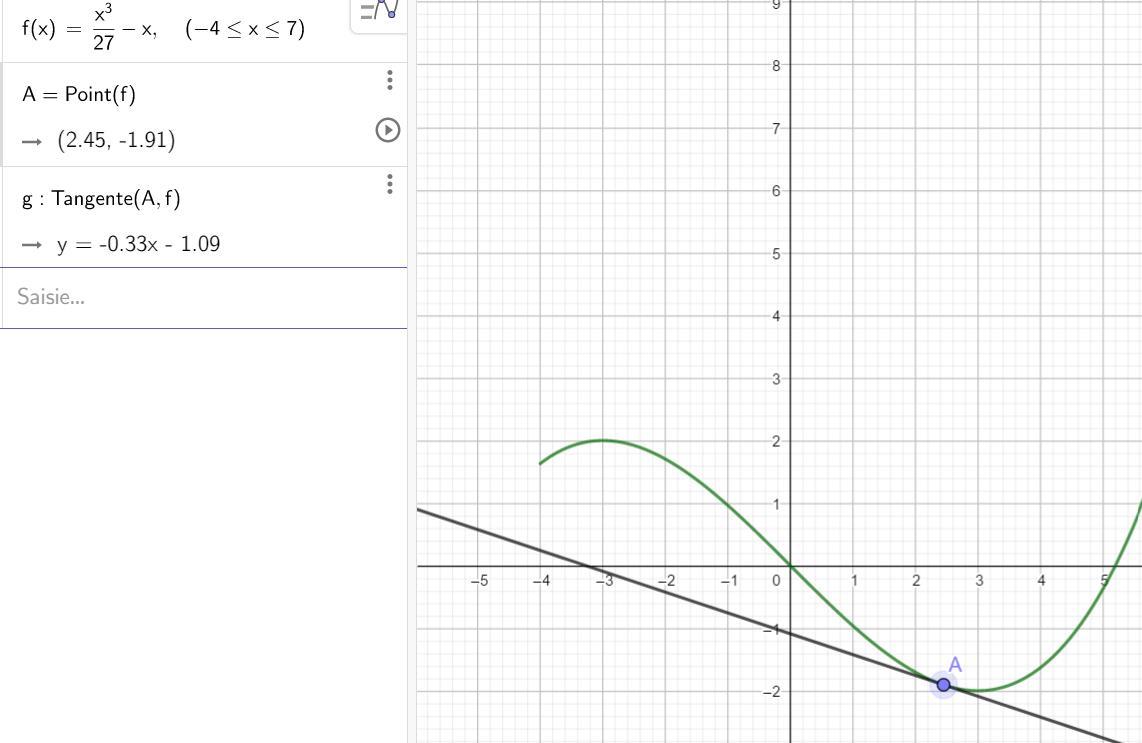
2. a. Quelle est la valeur du minimum sur l’intervalle ouvert ]2;4[ ?
b. Déterminer graphiquement la valeur de f'(3).
c. Quel est le signe de la dérivée pour les valeurs de x inférieures à 3 ? Quel est le signe de la dérivée pour les valeurs de x supérieures à 3?
Définition
On considère une fonction f définie sur un intervalle I .
On dit que la fonction f admet un extrémum local en \alpha s’il existe un intervalle ouvert J inclus dans I tel que f admette un extremum sur J en \alpha .
exemple : dans l’activité , 2 est un extremum local car c’est un maximum sur l’intervalle ouvert ]-3.5;-2.5[ et -2 est un extremum local car c’est un minimum sur l’intervalle ouvert ]2;4[
Théorème
On considère une fonction f dérivable sur un intervalle ouvert I et a un réel de I .
Si f’ s’annule en changeant de signe en a alors f admet un extremum local en a.
Exemple : Dans l’activité 2, f’ s’annule en -3 en changeant de signe donc f admet un extremum local en -3 , la valeur de cet extremum qui est un maximum est 2.
Dans l’activité 2, f’ s’annule en 3 en changeant de signe donc f admet un extremum local en 3 , la valeur de cet extremum qui est un minimum est -2.
Théorème
On considère une fonction f dérivable sur un intervalle ouvert I et un réel a de I.
Si f admet un extremum local en a alors f'(a)=0 et la tangente à la courbe au point d’abscisse a est parallèle à l’axe des abscisses.