Sommaire
Probabilités conditionnelles et indépendance
1. Probabilité de B sachant A
Activité d’approche
Dans une université, une enquête sur le tabagisme a donné les résultats suivants :
Il y a 700 hommes parmi les 1000 personnes qui ont été interrogées.
Parmi les 495 fumeurs, 420 sont des hommes.
On choisit au hasard l’une des 1000 personnes interrogées.
On note A l’évènement “la personne interrogée fume” et on note B l’évènement “la personne interrogée est une femme”.
- Recopier et compléter le tableau suivant
| A | \bar A | TOTAL |
B |
|
|
|
\bar B |
|
|
|
TOTAL |
|
|
|
2. a. Calculer la probabilité de l’évènement A que l’on note p(A) .
2. b. Décrire par une phrase l’évènement A\cap B puis calculer sa probabilité p(A\cap B) .
2. c. Calculer alors \frac{p(A\cap B)}{p(A)} .
2. d. Sachant que la personne choisie est une femme, quelle est la probabilité qu’elle fume ? Comparer le résultat obtenu au résultat de la question 2.c.
Définition
A et B sont deux évènements avec p(A)\ne 0.
La probabilité de l’évènement B sachant A est définie par p_A(B)=\frac{p(A\cap B)}{p(A)}.
Dans ce cas précis la condition est A, c’est cet évènement qui est écrit juste après sachant que.
Exercice n°1
En utilisant l’énoncé de l’activité précédente et la définition répondre aux questions suivantes :
- Sachant que la personne choisie fume, quelle est la probabilité qu’elle soit un homme ?
2. Sachant que la personne choisie est un homme, quelle est la probabilité qu’il fume ?
Exercice n°2
Dans un club de sport comportant 120 membres, 30% sont des femmes. Chaque membre ne pratique qu’un seul sport.
La moitié des membres fait du tennis, il y a autant de membres faisant de la natation que de membres faisant du golf.
Il y a deux fois plus de femmes pratiquant la natation que d’hommes pratiquant la natation.
15 % des membres pratiquant le tennis sont des femmes.
- Reproduire et compléter le tableau suivant
| tennis | natation | golf | total |
Femmes
|
|
|
|
|
Hommes
|
|
|
|
|
Total
|
|
|
|
|
2. On note T le membre choisi pratique le tennis.
On note F le membre choisi est une femme.
a. Calculer p(T).
b. Décrire en langue française l’évènement F\cap T puis calculer p(F\cap T).
c. Sachant qu’on a choisi une personne pratiquant le tennis, quelle est la probabilité que ce soit une femme ?
2. Probabilité de A\cap B
Propriété
A et B sont deux évènements avec p(A)\ne 0.
La probabilité de l’évènement A\cap B est p(A\cap B)={p(A)}\times{p_A(B)}.
Remarque : si p(B)\ne 0 on a de façon analogue p(A\cap B)={p(B)}\times{p_B(A)}.
3. Indépendance de deux évènements
définition
Dire que deux évènements A et B sont indépendants signifie que p(A\cap B)={p(A)}\times{p(B)}.
4. Tableau
| B | \bar B | TOTAL | |
| A | p(A\cap B) | p(A\cap {\bar B}) | p(A ) |
| \bar A | p(\bar{A}\cap B) | p(\bar A\cap {\bar B}) | p(\bar A ) |
| TOTAL | p(B ) | p(\bar B ) | 1 |
Exercice n°3
Dans une urne se trouvent 50 jetons.
30 sont noirs, les autres sont bleus.
25 sont carrés, les autres sont ronds.
Il y a 10 jetons noirs et carrés.
On choisit un jeton dans l’urne.
On note N : le jeton tiré est noir.
B: le jeton tiré est bleu.
C : le jeton tiré est carré .
R: le jeton tiré est rond.
- Reproduire et compléter le tableau suivant avec des probabilités.
| N | B | TOTAL | |
| C | |||
| R | |||
| TOTAL | 1 |
2. A l’aide du tableau précédent, préciser la probabilité des évènements suivants : N, B, C,N\cap C , R\cap B et R\cap N
3. Déduire de la question précédente p_N(R), p_B(R) et p_C(N).
Exercice n°4
Dans une classe de seconde il y a 32 élèves.
8 sont externes, les autres sont demi-pensionnaires.
18 font de l’allemand , les autres font de l’italien.
Il y a 5 externes qui font de l’italien.
On choisit un élève au hasard.
On note E : l’élève est externe.
D: l’élève est demi-pensionnaire.
A : l’élève fait de l’allemand .
I: l’élève fait de l’italien.
- Reproduire et compléter le tableau suivant avec des probabilités.
| E | D | TOTAL | |
| A | |||
| I | |||
| TOTAL | 1 |
2. A l’aide du tableau précédent, préciser la probabilité des évènements suivants : l’élève choisi est un externe, l’élève choisi fait de l’allemand, l’élève choisi fait de l’allemand et est demi-pensionnaire et l’élève choisi fait de l’italien et est externe.
3. a) Sachant que l’élève choisi est externe, quelle est la probabilité qu’il fasse de l’italien ?
3. b) Sachant que l’élève choisi fait de l’allemand, quelle est la probabilité qu’il soit demi-pensionnaire ?
Arbres pondérés
Activité d’approche
Dans une urne, se trouvent 4 boules rouges et 4 boules noires.
On tire une boule de l’urne, on note sa couleur. Sans remettre la boule dans l’urne on en tire une seconde et on note sa couleur.
On note R, l’évènement la boule tirée est rouge.
On note N, l’évènement la boule tirée est noire.
Partie 1 : On suppose que la première boule tirée est rouge.
- Calculer la probabilité que la première boule tirée est rouge.
2. Calculer la probabilité que la deuxième boule tirée est rouge sachant que la première boule tirée est rouge.
Partie 2 : On suppose que la première boule tirée est noire
- Calculer la probabilité que la première boule tirée est noire.
2. Calculer la probabilité que la deuxième boule tirée est rouge sachant que la première boule tirée est noire.
Partie 3 :
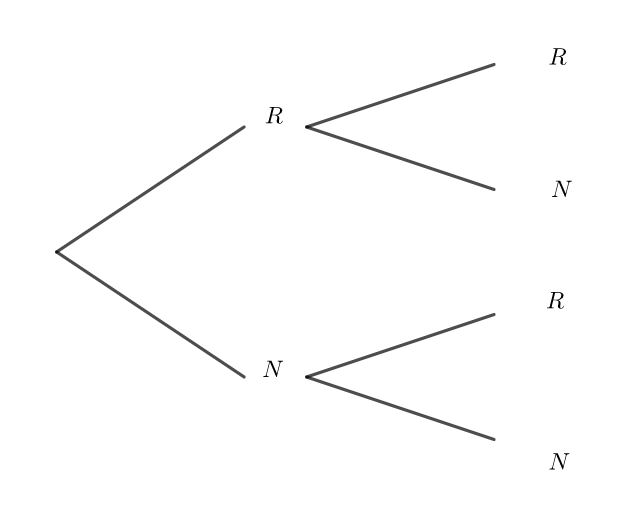
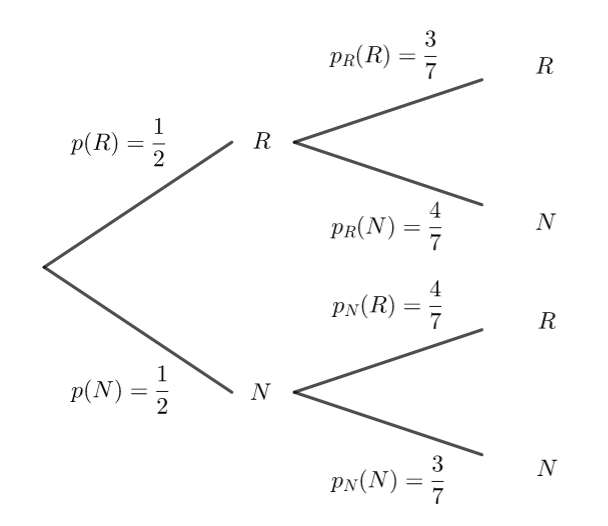
En utilisant les résultats des parties 1 et 2, compléter l’arbre suivant qui représente l’expérience.
Exercice n°5:
Dans un pays, il y a 2 % de la population contaminée par un virus.
On dispose d’un test de dépistage d’un virus qui a les propriétés suivantes :
– La probabilité qu’une personne contaminée ait un test positif est de 0,99 (sensibilité du test).
– La probabilité qu’une personne non contaminée ait un test négatif est de 0,97 (spécificité du
test).
On fait passer un test à une personne choisie au hasard dans cette population.
On note V l’évènement « la personne est contaminée par le virus » et T l’évènement « le test est positif ».
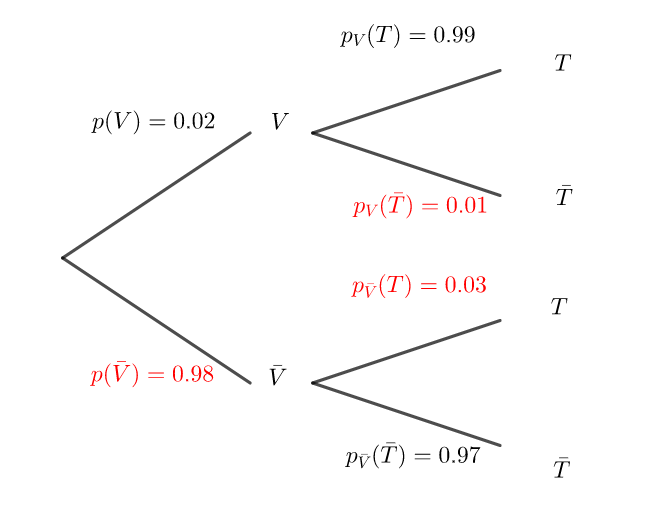
\bar{V}et \bar{T} désignent respectivement les évènements contraires de V et T .
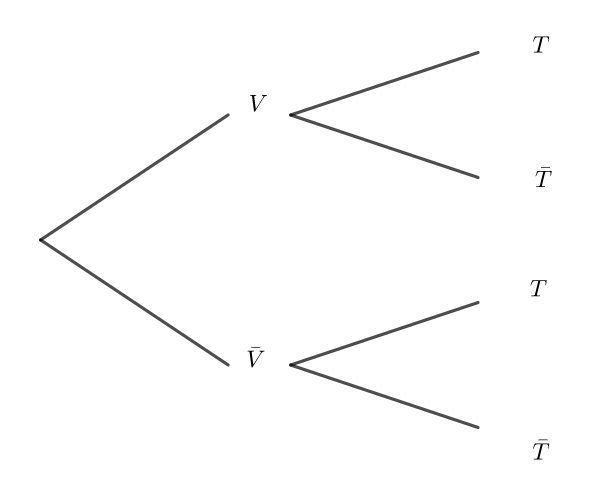
Préciser les valeurs des probabilités p(V), p_V(T) et p_{\bar{V}}(\bar{T}) puis compléter l’arbre ci-dessous.
Probabilités totales
Activité d’approche
Dans un parc, se trouvent deux bassins contenant des poissons. On les nommera respectivement A et B.
Dans le bassin A, il y a 4 carpes et 8 perches.
Dans le bassin B, il y a 8 carpes et 2 perches.
- Un pêcheur s’installe au bord du bassin A.
Quelle est la probabilité qu’il pêche une carpe ? Une perche ?
2. Le pêcheur s’installe ensuite au bord du bassin B.
Quelle est la probabilité qu’il pêche une carpe ? Une perche ?
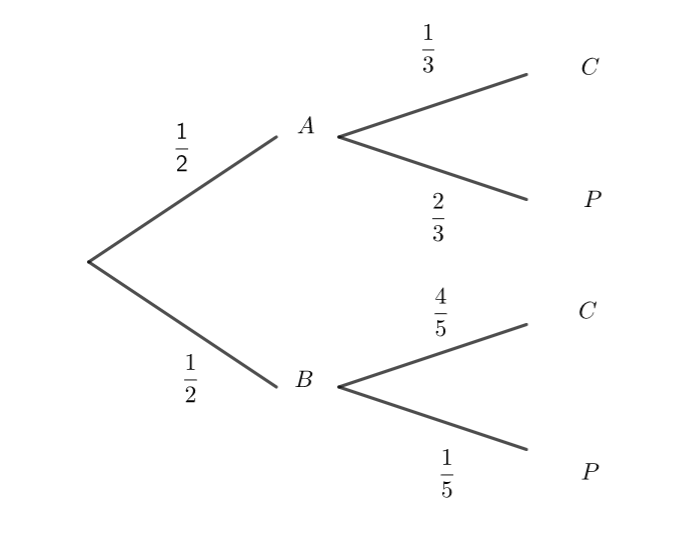
3. On propose ensuite l’expérience suivante : le pêcheur choisit au hasard l’un des deux bassins ( chaque bassin a la même probabilité d’être choisi ).
On note A l’évènement : le pêcheur a choisi le bassin A.
On note B l’évènement : le pêcheur a choisi le bassin B.
On note C l’évènement : le pêcheur a pêché une carpe .
On note P l’évènement : le pêcheur a pêché une perche.
a. Recopier l’arbre suivant et compléter les pointillés par les nombres trouvés dans les questions 1 et 2.
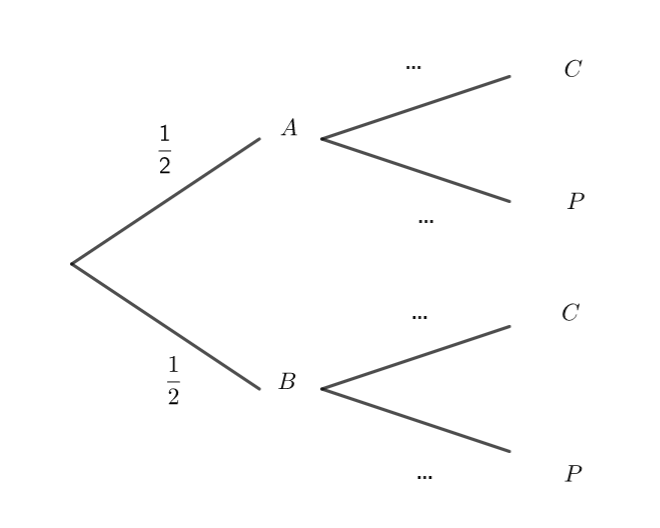
b. Calculer p(A\cap C), puis p(B\cap C).
c. Peut-on en déduire p( C)?
Propriété
Sur un arbre pondéré, la probabilité d’un évènement E est la somme des probabilités de tous les chemins qui mènent à E.
Remarque : pour l’activité précédente p(C)=p(A\cap C)+p(B\cap C)
Exercice n°6
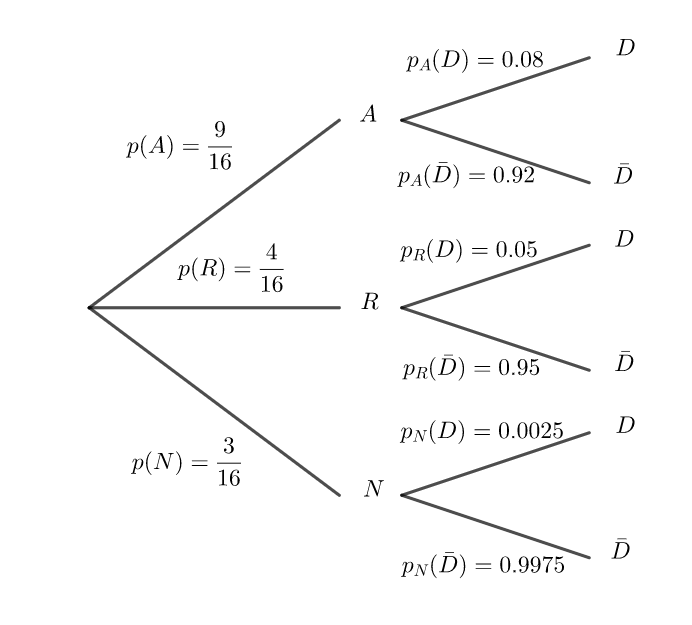
Une entreprise de transports routiers dispose de 16 camions dont :
• 9 sont considérés comme « anciens »
• 4 sont considérés comme « récents »
• 3 sont considérés comme « neufs ».
L’entreprise décide d’observer l’état des 16 camions pendant une période donnée. On sait de plus
que, pendant cette période, la probabilité que :
• un camion « ancien » ait une panne, est égale à 0,08
• un camion « récent » ait une panne, est égale à 0,05
• un camion « neuf » ait une panne, est égale à 0,002 5.
On choisit au hasard un camion parmi les 16. On note les évènements suivants :
A : « le camion est ancien »
R : « le camion est récent »
N : « le camion est neuf »
D : « le camion a une panne ».
1. Reproduire et compléter l’arbre pondéré ci-dessous.
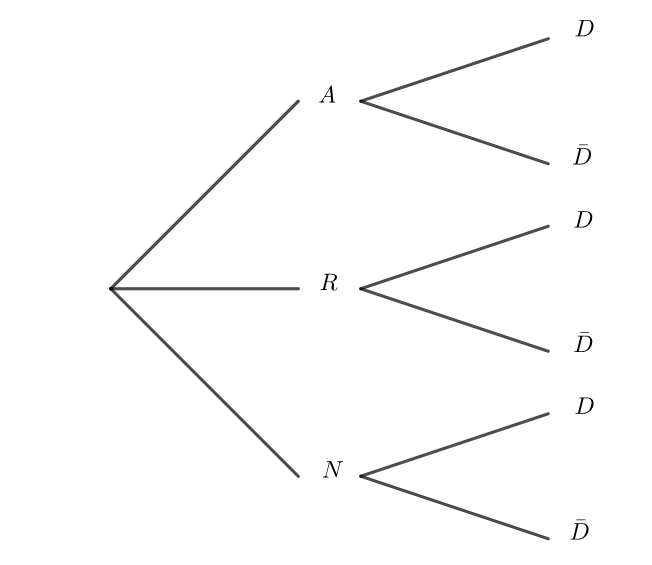
2. Calculer p(R\cap D).
3. Calculer p(D)
4. Calculer la probabilité que le camion soit récent sachant qu’il a une panne.
Exercice n°7 :
Dans un aéroport, les portiques de sécurité servent à détecter les objets métalliques que peuvent
emporter les voyageurs.
On choisit au hasard un voyageur franchissant un portique.
On note :
S l’évènement « le voyageur fait sonner le portique »;
M l’évènement « le voyageur porte un objet métallique ».
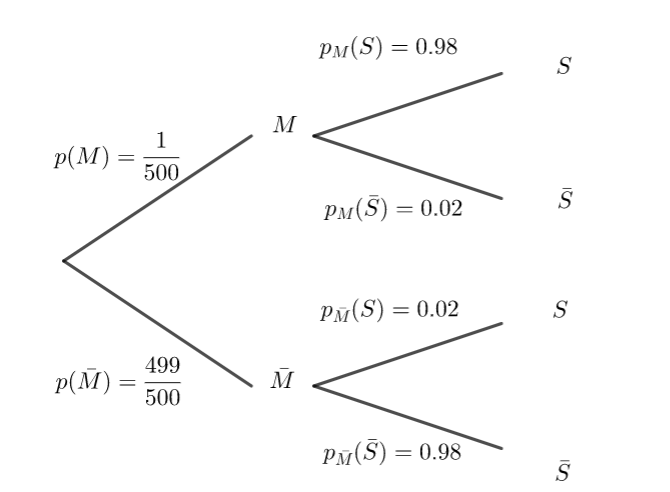
On considère qu’un voyageur sur 500 porte sur lui un objet métallique.
1. On admet que :
Lorsqu’un voyageur franchit le portique avec un objet métallique, la probabilité que le
portique sonne est égale à 0,98;
Lorsqu’un voyageur franchit le portique sans objet métallique, la probabilité que le portique ne sonne pas est aussi égale à 0,98.
À l’aide des données de l’énoncé, préciser les valeurs de p(M), p_M(S)et p_{\bar{M}}(\bar{S})
2. Recopier et indiquer les probabilités sur les branches de l’arbre pondéré ci-dessous illustrant la situation.
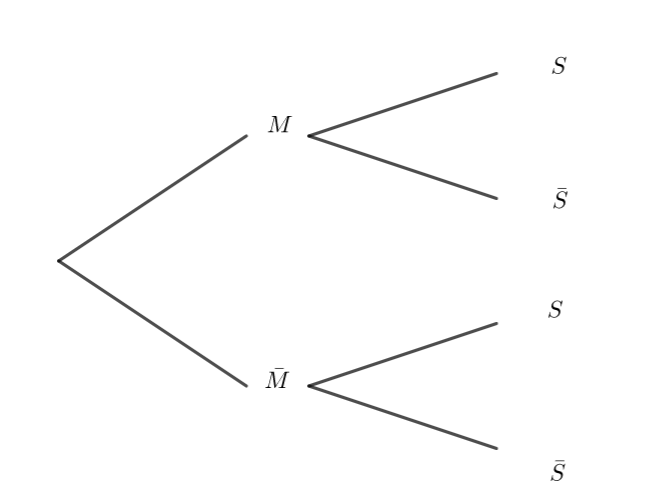
3. Montrer que : p(S)=0.02192.
4. En déduire la probabilité qu’un voyageur porte un objet métallique sachant qu’il a fait
sonner le portique.