Sommaire
Vocabulaire
Dans une succession de deux épreuves lorsque l’issue de la première n’influe pas sur le résultat de la seconde , on dit que ces épreuves sont indépendantes.
Exemple n°1
On jette une pièce de monnaie deux fois de suite et on note les résultats obtenus.
Ces deux épreuves sont bien indépendantes.
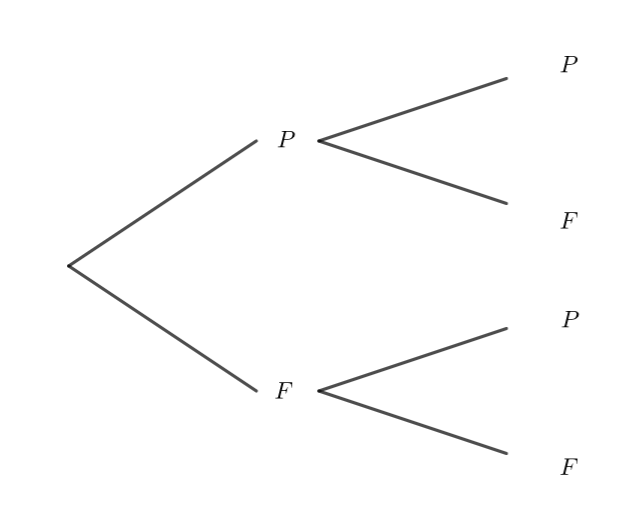
- Représenter la situation à l’aide d’un arbre ( on notera F le résultat est face et P le résultat est pile )
2. Calculer p(PP).
Exemple n°2
On jette un dé équilibré deux fois de suite.
Ces deux épreuves sont bien indépendantes.
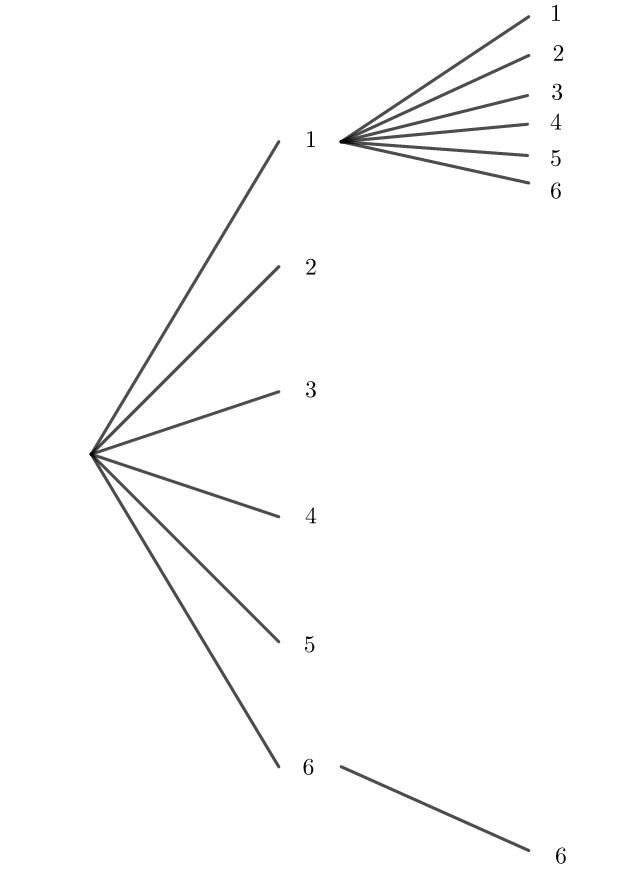
- Représenter la situation à l’aide d’un arbre incomplet ( utiliser les chiffres de 1 à 6 et des pointillés)
2. Calculer p(66).
Propriété admise
Dans une répétition d’épreuves indépendantes, la probabilité d’une issue est le produit des probabilités des branches qui constituent le chemin qui mène à cette issue.
Exemple n°1 (suite)
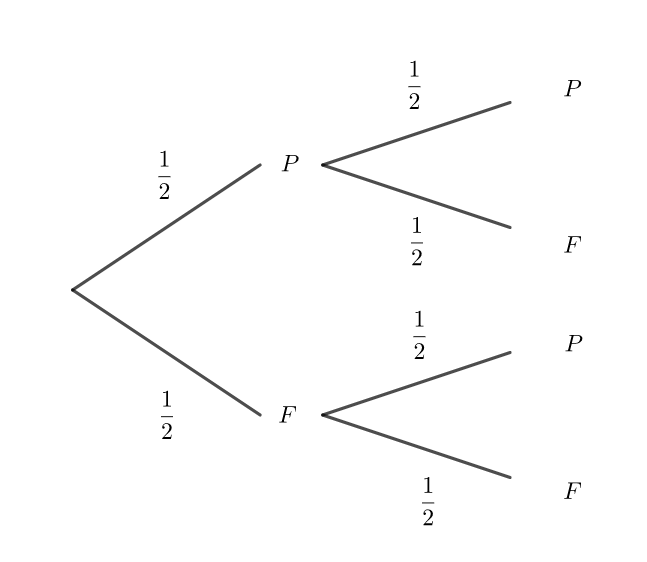
On jette une pièce de monnaie deux fois de suite et on note les résultats obtenus.
Calculer p(PP) en utilisant la propriété ci-dessus.
Exemple n°2 (suite)
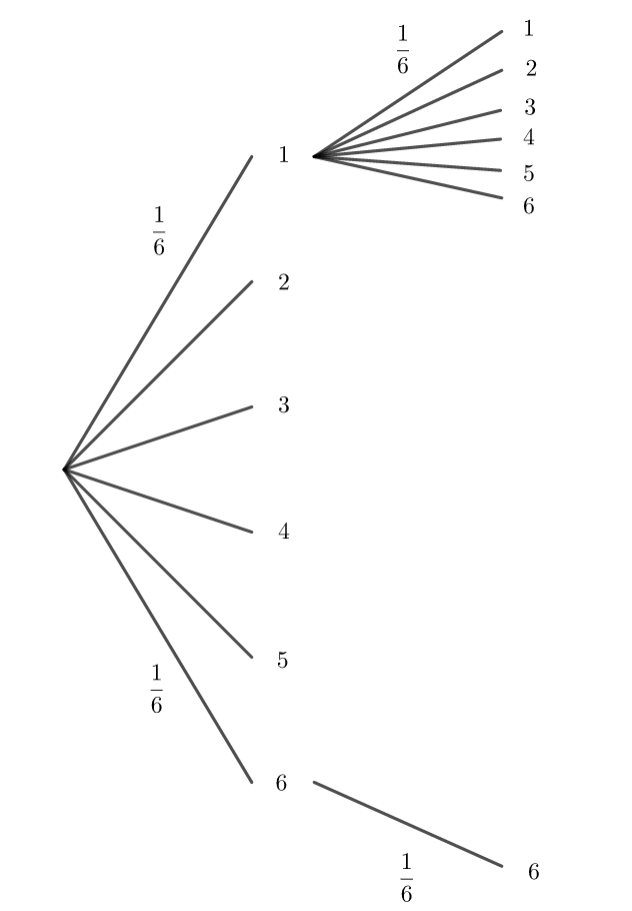
On jette un dé équilibré deux fois de suite et on note les résultats obtenus.
Calculer p(66) en utilisant la propriété ci-dessus.
Exemple n°3
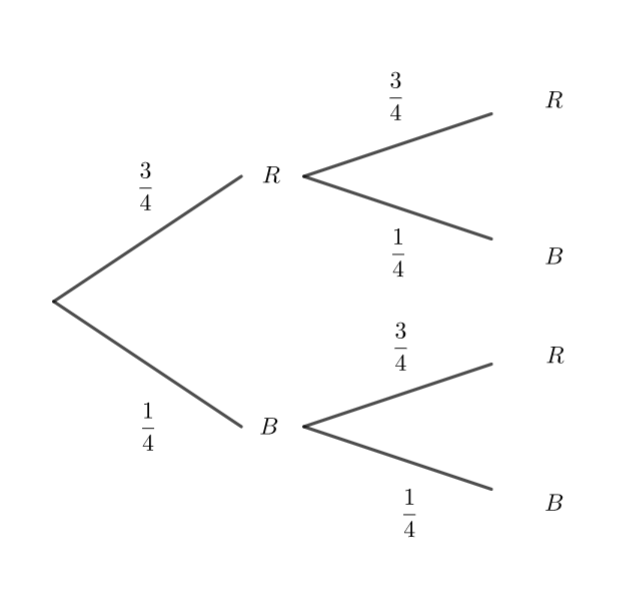
On tire une boule dans une urne qui en contient 3 rouges et une bleue, on note sa couleur , on la remet dans l’urne et on en tite une seconde.
Ces deux épreuves sont bien indépendantes.
- Représenter la situation à l’aide d’un arbre ( utiliser les lettres R et B)
2. Calculer p(RB) .
Pour aller plus loin avec les exercices vus dans le cours Probabilités conditionnelles.
Exercice n°7
En voici un exemple, reprenons l’exercice n°7 et rajoutons la question n°5.
Dans un aéroport, les portiques de sécurité servent à détecter les objets métalliques que peuvent
emporter les voyageurs.
On choisit au hasard un voyageur franchissant un portique.
On note :
S l’évènement « le voyageur fait sonner le portique »;
M l’évènement « le voyageur porte un objet métallique ».
On considère qu’un voyageur sur 500 porte sur lui un objet métallique.
1. On admet que :
Lorsqu’un voyageur franchit le portique avec un objet métallique, la probabilité que le
portique sonne est égale à 0,98;
Lorsqu’un voyageur franchit le portique sans objet métallique, la probabilité que le portique ne sonne pas est aussi égale à 0,98.
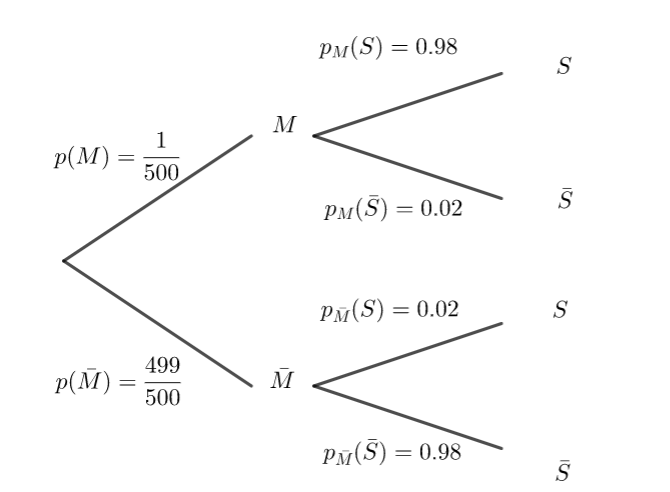
À l’aide des données de l’énoncé, préciser les valeurs de p(M), p_M(S)et p_{\bar{M}}(\bar{S})
2. Recopier et indiquer les probabilités sur les branches de l’arbre pondéré ci-dessous illustrant la situation.
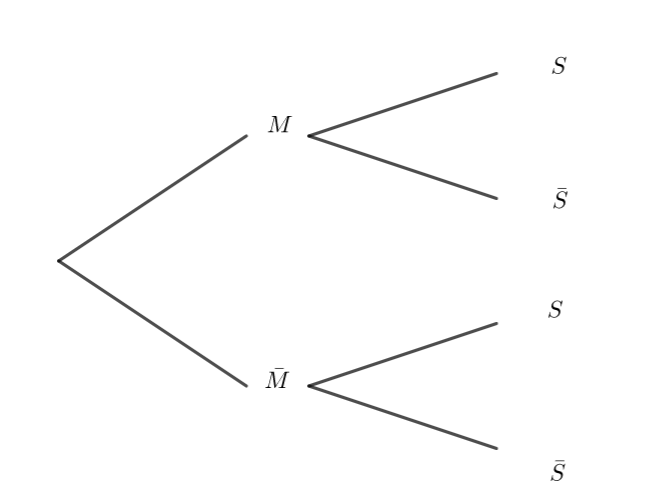
3. Montrer que : p(S)=0.02192.
4. En déduire la probabilité qu’un voyageur porte un objet métallique sachant qu’il a fait
sonner le portique.
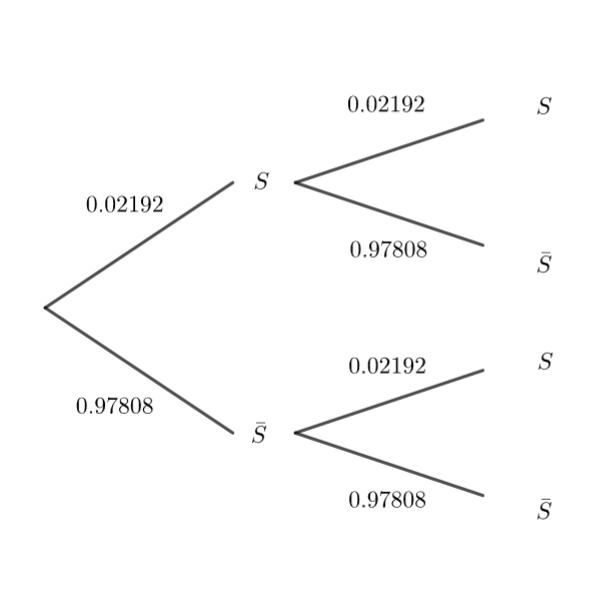
5. On décide que la personne passe deux fois sous le portique et on admet que ces deux passages sont indépendants. Quelle est la probabilité que le portique sonne lors des deux passages ?
Exercice n°8
En voici un exemple, reprenons l’exercice n°8 et rajoutons la question n°3.
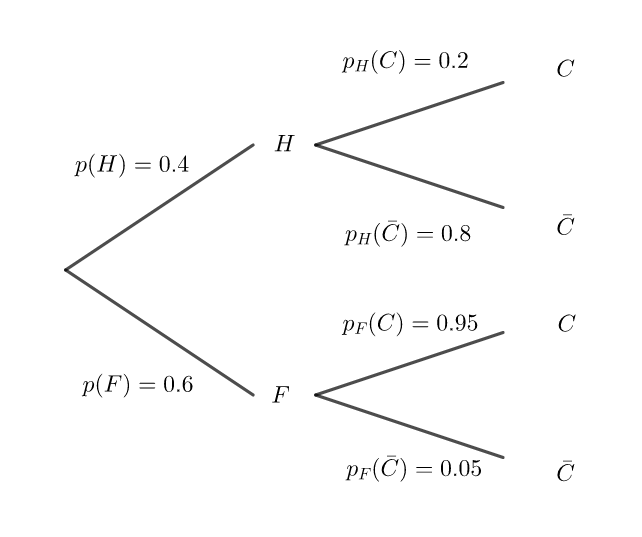
Un club de remise en forme propose, outre l’accès aux salles de musculation, des cours collectifs pour lesquels un supplément est demandé lors de l’inscription. Une fiche identifie chaque membre et son type d’abonnement : avec ou sans cours collectif.
Une étude sur les profils des membres de ce club a montré que :
40 % des membres sont des hommes.
65 % des membres sont inscrits aux cours collectifs.
Parmi les femmes, membres de ce club, seulement 5 % ne sont pas inscrites aux cours collectifs.
On choisit une fiche au hasard et on considère les évènements suivants :
— H : « la fiche est celle d’un homme »,
— F : « la fiche est celle d’une femme »,
— C : « la fiche est celle d’un membre inscrit à des cours collectifs ».
Rappel de notation : Si A et B sont deux évènements donnés, p(A) désigne la probabilité de A et
p_B(A) désigne la probabilité conditionnelle de A sachant B.
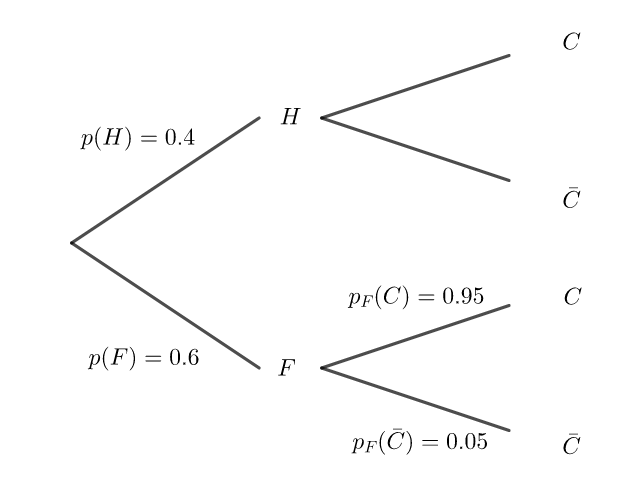
1. Préciser les probabilités suivantes : p(H) , p_F(\bar{C}) et p_F(C) puis les reporter sur l’arbre pondéré ci-dessous qu’on complètera au fur et à mesure.
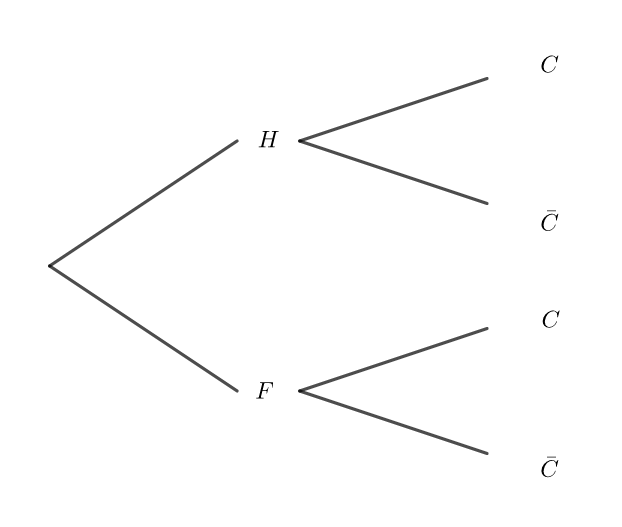
2. a. Déterminer p(F ∩C).
b. Montrer que p(H ∩C) = 0,08.
c. On tire la fiche d’un homme, quelle est la probabilité que celui-ci soit inscrit aux cours
collectifs ?
d. Compléter l’arbre pondéré de la question 1.
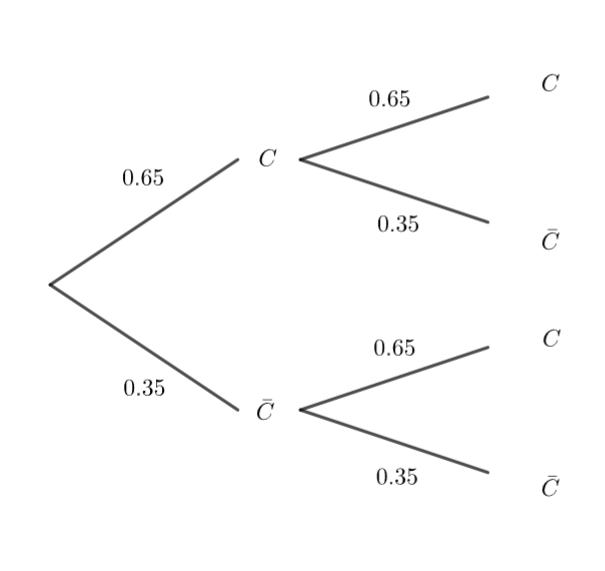
3. On tire au hasard une fiche d’un membre du club puis on la remet dans la boîte; on tire ensuite une seconde fiche d’un membre du club et on admet que ces deux tirages sont indépendants. Quelle est la probabilité que les deux fiches tirées soient des fiches de membres inscrits aux cours collectifs ?