Sommaire
Exercice n°1
Une agence propose deux formules pour se rendre en Grèce : train ou avion.
De plus, s’ils le souhaitent, ils peuvent compléter leur formule par l’option « location de voiture sur place».
75 % des clients optent pour l’avion ;
parmi les clients ayant choisi le train, 50 % choisissent aussi l’option « location de voiture sur place » ;
12 % des clients ont choisi à la fois l’avion et l’option « location de voiture sur place ».
On interroge au hasard un client de l’agence .
On considère les évènements suivants :
A : « le client a choisi l’avion » ;
V : « le client a choisi l’option location de voiture sur place ».
1) Déterminer p_A(V) .
2) Démontrer que la probabilité pour que le client interrogé ait choisi l’option
« location de voiture sur place » est égale à 0.245
3) Calculer la probabilité pour que le client interrogé ait pris l’avion sachant qu’il
n’a pas choisi l’option « location de voiture sur place ». Arrondir le résultat au centième.
4) On interroge au hasard deux clients de manière aléatoire et indépendante.
Quelle est la probabilité qu’aucun des deux ne prennent l’option « location de voiture sur place » ?
Exercice n°2
Dans tout l’exercice, les résultats seront arrondis, si nécessaire, au dix millième.
On étudie un test antigénique pour dépister la COVID 19.
On sait que 6% de la population est atteint de la maladie. Des études ont montré que si une
personne est malade, alors le test se révèle positif dans 60% des cas et si une personne n’est
pas malade, le test est négatif dans 93% des cas.
Pour une personne à qui on fait passer le test de dépistage on associe les événements :
V : la personne a contracté le virus,
T : le test est positif.
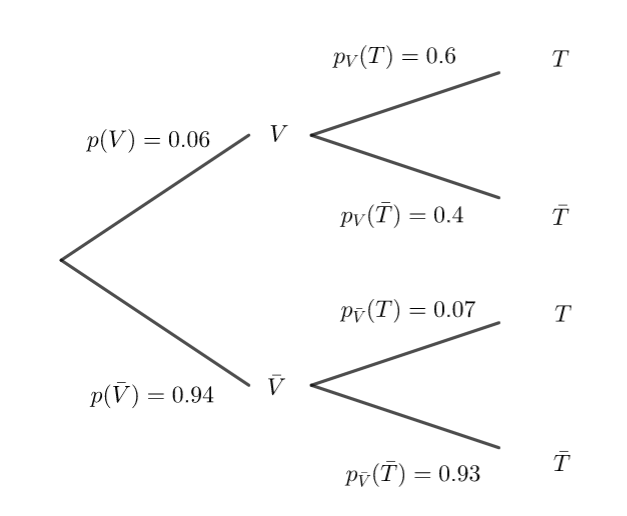
1. Recopier et compléter sur la copie l’arbre de probabilité suivant en utilisant les données de
l’exercice.
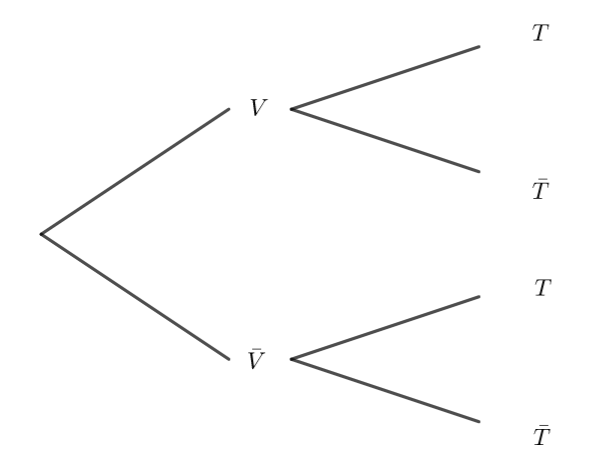
2. Justifier que p(V ∩ 𝑇) =0.036 .
3. Montrer que p( 𝑇) =0.1018
4. Calculer p_T(V) .
5. Une personne dont le test se révèle positif est-elle nécessairement atteinte par cette maladie ?
Exercice n°3
Un modèle de puce informatique nécessaire à la fabrication d’un smarphone d’une grande entreprise est produit par deux fabriquants A et B.
Chez le sous-traitant A, qui assure 25% de la production totale, 8 % des téléphones sont défectueux.
Le sous-traitant B assure le reste de la production.
On constate que la probabilité qu’un téléphone pris au hasard dans les stocks de l’entreprise soit défectueux est de 0.05 .
1) Quel pourcentage de la production totale le sous-traitant B assure-t-il ?
2) Quelle est la probabilité qu’un téléphone proviennent du sous-traitant B sachant
qu’il est défectueux ?
Exercice n°4
Une étude statistique menée lors des entraînements de tir à l’arc montre que Michel
plante la flèche dans la cible avec une probabilité de 0,8.
Michel effectue une série de 3 tirs . Les deux issues possibles après chaque tir sont les
événements :
T : « Michel touche la cible » ;
M : « Michel manque la cible ».
On admet que les tirs de Michel sont indépendants.
1. On note 𝑋 la variable aléatoire qui prend pour valeur le nombre total de fois que Michel touche la cible.
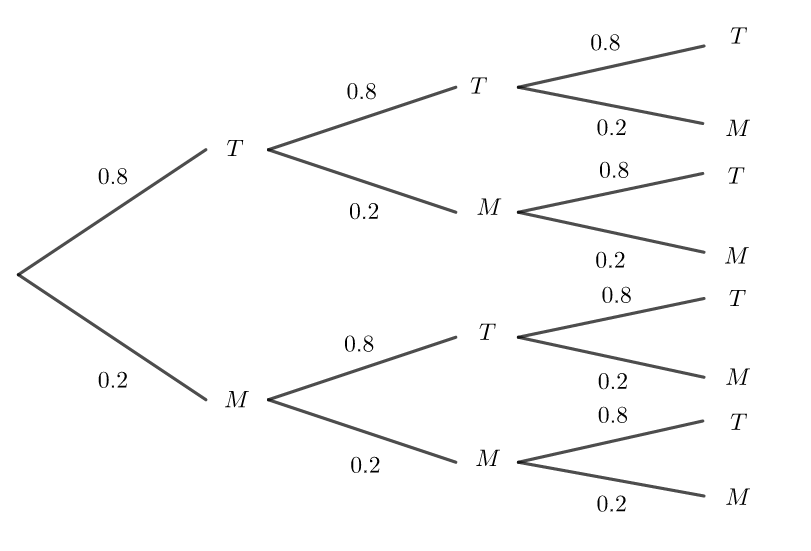
a. Réaliser un arbre pondéré permettant de décrire toutes les issues possibles.
b. Déterminer la loi de probabilité de 𝑋.
c. Calculer l’espérance 𝐸(𝑋) de la variable aléatoire 𝑋.
2. On imagine le jeu suivant : on mise 10 € avant la série de tirs de Michel .
Chaque fois qu’il touche la cible Michel reçoit 5 euros, et chaque fois que Michel ne touche pas la cible, il ne reçoit rien.
On note 𝑌 la variable aléatoire qui prend pour valeur le gain algébrique du spectateur, c’està-dire la différence entre le gain total obtenu et la mise engagée.
a. Exprimer 𝑌 en fonction de 𝑋.
b. En déduire l’espérance 𝐸(𝑌) de la variable aléatoire 𝑌. Interpréter ce résultat dans le contexte de l’énoncé.
Exercice n°5
Un restaurant propose à sa carte deux desserts différents :
-le premier dessert est un fondant au chocolat, et est choisi par 50 % des
clients,
-le second dessert est une île flottante, et est choisie par 25 % des clients.
Les autres clients ne prennent pas de dessert. Aucun client ne prend plusieurs desserts.
Le restaurateur a remarqué que parmi les clients ayant pris comme dessert le fondant au chocolat, 75 % prennent un café, que parmi les clients ayant pris comme dessert une
île flottante, 25 % prennent un café et que parmi les clients n’ayant pas pris de dessert,
80 % prennent un café. On interroge au hasard un client.
On note :
F l’évènement : « Le client prend fondant au chocolat. »
I l’évènement : « Le client prend une île flottante. »
R l’évènement : « Le client ne prend pas de dessert. »
C l’évènement : « Le client prend un café. »
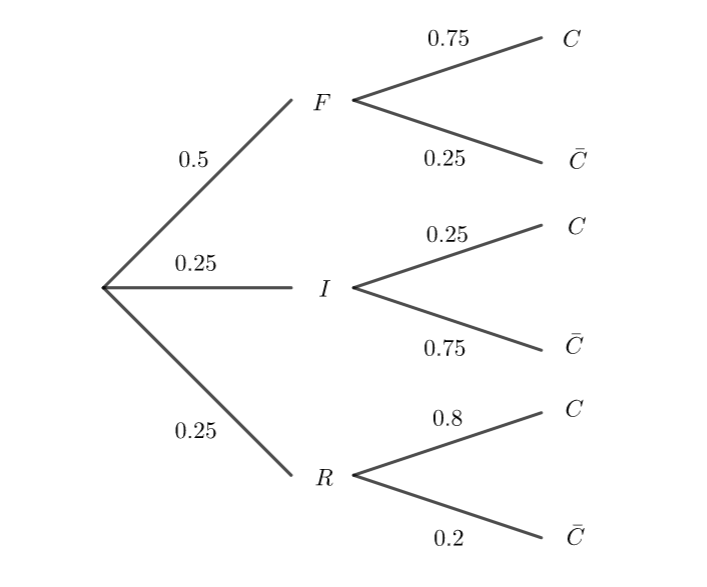
1. Construire un arbre de probabilités décrivant la situation.
2. Définir par une phrase les probabilités p(I\cap C) et p_C( F)(on ne demande pas de les calculer).
3. Calculer p(I\cap C) puis p( C).
4. On rencontre un client ayant pris un café. Quelle est la probabilité qu’il ait pris une île flottante ?
Exercice n°6
Alain participe à un jeu télévisé.
Les questions portent sur la musique et se répartissent en trois catégories : Rock, Variérés et Classique.
Alain sait qu’il a
3 chances sur 4 de donner la bonne réponse sachant qu’il est interrogé sur le Rock ;
4 chances sur 5 de donner la bonne réponse sachant qu’il est interrogé sur les
Variétés ;
1 chance sur 8 de donner la bonne réponse sachant qu’il est interrogé sur la musique
classique.
On note :
R l’événement : « Alain est interrogé sur le Rock » ;
V l’événement : « Alain est interrogé sur les Variétés »
C l’événement : « Alain est interrogé sur la musique classique »
B l’événement : « Alain donne la bonne réponse »
Dans chaque catégorie, il y a le même nombre de questions. On admet donc que
p(R)=p(V)=p(C)=\frac{1}{3}
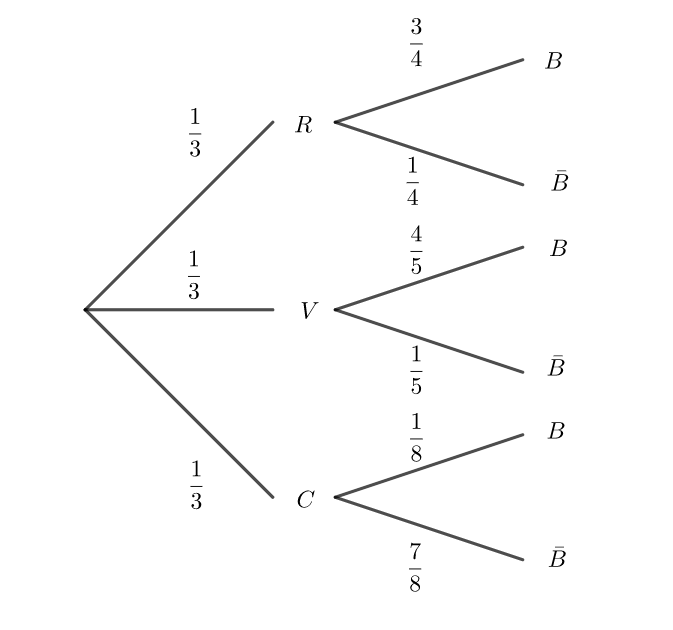
1. Construire un arbre pondéré décrivant la situation.
2. Alain tire au hasard une question. Montrer que p(B)=\frac{67}{120} .
3. Pour participer à ce jeu, Alain doit payer 10 € de droit d’inscription. Il recevra :
12 € s’il est interrogé en Rock et que sa réponse est bonne ;
10 € s’il est interrogé en Variétés et que sa réponse est bonne ;
50 € s’il est interrogé en Classique et que sa réponse est bonne ;
rien si la réponse qu’il donne est fausse.
On note 𝑋 la variable aléatoire qui, à chaque partie jouée par Alain associe son gain
algébrique, c’est-à-dire la différence en euros entre ce qu’il reçoit et les 10 € de
droit d’inscription.
a. Montrer que p(X=40)=\frac{1}{24}
b. Déterminer la loi de probabilité de 𝑋.
c. Calculer l’espérance mathématique de 𝑋. Alain a-t-il intérêt à jouer ?
Exercice n°7
Un commerçant dispose dans sa boutique d’un terminal qui permet à ses clients, s’ils souhaitent
régler leurs achats par carte bancaire, d’utiliser celle-ci en mode sans contact (quand le montant de
la transaction est inférieur ou égal à 50 euros ou bien en mode code secret (quel que soit le montant de la transaction).
Il remarque que :
• 80 % de ses clients règlent des sommes inférieures ou égales à 50 euros. Parmi eux :
— 40 % paient en espèces;
— 40 % paient avec une carte bancaire en mode sans contact;
— les autres paient avec une carte bancaire en mode code secret.
• 20 % de ses clients règlent des sommes strictement supérieures à 50 euros. Parmi eux :
— 70 % paient avec une carte bancaire en mode code secret
— les autres paient en espèces.
On interroge au hasard un client qui vient de régler un achat dans la boutique.
On considère les évènements suivants :
V: « pour son achat, le client a réglé un montant inférieur ou égal à 50 euros »
E : « pour son achat, le client a réglé en espèces »
S: « pour son achat, le client a réglé avec sa carte bancaire en mode sans contact »
C: « pour son achat, le client a réglé avec sa carte bancaire en mode code secret »;
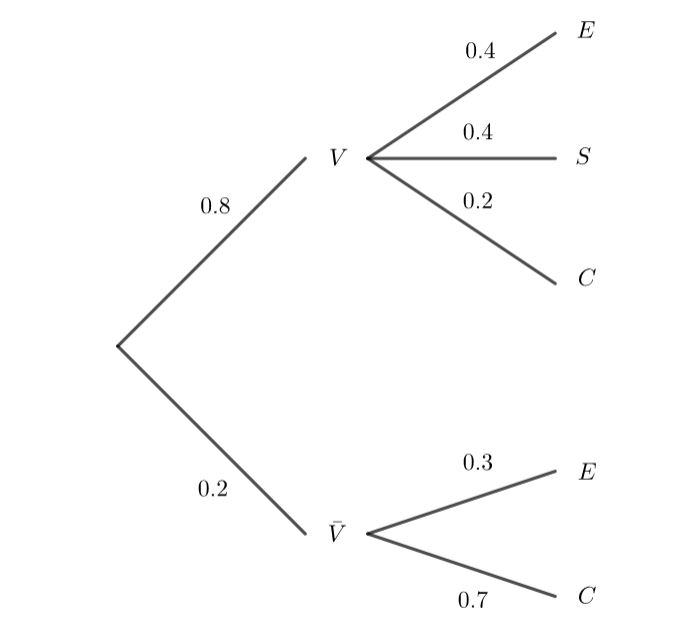
1. a. Donner la probabilité de l’évènement V , notée p(V) , ainsi que la probabilité de S sachant V notée p_V(S) .
b. Traduire la situation de l’énoncé à l’aide d’un arbre pondéré.
2. a. Calculer la probabilité que pour son achat, le client ait réglé un montant inférieur ou égal
à 50 euros et qu’il ait utilisé sa carte bancaire en mode sans contact.
b. Montrer que la probabilité de l’évènement : « pour son achat, le client a réglé avec sa carte
bancaire en utilisant l’un des deux modes » est égale à 0,62.
3. Sachant que le client a payé par carte bancaire en mode secret, montrer que la probabilité de l’évènement : le montant est inférieur ou égal à 50 euros est égale à 0.53
Exercice n°8
Un restaurant propose deux types de plats à emporter : le plat du jour et des pizzas.
Le restaurant propose également plusieurs desserts.
Le propriétaire constate que 60% des clients choisissent le plat du jour et que parmi ceux-ci 80% prennent également un dessert.
Elle constate aussi que 75 % des clients qui ont choisi une pizza ne prennent pas de dessert.
On choisit au hasard un client .
On considère les évènements suivants :
J : « Le client interrogé a choisi le plat du jour ».
D : « Le client interrogé a choisi un dessert ».
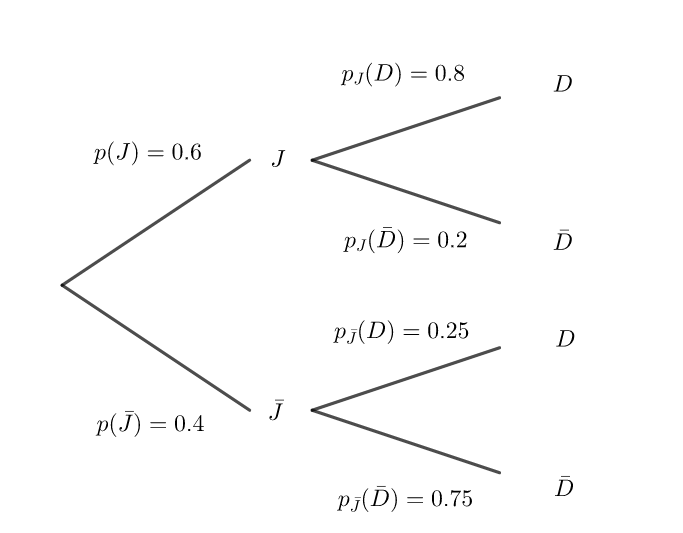
1. Recopier puis compléter l’arbre pondéré suivant :
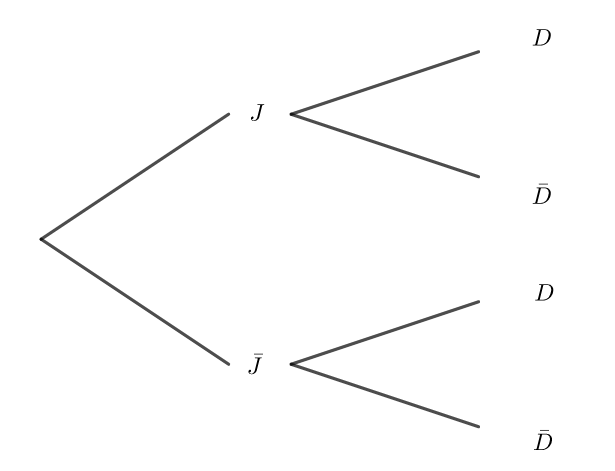
2. Calculer la probabilité que le client ait choisi un plat du jour et un dessert.
3. Démontrer que p(D)=0.58 .
4. Sachant que le client a acheté un dessert, quelle est la probabilité, arrondie à 0, 01 près, qu’il
ait acheté une pizza ?
5. Les événements J et D sont-ils indépendants ?
Exercice n°9
Pendant la semaine du blanc, une grande surface a mis en vente un lit à 499 euros et une parure de draps à 49 euros.
On a constaté que
40% des clients du magasin ont acheté un lit .
Parmi les clients ayant acheté un lit, 70 % ont acheté une parure de draps
Parmi les clients du magasin n’ayant pas acheté de lit, 25 % ont tout de même acheté une parure de draps.
On choisit au hasard un client. On admet qu’un client achète au plus un lit et au plus une parure de draps.
On note les événements suivants :
L « le client achète un lit »
D « le client achète une parure de draps ».
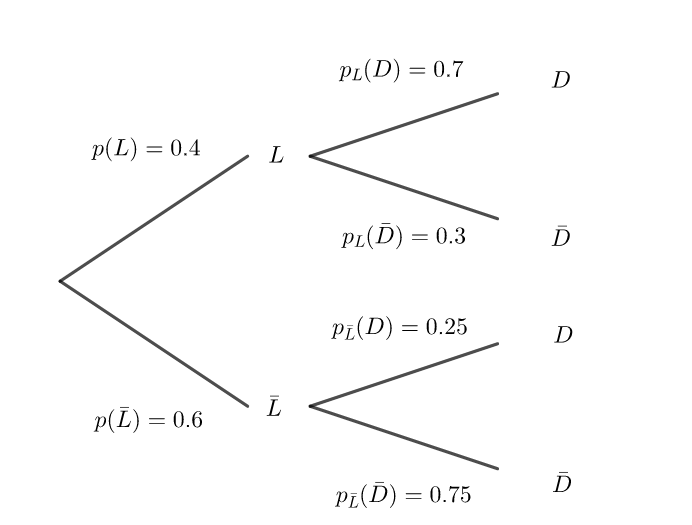
1. Reproduire sur la copie et compléter l’arbre pondéré ci-dessous décrivant la situation.
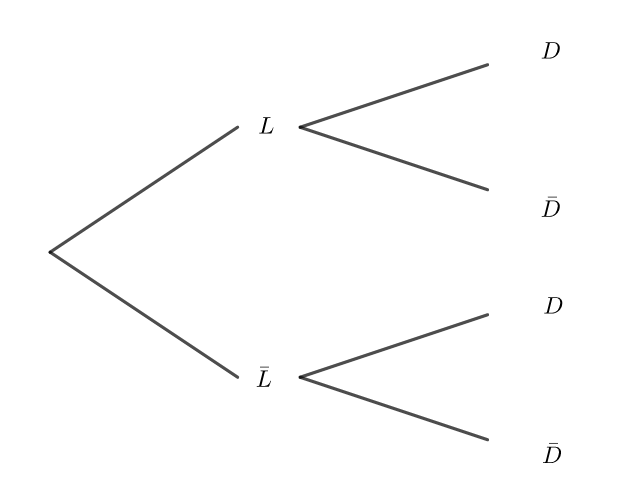
2. Calculer la probabilité que le client achète un lit et une parure de draps.
3. Montrer que la probabilité de l’événement D est égale à 0.43
.
4. Calculer la probabilité que le client achète un lit sachant qu’il a acheté une parure de draps.
5. On appelle S la variable aléatoire donnant la somme dépensée par un client au rayon literie.
Calculer l’espérance mathématique de 𝐷 et donner une interprétation de ce nombre dans le contexte de l’exercice.