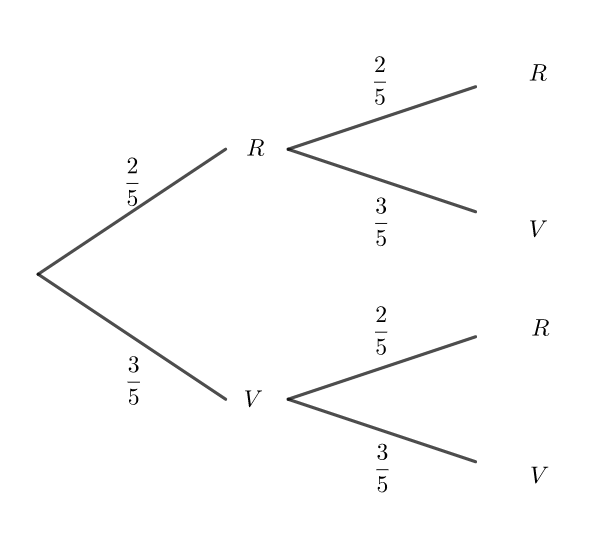
Variable aléatoire et loi de probabilité
Variable aléatoire
Définition
\Omega est l’univers d’une expérience aléatoire.
Définir une variable aléatoire, c’est associer à chaque issue de l’expérience un nombre réel.
Exemple n°1 :
On lance un dé équilibré.
- si le numéro sorti est 2 ou 4, on gagne 2 euros,
- si le numéro sorti est impair on gagne 1 euro
- si le 6 sort, on perd 6 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Par exemple à l’issue « le numéro sorti est le 5 », on associe la valeur +1 et à l’issue « le numéro sorti est le 6 », on associe la valeur -6 .
Exemple n°2 :
On lance deux fois de suite une pièce de monnaie.
- si on obtient deux fois pile, on gagne 2 euros
- si on obtient une seule fois pile , on gagne 1 euros
- sinon on perd 3 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Par exemple à l’issue PP, on associe la valeur +2 et à l’issue FF, on associe la valeur -3 .
Exemple n°3 :
On mise 3 euros.
Ensuite on tire une première boule dans une urne qui contient deux rouges et trois vertes, on la remet dans l’urne et on en tire une deuxième.
- si on obtient deux rouges, on gagne 6 euros
- si on obtient deux vertes , on gagne 3 euro
- sinon on on perd 1 euro.
On appelle X la variable aléatoire qui à une issue associe le gain algébrique en euros ( ne pas oublier la mise).
Par exemple à l’issue « les deux boules sont rouges », on associe la valeur 6-3=3 et à l’issue « les deux boules sont de couleur différente », on associe la valeur 3-3=0
Loi de probabilité
Définition
\Omega est l’univers d’une expérience aléatoire.
X est une variable aléatoire réelle définie sur \Omega qui prend les valeurs a_1, a_2, a_3 , …a_n
Définir la loi de probabilité de X, c’est associer à chaque valeur a_i , la probabilité p(X=a_i).
En général, on la présente sous forme de tableau
Valeur de X | a_1 | a_2 | … | a_n |
| P(X=a_i) | p_1 | p_2 | … | p_n |
Exemple n°1 (suite):
On lance un dé équilibré.
- si le numéro sorti est 2 ou 4, on gagne 2 euros,
- si le numéro sorti est impair on gagne 1 euro
- si le 6 sort, on perd 6 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Déterminer la loi de probabilité de la variable aléatoire X.
Exemple n°2 :
On lance deux fois de suite une pièce de monnaie.
- si on obtient deux fois pile, on gagne 2 euros
- si on obtient une seule fois pile , on gagne 1 euros
- sinon on perd 3 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Déterminer la loi de probabilité de la variable aléatoire X.
Exemple n°3 :
On mise 3 euros.
Ensuite on tire une première boule dans une urne qui contient deux rouges et trois vertes, on la remet dans l’urne et on en tire une deuxième.
- si on obtient deux rouges, on gagne 6 euros
- si on obtient deux vertes , on gagne 3 euro
- sinon on on perd 1 euro.
On appelle X la variable aléatoire qui à une issue associe le gain algébrique en euros ( ne pas oublier la mise).
Déterminer la loi de probabilité de la variable aléatoire X.
Paramètres d’une variable aléatoire
Espérance, variance, écart-type
Définitions
X est une variable aléatoire réelle définie sur \Omega qui prend les valeurs a_1, a_2, a_3 , …a_n et dont la loi de probabilité est donnée ci-dessous
Valeur de X | a_1 | a_2 | … | a_n |
| P(X=a_i) | p_1 | p_2 | … | p_n |
L’espérance de la variable aléatoire X est le nombre réel noté E(X) défini par
E(X)=p_1a_1+p_2a_2+…+p_na_nLa variance de la variable aléatoire X est le nombre réel noté V(X) défini par
V(X)=p_1(a_1-E(X))^2+p_2(a_2-E(X))^2+…+p_n(a_n-E(X))^2L’écart-type de la variable aléatoire X est le nombre réel noté \sigma(X) défini par
\sigma(X)=\sqrt{V(X)}Exemple n°1 (suite et fin):
On lance un dé équilibré.
- si le numéro sorti est 2 ou 4, on gagne 2 euros,
- si le numéro sorti est impair on gagne 1 euro
- si le 6 sort, on perd 6 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Déterminer les paramètres de la variable aléatoire X.
Exemple n°2 (suite et fin) :
On lance deux fois de suite une pièce de monnaie.
- si on obtient deux fois pile, on gagne 2 euros
- si on obtient une seule fois pile , on gagne 1 euros
- sinon on perd 3 euros.
On appelle X la variable aléatoire qui à un numéro associe le gain algébrique en euros.
Déterminer les paramètres de la variable aléatoire X.
Exemple n°3 :
On mise 3 euros.
Ensuite on tire une première boule dans une urne qui contient deux rouges et trois vertes, on la remet dans l’urne et on en tire une deuxième.
- si on obtient deux rouges, on gagne 6 euros
- si on obtient deux vertes , on gagne 3 euro
- sinon on on perd 1 euro.
On appelle X la variable aléatoire qui à une issue associe le gain algébrique en euros ( ne pas oublier la mise).
Déterminer les paramètres de la variable aléatoire X.