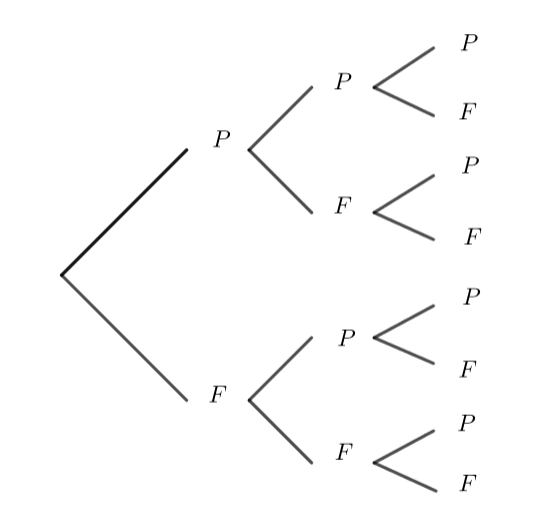
Exercice n°1
On vous propose le jeu suivant:
Pour jouer, il faut payer 2€. Ensuite, on lance 3 fois de suite une pièce bien équilibrée. Chaque pile rapporte 3€ et chaque face fait perdre 2€.
On considère la variable aléatoire G égale au gain algébrique du joueur. Déterminer la loi de probabilité de G et son espérance.
Exercice n°2
On lance deux dés cubiques bien équilibrés dont les faces sont numérotées de 1 à 6.
On note X la variable aléatoire égale à la somme des deux nombres sortis.
1) Déterminer la loi de probabilité de X.
2) Déterminer l’espérance de X.
Exercice n°3
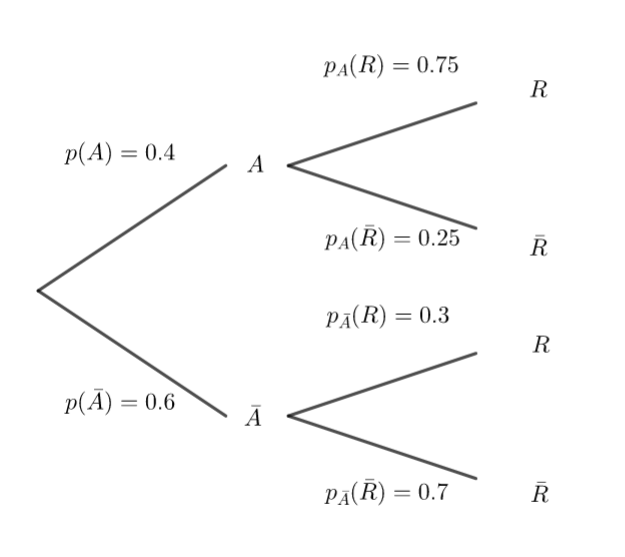
Deux vendeurs de bulbes de tulipes proposent des lots à la vente :
Dans les lots proposés par le premier vendeur 75 % des bulbes donnent des tulipes rouges et 25 % donnent des tulipes jaunes.
Dans les lots proposés par le second vendeur 30 % des bulbes donnent des tulipes rouges et 70 % donnent des tulipes jaunes.
Un fleuriste se fournit auprès de ces deux vendeurs. Il achète 40 % de ses bulbes de tulipes au premier vendeur et 60 % au deuxième.
On choisit au hasard un bulbe chez le fleuriste.
On note 𝐴 l’événement « Le bulbe provient du premier vendeur » et R l’événement « Le
bulbe donne des tulipes de couleur rouge ».
1.a. Recopier sur la copie et compléter l’arbre de probabilité ci-dessous :
b. Calculer p(A\cap R) et interpréter ce résultat.
c. Montrer que la probabilité que le bulbe soit de couleur rouge est 0.48.
d. Sachant que le bulbe choisi est rouge, quelle
est la probabilité qu’il ait été vendu par le deuxième vendeur ?
2. Le fleuriste fixe à 2 € le prix de vente d’un bulbe rouge et à 3 € le prix d’un bulbe jaune.
On choisit au hasard un bulbe chez le fleuriste et on désigne par 𝑋 la variable aléatoire égale
au prix en euros du bulbe acheté. Déterminer la loi de probabilité de 𝑋 puis son espérance.
Exercice n°4
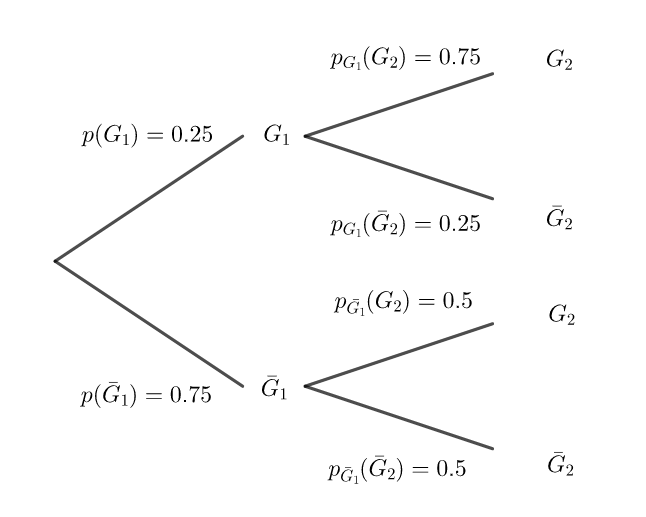
Un jeu se déroule en deux parties :
La probabilité que le joueur gagne la première partie est de 0,25
S’il gagne la première partie, il gagne la deuxième avec une probabilité de 0,75
S’il perd la première partie, il perd la suivante avec une probabilité de 0,5
On note :
G_1 l’événement « le joueur gagne la première partie »
G_2 l’événement « le joueur gagne la seconde partie »
1.a. Préciser p(G_1), p_{G_1}(G_2) et p_{\bar {G_1}}(\bar {G_2}) .
1.b.Construire un arbre pondéré illustrant la situation.
2. Calculer la probabilité que le joueur gagne les deux parties du jeu.
3. Montrer que la probabilité que le joueur gagne la deuxième partie du jeu est 0.5625 .
4. On sait de plus que :
à chaque partie gagnée, le joueur gagne 1,5 €.
à chaque partie perdue, il perd 1 €.
On note 𝑋 la variable aléatoire qui correspond au gain algébrique en euros de Maxime
à l’issue des deux parties.
a. Recopier sur la copie et compléter le tableau ci-dessous donnant la loi de
probabilité de la variable aléatoire 𝑋.
| a_i | |||
| p(X=a_i) |
b. Déterminer si ce jeu est équitable. Justifier