Définition
A et B sont deux évènements avec p(A)\ne 0.
La probabilité de l’évènement B sachant A est définie par p_A(B)=\frac{p(A\cap B)}{p(A)}.
Dans ce cas précis la condition est A, c’est cet évènement qui est écrit juste après le mot sachant.
Exercice n°1:
Dans un pays, il y a 2 % de la population contaminée par un virus.
On dispose d’un test de dépistage d’un virus qui a les propriétés suivantes :
– La probabilité qu’une personne contaminée ait un test positif est de 0,99 (sensibilité du test).
– La probabilité qu’une personne non contaminée ait un test négatif est de 0,97 (spécificité du
test).
On fait passer un test à une personne choisie au hasard dans cette population.
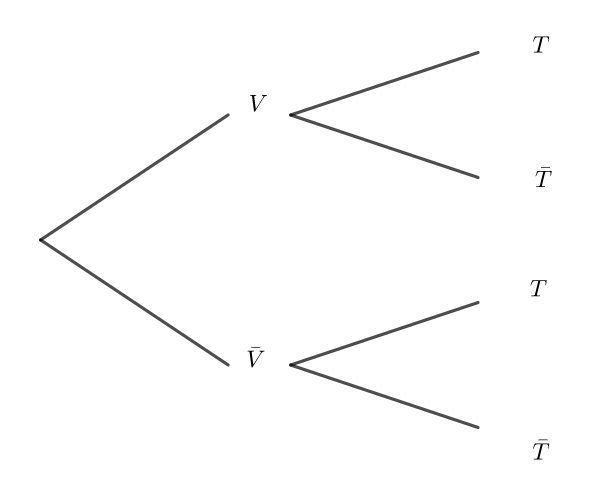
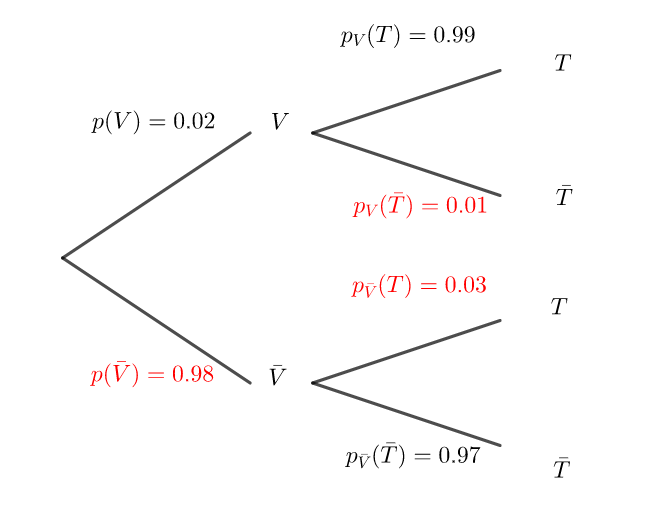
On note V l’évènement « la personne est contaminée par le virus » et T l’évènement « le test est positif ».
\bar{V}et \bar{T} désignent respectivement les évènements contraires de V et T .
Préciser les valeurs des probabilités p(V), p_V(T) et p_{\bar{V}}(\bar{T}) puis compléter l’arbre ci-dessous.
Propriété : Formule de Bayes
A et B sont deux évènements de probabilités non nulles.
On a:
p_B(A)\times p(B)=p_A(B)\times p(A).
Ou encore
p_B(A)=\frac{p_A(B)\times p(A)}{p(B)}.
Exercice n°2 :
Dans un aéroport, les portiques de sécurité servent à détecter les objets métalliques que peuvent
emporter les voyageurs.
On choisit au hasard un voyageur franchissant un portique.
On note :
S l’évènement « le voyageur fait sonner le portique »;
M l’évènement « le voyageur porte un objet métallique ».
On considère qu’un voyageur sur 500 porte sur lui un objet métallique.
1. On admet que :
Lorsqu’un voyageur franchit le portique avec un objet métallique, la probabilité que le
portique sonne est égale à 0,98;
Lorsqu’un voyageur franchit le portique sans objet métallique, la probabilité que le portique ne sonne pas est aussi égale à 0,98.
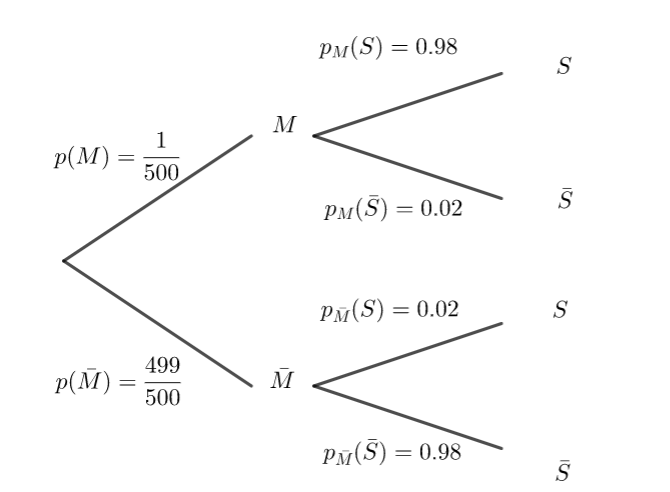
À l’aide des données de l’énoncé, préciser les valeurs de p(M), p_M(S)et p_{\bar{M}}(\bar{S})
2. Recopier et indiquer les probabilités sur les branches de l’arbre pondéré ci-dessous illustrant la situation.
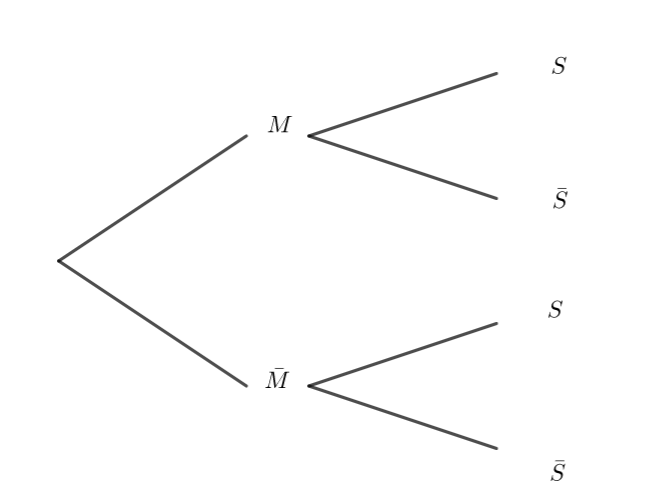
3. Montrer que : p(S)=0.02192.
4. A l’aide de la formule de Bayes, calculer la probabilité qu’un voyageur porte un objet métallique sachant qu’il a fait sonner le portique.
définition
Dire que deux évènements A et B sont indépendants signifie que p(A\cap B)={p(A)}\times{p(B)}.
Exercice n°3
A et B sont deux évènements d’un univers \Omega. p(A)=0.4 , p(B)=0.5 et p(A\cup B)=0.7
- Calculer p(A\cap B).
2. Les évènements A et B sont-ils incompatibles ?
3. Les évènements A et B sont-ils indépendants ?
Propriété :
– A et B sont indépendants si et seulement si p_A(B)=p(B)
– A et B sont indépendants si et seulement si p_B(A)=p(A)
Définition : Partition de l’univers
On considère un univers \Omega, on dit que \{A_1,A_2,…,A_n\} forme une partition de l’univers si les évènements sont disjoints deux à deux et si A_1\cup A_2\cup…\cup A_n=\Omega.
Propriété : Théorème des probabilités totales
On considère un univers \Omega et \{A_1,A_2,…,A_n\} une partition de l’univers. Pour tout évènement B de l’univers.
p(B)=p(A_1\cap B)+p(A_2\cap B)+…+p(A_n\cap B)Exercice n°4
Une entreprise de transports routiers dispose de 16 camions dont :
• 9 sont considérés comme « anciens »
• 4 sont considérés comme « récents »
• 3 sont considérés comme « neufs ».
L’entreprise décide d’observer l’état des 16 camions pendant une période donnée. On sait de plus
que, pendant cette période, la probabilité que :
• un camion « ancien » ait une panne, est égale à 0,08
• un camion « récent » ait une panne, est égale à 0,05
• un camion « neuf » ait une panne, est égale à 0,002 5.
On choisit au hasard un camion parmi les 16. On note les évènements suivants :
A : « le camion est ancien »
R : « le camion est récent »
N : « le camion est neuf »
D : « le camion a une panne ».
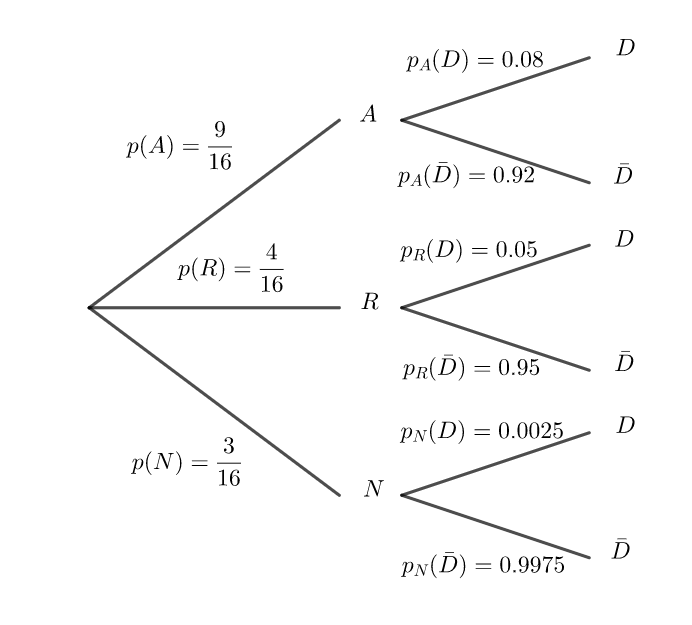
1. Reproduire et compléter l’arbre pondéré ci-dessous.
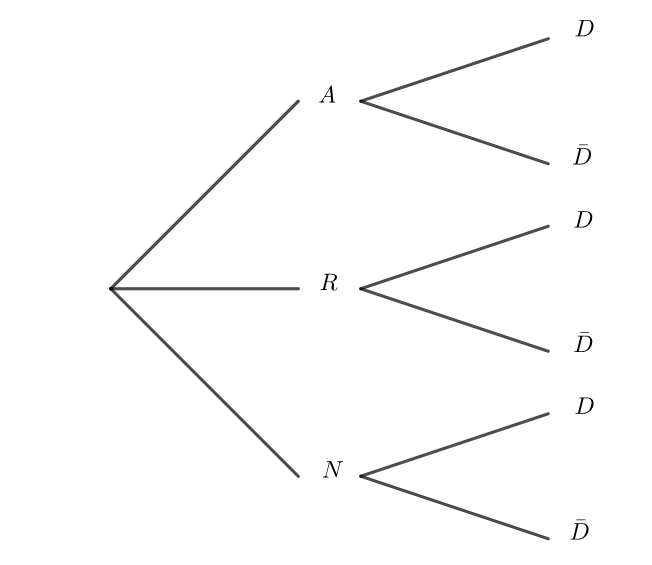
2. Calculer p(R\cap D).
3. A l’aide du théorème des probabilités totales calculer p(D)
4. A l’aide de la formule de Bayes, calculer la probabilité que le camion soit récent sachant qu’il a une panne.