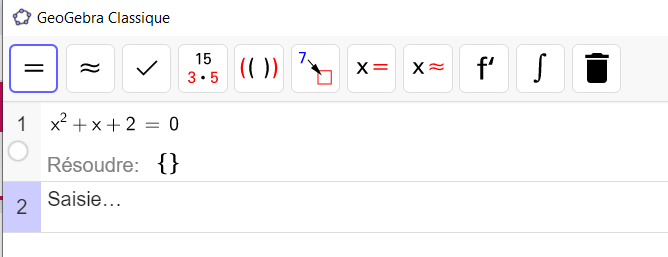
Résoudre dans \mathbf{R} l’équation : x^2+x+2=0
1.Conjecture graphique : déterminons, si c’est possible, la ou les abscisses du ou des point(s) d’intersection de la courbe de la fonction f définie par f(x)=x^2+x+2 et de l’axe des abscisses.
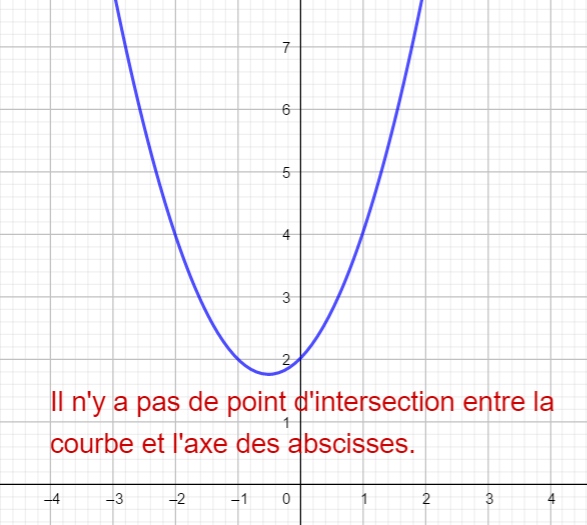
On conjecture donc graphiquement que l’équation x^2+x+2=0 n’admet pas de solution.
2. Résolution de l’équation x^2+x+2=0 par le calcul en utilisant le théorème du cours.
J’identifie les coefficients l’équation a=1, b=1 et c=2.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 1,1,2 .
\Delta=1²-4\times{1}\times{2}\\\Delta=1-8\\\Delta=-7comme \Delta<0 , l’équation n’admet pas de solution
Je conclus S=\emptyset
3. Vérifications éventuelles
a. A l’aide de la calculatrice TI-83 Premium CE EDITION PYTHON

b. A l’aide de l’application Calcul Formel de Géogébra.