Résoudre 1+4x+4x^2\geq 0
1.Conjecture graphique :
pour résoudre graphiquement 1+4x+4x^2\geq 0
Je traduis la question par une phrase en français:
Je cherche pour quelles valeurs de x la courbe de la fonction f est au dessus ou sur la droite d’équation y=0 ( c’est l’axe des abscisses)
où f est définie sur \mathbf{R} par f(x)=1+4x+4x^2.
Ensuite je parcours la courbe avec mon index de la gauche vers la droite en disant oui si la courbe de la fonction f est au dessus ou sur la droite d’équation y=0 et non dans le cas contraire.
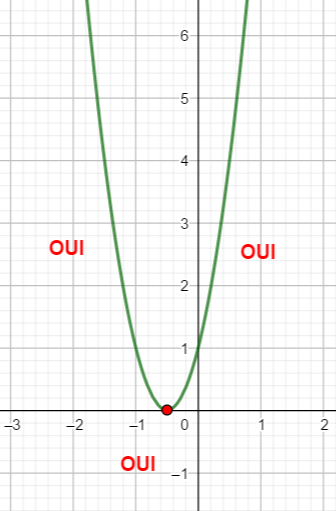
Je conclus S=\left[-1.8;0.8\right]
2.Résoudre 1+4x+4x^2\geq 0 par le calcul.
On ordonne le polynôme 4x^2+4x+1 \geq 0
Etape n°1 : Ecrire la phrase d’introduction.
Je cherche pour quelles valeurs de x le polynôme 4x^2+4x+1 est de signe positif (+) ou nul (0)
Etape n°2: Etude du signe de 4x^2+4x+1 par le calcul en utilisant le théorème vu dans la fiche 1.signe d’un polynôme du 2nd degré.
J’identifie les coefficients a=4, b=4 et c=1.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 4, 4, 1 .
\Delta=4²-4\times{4}\times{1}\\\Delta=16-16\\\Delta=0comme \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}
Je calcule x_0=-\frac{b}{2a} en remplaçant a,b par 4, 4.
x_0=-\frac{4}{2\times{4}}\\x_0=-\frac{1}{2}Je dresse le tableau de signes du polynôme:
Comme a=4 le signe de a est positif.

Etape n°3 : Je réponds à la question posée en lisant le tableau de signes
le polynôme 4x^2+4x+1 est de signe positif (+) ou nul (0) pour toutes les valeurs de x.
J’écris l’ensemble solution sous forme d’intervalle.
S=\left]-\infty;+\infty\right[.
3.Vérification avec l’application calcul Formel de géogébra




