Pendant la semaine du blanc, une grande surface a mis en vente un lit à 499 euros et une parure de draps à 49 euros.
On a constaté que
40% des clients du magasin ont acheté un lit .
Parmi les clients ayant acheté un lit, 70 % ont acheté une parure de draps
Parmi les clients du magasin n’ayant pas acheté de lit, 25 % ont tout de même acheté une parure de draps.
On choisit au hasard un client. On admet qu’un client achète au plus un lit et au plus une parure de draps.
On note les événements suivants :
L « le client achète un lit »
D « le client achète une parure de draps ».
1. Reproduire sur la copie et compléter l’arbre pondéré ci-dessous décrivant la situation.
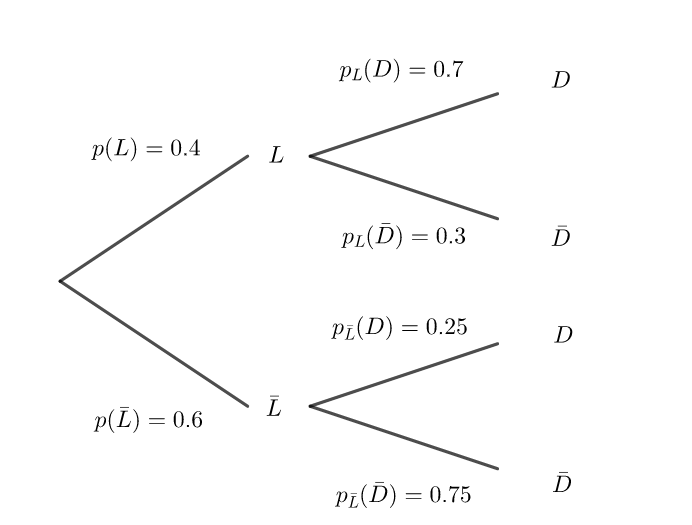
40% des clients du magasin ont acheté un lit donc p(L)=\frac{40}{100}=0.4
La somme des probabilités sur les branches issues d’un même noeud est toujours égale à 1.
p(\bar L)=1-p(L)=1-0.4=0.6
Parmi les clients ayant acheté un lit, 70 % ont acheté une parure de draps
On peut reformuler
Sachant que la personne a acheté un lit, la probabilité qu’elle achète une parure de draps est \frac{70}{100}
p_L(D)=\frac{70}{100}=0.7La somme des probabilités sur les branches issues d’un même noeud est toujours égale à 1.
p_L(\bar D)=1-0.7=0.3
Parmi les clients du magasin n’ayant pas acheté de lit, 25 % ont tout de même acheté une parure de draps.
On peut reformuler
Sachant que la personne n’a pas acheté de lit, la probabilité qu’elle achète une parure de draps est \frac{25}{100}
p_{\bar L}(D)=\frac{25}{100}=0.25La somme des probabilités sur les branches issues d’un même noeud est toujours égale à 1.
p_{\bar L}(\bar D)=1-0.25=0.75
2. Calculer la probabilité que le client achète un lit et une parure de draps.
Pour calculer p(L\cap D), on calcule la probabilité du chemin qui passe pas L et D en faisant le produit des probabilités sur les branches. Ce qui revient à appliquer la formule du cours p(L\cap D)=p(L)\times p_L(D).
p(L\cap D)=p(L)\times p_L(D).
p(L\cap D)=0.4\times 0.7.
p(L\cap D)=0.28.

3. Montrer que la probabilité de l’événement D est égale à 0.43.
Pour calculer p( D), on ajoute les probabilités de tous les chemins qui mènent à D. Ce qui revient à appliquer la formule des probabilités totales
p(D)=p(L\cap D)+p(\bar L\cap D).
p(D)=p(L\cap D)+p(\bar L\cap D)p(D)=0.28+p(\bar L)\times p_{\bar L}(D).
p(D)=0.28+0.6\times 0.25.
p(D)=0.28+0.15.
p(D)=0.43.

4. Calculer la probabilité que le client achète un lit sachant qu’il a acheté une parure de draps.
Il faut calculer la probabilité que le client achète un lit sachant qu’il a acheté une parure de draps.
Pour calculer p_D( L), on ne peut pas utiliser l’arbre car pour l’arbre la condition est L ou \bar L. On applique donc la formule du cours.
p_D(L)=\frac{p(L\cap D)}{p(D)}
p_D(L)=\frac{p(L\cap D)}{p(D)}\\p_D(L)=\frac{0.28}{0.48}\\p_D(L)=0.585. On appelle S la variable aléatoire donnant la somme dépensée par un client au rayon literie.
Calculer l’espérance mathématique de 𝐷 et donner une interprétation de ce nombre dans le contexte de l’exercice.
Pendant la semaine du blanc, une grande surface a mis en vente un lit à 499 euros et une parure de draps à 49 euros.
On appelle S la variable aléatoire donnant la somme dépensée par un client au rayon literie.
Tout d’abord, on cherche les valeurs réelles prises par la variable aléatoire S. Les valeurs sont
0 , 49 , 499 et 548.
Je prépare le tableau de la loi de probabilité.
| a_i | 0 | 49 | 499 | 548 |
| p(S=a_i) |
On va utiliser l’arbre.
L’évènement la somme dépensée est 0 est composée de l’issue \bar L\cap \bar D
p(S=0)=p(\bar L\cap \bar D)\\p(S=0)=0.6\times 0.75=0.45L’évènement la somme dépensée est 49 est composée de l’issue \bar L\cap D
p(S=49)=p(\bar L\cap D)\\p(S=49)=0.6\times 0.25=0.15L’évènement la somme dépensée est 499 est composée de l’issue L\cap \bar D
p(S=499)=p(L\cap \bar D)\\p(S=499)=0.4\times 0.3=0.12L’évènement la somme dépensée est 548 est composée de l’issue L\cap D
p(S=548)=p(L\cap D)\\p(S=548)=0.4\times 0.7=0.28

| a_i | 0 | 49 | 499 | 548 |
| p(S=a_i) | p(S=0)=0.45 | p(S=49)=0.15 | p(S=499)=0.12 | p(S=548)=0.28 |
On calcule l’espérance
E(x)=0\times0.45+49\times0.15+499\times0.12+548\times0.28\\E(x)=220.67Sur un grand nombre d’acheteurs, la dépense sera en moyenne 221 euros.



