Définition
Une épreuve de Bernoulli est une expérience à deux issues.
L’ une est appelée succès et notée S et l’autre est appelée échec et est notée \bar S.
Exemples
- Jeter une pièce de monnaie est une épreuve de Bernoulli où le succès pourrait être obtenir pile et l’échec obtenir face. Ici p(S)=\frac{1}{2} et p(\bar S)=\frac{1}{2}
- Jeter un dé à six faces peut-être une épreuve de Bernoulli si on prend pour le succès S : obtenir un six et pour l’échec \bar S : ne pas obtenir un six. Ici p(S)=\frac{1}{6} et p(\bar S)=\frac{5}{6}.
- Choisir une carte dans un jeu de 32 cartes peut être une épreuve de Bernoulli si on prend pour le succès S : obtenir un as et pour l’échec \bar S : ne pas obtenir un as. Ici p(S)=\frac{4}{32} et p(\bar S)=\frac{28}{32}.
Définition
On considère une épreuve de Bernoulli où la probabilité du succès est p.
X est la variable aléatoire qui prend la valeur 1 en cas de succès et qui prend la valeur 0 en cas d’échec.
La loi de probabilité présentée ci-dessous est appelée loi de Bernoulli de paramètre p.
a_i | 0 | 1 |
| p(X=a_i) | 1-p | p |
Exemples
- On jette une pièce de monnaie ,si le succès est: obtenir face, la variable aléatoire X qui vaut 1 en cas de succès et 0 en cas d’échec suit une loi de Bernoulli de paramètre 0.5.
- On jette un dé à six faces ,si le succès est: obtenir un six, la variable aléatoire X qui vaut 1 en cas de succès et 0 en cas d’échec suit une loi de Bernoulli de paramètre \frac{1}{6}.
- On choisit une carte dans un jeu de 32 ,si le succès est: obtenir un as, la variable aléatoire X qui vaut 1 en cas de succès et 0 en cas d’échec suit une loi de Bernoulli de paramètre \frac{4}{32} ou \frac{1}{8}
Propriété
Soit X une variable aléatoire qui suit la loi de Bernoulli de paramètre p alors
- l’espérance de Xest E(X)=p
- la variance de Xest V(X)=p(1-p)
- l’écart-type de Xest \sigma(X)=\sqrt{p(1-p)}
Exercice n°1
Dans chaque cas, dire si la variable aléatoire X suit ou non une loi de Bernoulli. Si oui, préciser p,E(X), V(X),\sigma(X) .
1) On lance un dé équilibré. X prend la valeur qui correspond au nombre qu’on lit sur la face supérieure.
2) On tire une carte dans un jeu de 32 cartes, X prend la valeur 1 si on tire une figure ( roi, dame ou valet) et X prend la valeur 0 sinon.
3) On lance une pièce de monnaie équilibrée, X prend la valeur 1 si on obtient face et X prend la valeur 0 si on obtient pile.
4) Dans une entreprise 25% des employés viennent travailler à pied, 25% % des employés viennent travailler à vélo et 50%% des employés viennent travailler en voiture.
X prend la valeur 1 si l’employé vient travailler à pied et X prend la valeur 0 sinon.
Définition
L’ expérience aléatoire consistant à répéter n fois de manière indépendante une épreuve de Bernoulli de paramètre p s’appelle un schéma de Bernoulli de paramètres n et p.
Exemples :
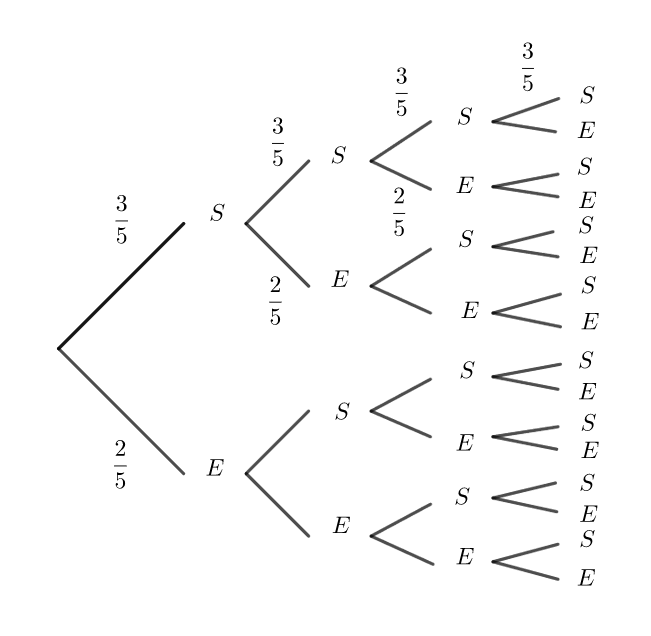
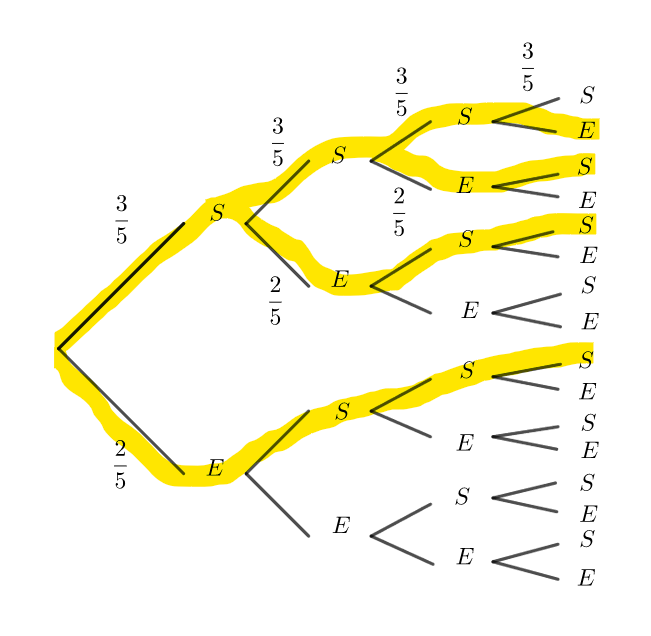
- On lance une pièce de monnaie trois fois de suite. Le succès est : obtenir face.
C’est un schéma de Bernoulli de paramètres 3 et \frac{1}{2}.
- On lance un dé quatre fois de suite. Le succès est : obtenir un 6.
C’est un schéma de Bernoulli de paramètres 4 et \frac{1}{6}.
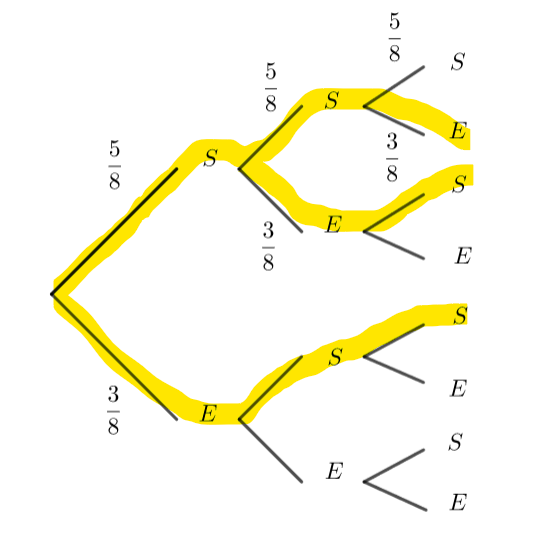
- On tire successivement avec remise une boule dans une urne qui contient 2 boules rouges et trois noires, trois fois de suite. Le succès est de tirer une boule rouge.
C’est un schéma de Bernoulli de paramètres 3 et \frac{2}{5}.
Définition
Soit n un entier naturel non nul et k un entier compris entre 0 et n.
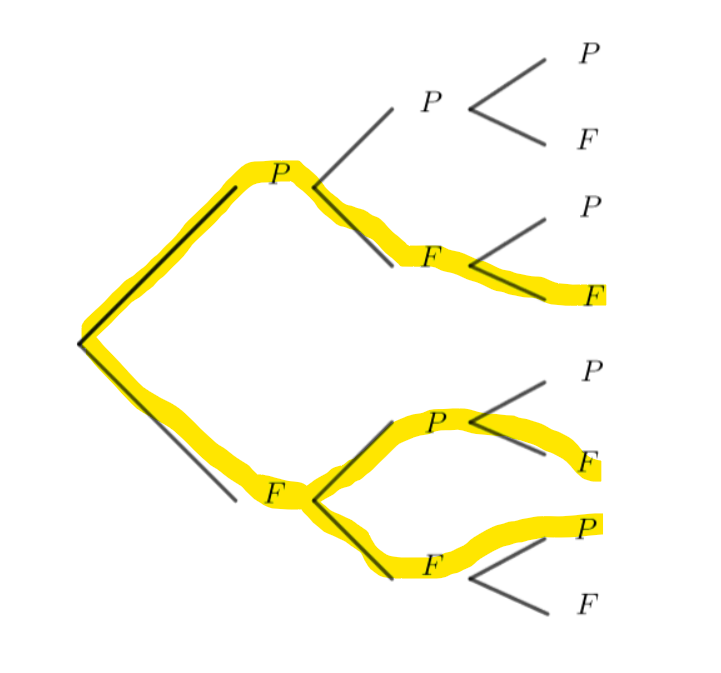
Le coefficient binomial \binom{n}{k} est le nombre de chemins réalisant k succès pour n répétitions sur l’arbre associé à un schéma de Bernoulli.
Par convention : \binom{0}{0}=1.
Conséquence
Compléter les pointillés.
\binom{n}{0}=… \binom{n}{1}=… \binom{n}{n}=…
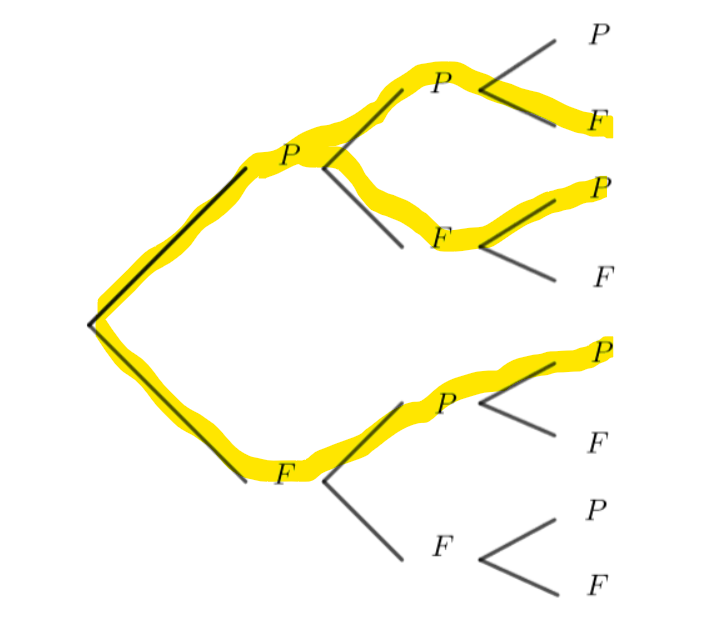
Exercice n°2
On jette une pièce de monnaie trois fois de suite. On appelle succès : obtenir face. A l’aide de l’arbre ci-dessous et à l’aide de la définition déterminer les coefficients binomiaux dans chaque cas.
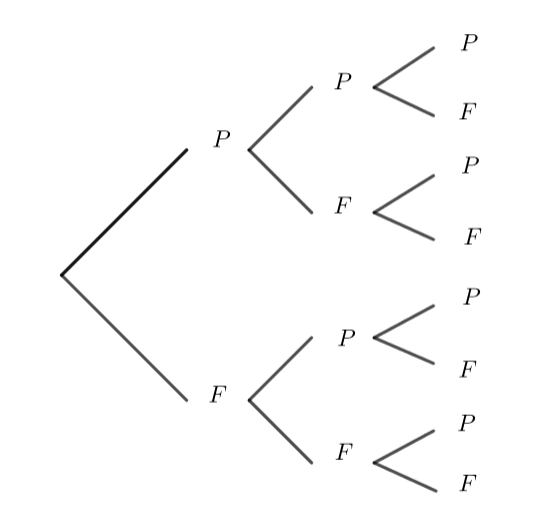
- \binom{3}{1}=…
2. \binom{3}{2}=…
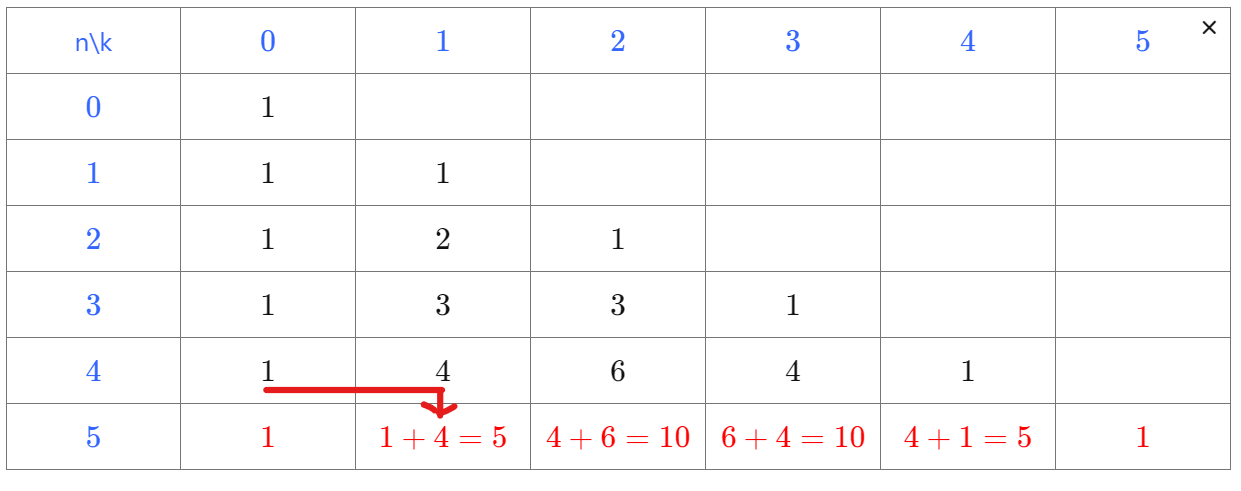
Calcul de coefficients binomiaux à l’aide du triangle de Pascal
Après avoir observé, remplir la dernière ligne.
| n\k | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | |||||
| 1 | 1 | 1 | ||||
| 2 | 1 | 2 | 1 | |||
| 3 | 1 | 3 | 3 | 1 | ||
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 |
Propriétés
Soit n un entier naturel non nul et k un entier compris entre 0 et n-1.
\binom{n}{k}+\binom{n}{k+1}=\binom{n+1}{k+1}Pour tout entier k compris entre 0 et n.
\binom{n}{k}=\binom{n}{n-k}Exercice n°3
On tire successivement trois cartes avec remise dans un jeu de 32 cartes.
On compte le nombre de figures obtenues dans le tirage.
On note S le succès obtenir une carte qui ne soit pas une figure.
- Modéliser la situation par un arbre de probabilités, indiquer les probabilités sur quelques branches.
2. Cette expérience constitue-t-elle un schéma de Bernoulli ? Si oui, préciser ses paramètres.
3. Déterminer la probabilité qu’exactement deux cartes ne soient pas des figures.
Exercice n°4
On tire successivement quatre boules avec remise dans une urne qui contient six boules vertes et quatre boules rouges.
On compte le nombre de boules vertes obtenues dans le tirage.
- Expliquer pourquoi on peut modéliser cette expérience par un schéma de Bernoulli, puis préciser les valeurs des paramètres n et p.
2. Représenter ce schéma de Bernoulli par un arbre pondéré en portant quelques probabilités sur les branches.
3. Déterminer la probabilité qu’exactement trois boules soient vertes.