logo

Exercice de synthèse sur les vecteurs

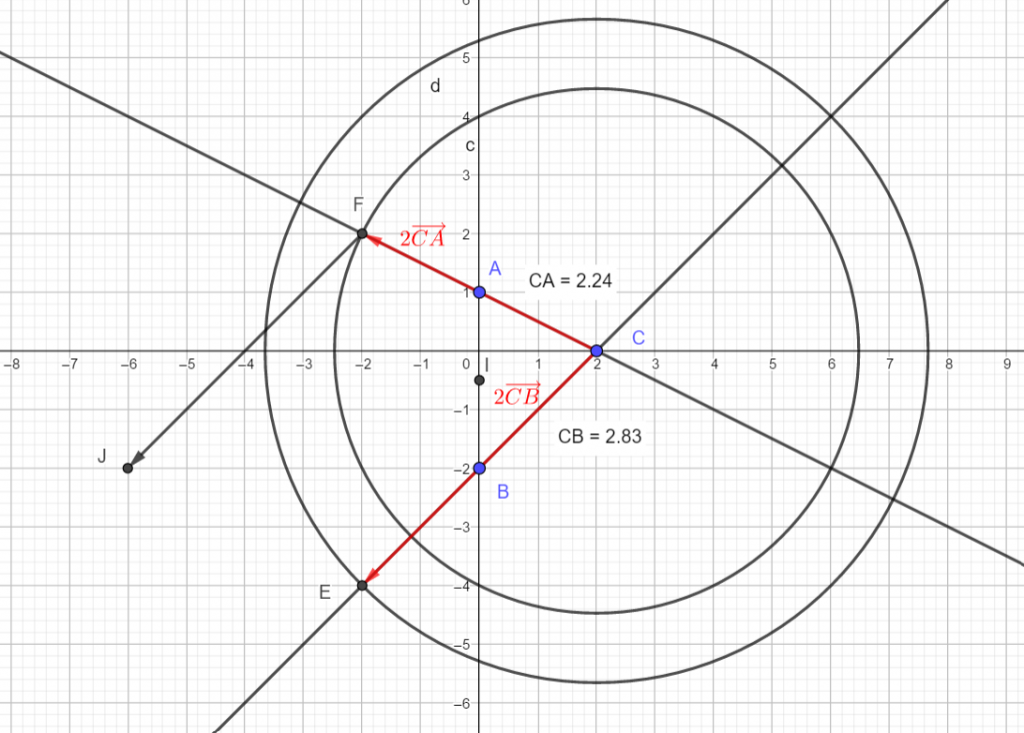
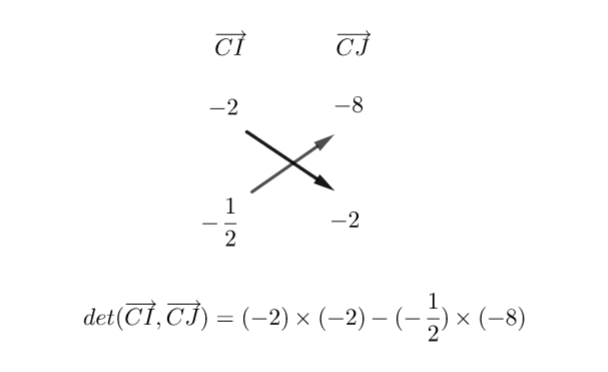 SoientA(0;1), B(0;-2), C(2;0) trois points du plan.

On note I le milieu du segment [AB].

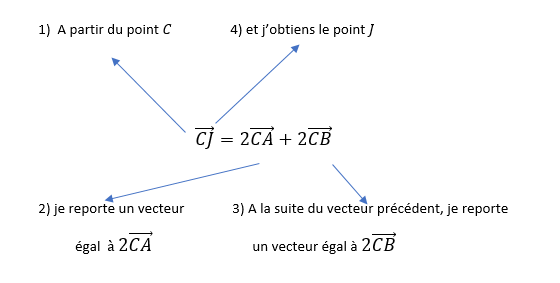
Le point J est défini par l’égalité vectorielle suivante: \overrightarrow{CJ}=2\overrightarrow{CA}+2\overrightarrow{CB}

  1. Placer les points I et J dans le repère ci-dessus. Puis conjecturer graphiquement leurs coordonnées.
correction

2. Calculer les coordonnées du point I(on ne peut pas utiliser le résultat de la question précédente).

correction

3. Calculer les coordonnées du point J(on ne peut pas utiliser le résultat de la question n°2).

correction

4.a. Calculer les coordonnées du vecteur \overrightarrow{CI}.

correction

4.b. Calculer les coordonnées du vecteur \overrightarrow{CJ}.

correction

4.c. Calculer le déterminant des vecteurs \overrightarrow{CI} et \overrightarrow{CJ}. Qu’en déduire pour les vecteurs \overrightarrow{CI} et \overrightarrow{CJ}? Puis qu’en déduire pour les points C , I et J ?

correction

©2020 – Math’O karé SAS

  1. Construire le point I le milieu de [AB].

Avec Géogébra cliquer gauche sur le 2ème onglet en partant de la gauche et sélectionner Milieu ou centre dans le menu déroulant. Dans le repère cliquer gauche sur le point A  et sur le point B . Cliquer droit sur le milieu, sélectionner Renommer dans le menu déroulant et appeler le point I.

2. Pour construire le point J défini par l’égalité vectorielle \overrightarrow{CJ}=2\overrightarrow{CA}+2\overrightarrow{CB} 

  1. A partir de C, je reporte un vecteur égal à 2\overrightarrow{CA}

Avec Géogébra cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point A  et sur le point C . 

Puis cliquer gauche sur le 8ème onglet en partant de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer gauche sur le point  A  et sur le point C . 

Enfin cliquer gauche sur le 6ème onglet en partant de la gauche et sélectionner Cercle ( centre-rayon) dans le menu déroulant.

Dans le repère cliquer gauche sur le point  C  et écrire  2CA dans la case Rayon .

Construire le vecteur égal à 2\overrightarrow{CA}et nommer F son extrémité.

2. A la suite du vecteur tracé précédemment, je reporte un vecteur égal à 2\overrightarrow{CB}

a) je construis le vecteur 2\overrightarrow{CB}

Avec Géogébra cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point  C  et sur le point B .

Puis cliquer gauche sur le 8ème onglet en partant de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer gauche sur le point C  et sur le point B . 

Enfin cliquer gauche sur le 6ème onglet en partant de la gauche et sélectionner Cercle ( centre-rayon) dans le menu déroulant.

Dans le repère cliquer gauche sur le point  C  et écrire  2CB dans la case Rayon .

Construire le vecteur égal à 2\overrightarrow{CB}

b) je construis un représentant du vecteur 2\overrightarrow{CB} à la suite du vecteur 2\overrightarrow{CA}

Enfin cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Représentant dans le menu déroulant.

Dans le repère cliquer gauche sur F l’extrémité du vecteur 2\overrightarrow{CA}et sur le vecteur 2\overrightarrow{CB}.

On obtient alors le point J .

Par lecture graphique, I(0;-0.5) et J(-6;-2)  .

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(0;1) \hspace{0.4cm} B(0;-2)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {0+0}{2}\hspace {2cm}y_I=\frac {1+(-2)}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (1-2)/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez 1-2/2, vous obtiendrez 0 car la machine calculera 2/2 en priorité ce qui est faux

x_I=0\hspace {2cm}y_I=-\frac {1}{2}

Donc I(0;-\frac {1}{2})

On veut déterminer les coordonnées du point J tel que \overrightarrow{CJ}=2\overrightarrow{CA}+2\overrightarrow{CB}.

Comme on le les connaît pas, on les appelle x et y. 

On pose  J(x;y).

Les vecteurs \overrightarrow{CJ} et 2\overrightarrow{CA}+2\overrightarrow{CB} sont égaux donc leurs coordonnées sont égales.

Tâche n°1 : Je calcule les coordonnées de \overrightarrow{CJ} . Puis je calcule les coordonnées de \overrightarrow{CA} et ensuite de 2\overrightarrow{CA}. Ensuite je calcule les coordonnées de \overrightarrow{CB} et ensuite de 2\overrightarrow{CB}. Et enfin les coordonnées de 2\overrightarrow{CA}+2\overrightarrow{CB}

Pour déterminer les coordonnées du vecteur \overrightarrow{CJ}.

Je repère les coordonnées des points C et J.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.4cm}x_{J}\hspace{0.2cm}y_{J}

\hspace{1.8cm}C(2;0)\hspace{0.2cm}J(x;y)

J’écris la formule : \overrightarrow{CJ}(x_{J}-x_{C};y_{J}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CJ}(x-2;y-0)

\overrightarrow{CJ}(x-2;y)

Pour déterminer les coordonnées du vecteur \overrightarrow{CA}.

Je repère les coordonnées des points C et A.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.6cm}x_{A}\hspace{0.2cm}y_{A}

\hspace{1.8cm}C(2;0)\hspace{0.2cm}A(0;1)

J’écris la formule : \overrightarrow{CA}(x_{A}-x_{C};y_{A}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CA}(0-2;1-0)

\overrightarrow{CA}(-2;1)

Pour obtenir les coordonnées du vecteur 2\overrightarrow{CA}, je dois multiplier le coordonnées du vecteur \overrightarrow{CA} par 2

2\overrightarrow{CA}({2}\times{(-2)};{2}\times{1})\\2\overrightarrow{CA}(-4;2)

Pour déterminer les coordonnées du vecteur \overrightarrow{CB}.

Je repère les coordonnées des points C et B.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.6cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}C(2;0)\hspace{0.2cm}B(0;-2)

J’écris la formule : \overrightarrow{CB}(x_{B}-x_{C};y_{B}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CB}(0-2;(-2)-0)

\overrightarrow{CB}(-2;-2)

Pour obtenir les coordonnées du vecteur 2\overrightarrow{CB}, je dois multiplier le coordonnées du vecteur \overrightarrow{CB} par 2

2\overrightarrow{CB}({2}\times{(-2)};{2}\times{(-2)})\\2\overrightarrow{CB}(-4;-4)

Enfin

2\overrightarrow{CA}+2\overrightarrow{CB}((-4)+(-4);2+(-4))\\2\overrightarrow{CA}+2\overrightarrow{CB}(-8;-2)

Tâche n°2 : J’écris que les coordonnées de \overrightarrow{CJ}et  de 2\overrightarrow{CA}+2\overrightarrow{CB} sont égales pour obtenir deux équations du premier degré.

L’abscisse de \overrightarrow{CJ}=l’abscisse de 2\overrightarrow{CA}+2\overrightarrow{CB}

x-2=-8

-2 n’est pas à sa place à gauche, j’ajoute 2 de chaque côté.

x=-8+2\\x=-6

L’ordonnée de \overrightarrow{CJ}=l’ordonnée de 2\overrightarrow{CA}+2\overrightarrow{CB}

y=-2

Donc J(-6;-2)

Pour déterminer les coordonnées du vecteur \overrightarrow{CI}.

Je repère les coordonnées des points C et I.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.6cm}x_{I}\hspace{0.2cm}y_{I}

\hspace{1.8cm}C(2;0)\hspace{0.4cm}I(0;-\frac{1}{2})

J’écris la formule : \overrightarrow{CI}(x_{I}-x_{C};y_{I}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CI}(0-2;(-\frac{1}{2})-0)

\overrightarrow{CI}(-2;-\frac{1}{2})

Pour déterminer les coordonnées du vecteur \overrightarrow{CJ}.

Je repère les coordonnées des points C et J.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.9cm}x_{J}\hspace{0.2cm}y_{J}

\hspace{1.8cm}C(2;0)\hspace{0.4cm}J(-6;-2)

J’écris la formule : \overrightarrow{CJ}(x_{J}-x_{C};y_{J}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CJ}((-6)-2;(-2)-0)

\overrightarrow{CJ}(-8;-2)

Pour calculer le déterminant des vecteurs \overrightarrow{CI} et \overrightarrow{CJ}, on utilise la disposition pratique suivante :

det(\overrightarrow{CI};\overrightarrow{CJ})=4-\frac{8}{2}\\det(\overrightarrow{CI};\overrightarrow{CJ})=4-4\\det(\overrightarrow{CI};\overrightarrow{CJ})=0

donc les vecteurs \overrightarrow{CI} et \overrightarrow{CJ} sont colinéaires.

donc les points C , I et  J sont alignés.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.