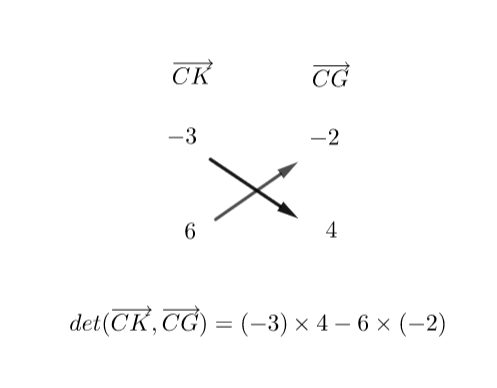Soient A(-2;3), B(-8;-1), C(-2;-5) trois points du plan. On s’intéresse au triangle ABC et à son centre de gravité G.
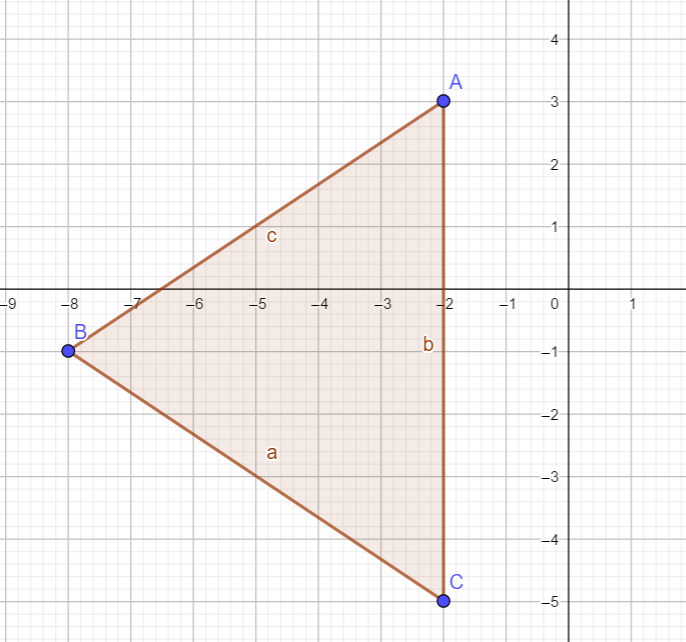
- Construire le triangle ABC le repère ci-dessous. On complètera la figure au fur et à mesure.
Pour placer A, cliquer gauche sur le deuxième onglet en haut à gauche , sélectionner Point dans le menu déroulant puis cliquer gauche dans le repère au point de coordonnées (-2;3) . Procéder de même pour les points B et C.
Pour tracer le triangle ABC, cliquer gauche sur le cinquième onglet en haut à gauche , sélectionner Polygone dans le menu déroulant puis cliquer gauche dans le repère sur le point A, le point B, le point C et à nouveau sur le point A.
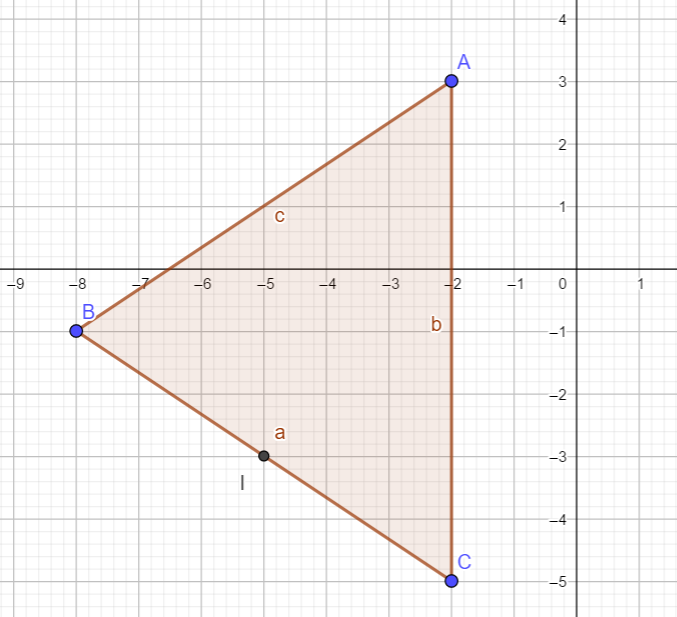
2. a. Déterminer par le calcul les coordonnées du milieu de [BC] qu’on appelera I.
Pour placer I, cliquer gauche sur le deuxième onglet en haut à gauche , sélectionner Milieu ou centre dans le menu déroulant puis cliquer gauche dans le repère sur le point B et sur le point C.
Le logiciel le nomme D, cliquer droit sur ce point et sélectionner Renommer dans le menu déroulant puis l’appeler I.
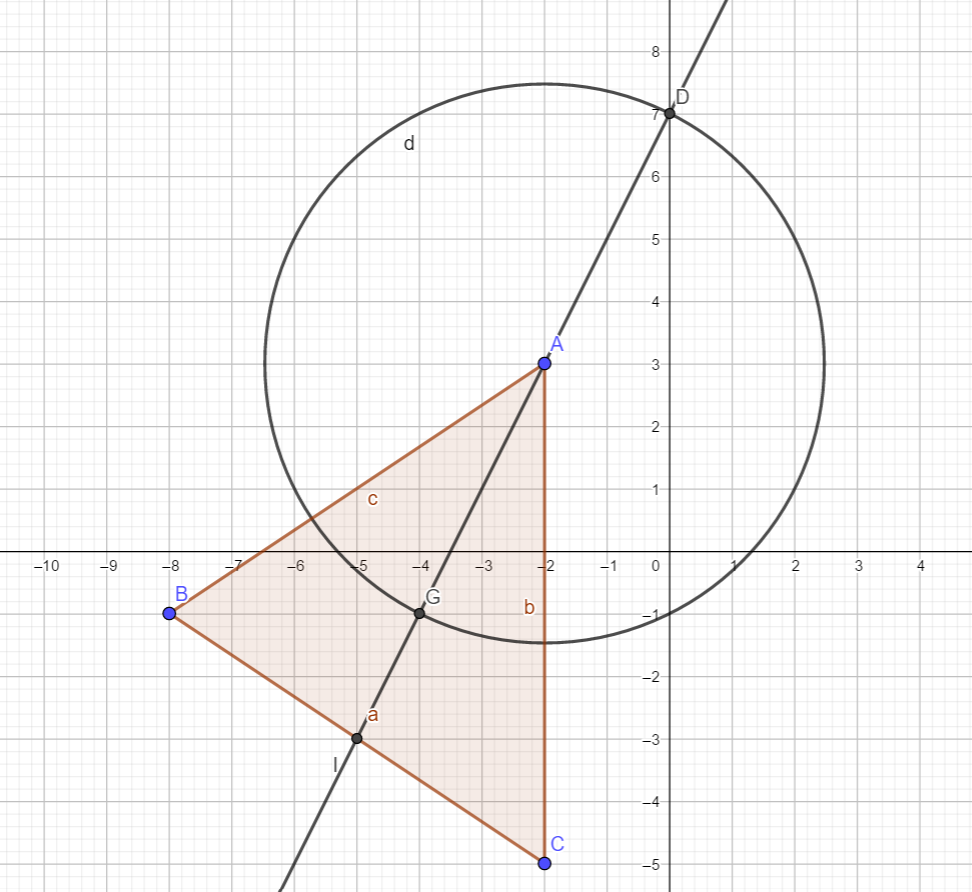
2. b. Déterminer par le calcul les coordonnées du point G défini par l’égalité vectorielle suivante : \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AI}.
Pour construire le point G défini par l’égalité vectorielle \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AI}
Cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point A et sur le point I .
Cliquer gauche sur le 6ème onglet en partant de la gauche et sélectionner Cercle ( centre-rayon) dans le menu déroulant.
Dans le repère cliquer gauche sur le point A et écrire 2AI/3 dans la case Rayon .
On choisit ensuite le point d’intersection du cercle et de la droite pour lequel \overrightarrow{AG} et \overrightarrow{AI} ont même sens car \frac{2}{3} est positif.
J’obtiens alors le point G.
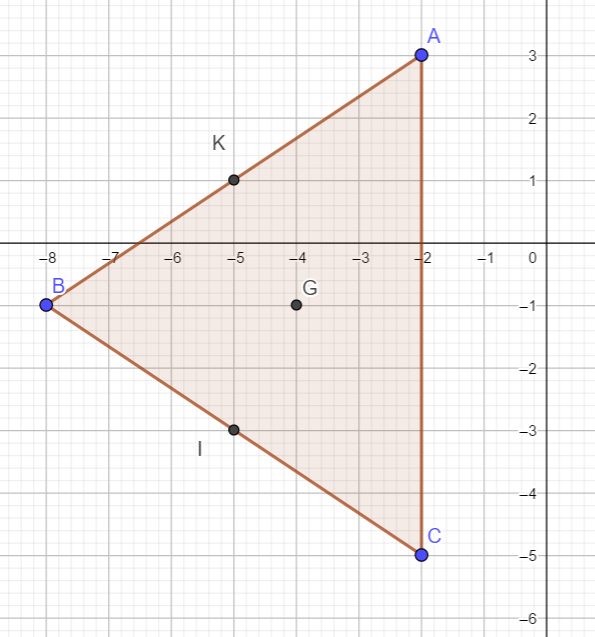
3. a. Déterminer par le calcul les coordonnées du milieu de [AB] qu’on appelera K.
Pour placer K, cliquer gauche sur le deuxième onglet en haut à gauche , sélectionner Milieu ou centre dans le menu déroulant puis cliquer gauche dans le repère sur le point A et sur le point B.
Le logiciel le nomme E, cliquer droit sur ce point et sélectionner Renommer dans le menu déroulant puis l’appeler K.
3.b. Montrer que les points C,K,G sont alignés.
Cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point C et sur le point K. S’assurer que cette droite passe par G.
4. Montrer par le calcul que \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}.