logo

Exercice-type évaluation fin d’année sur les fonctions.

Partie A
On considère la fonction polynôme du second degré g définie sur \mathbf{R} par :
g(x)=x^2-5x+4
1) Résoudre l’équation g(x)=0.

Utiliser la page de Calcul formel ci-dessous de Géogébra pour résoudre l’équation.

Saisir  x^2-5x+4=0 sur la ligne n°1 et cliquer sur le septième onglet X=. Géogébra affiche alors les solutions de l’équation.

correction

2) Étudier le signe de g  sur \mathbf{R}.

Utiliser la page de Calcul formel ci-dessus de Géogébra pour, par exemple, chercher quand g(x) est positif en résolvant l’inéquation g(x)>0.

Saisir  x^2-5x+4>0 sur la ligne n°1 et cliquer sur le septième onglet X=. Géogébra affiche alors les solutions de l’inéquation. Pour les autres valeurs de x, g(x) sera négatif.

correction

Partie B
On considère la fonction polynôme du troisième degré f définie sur \mathbf{R}par :
f(x)=2x^3-15x^2+24x
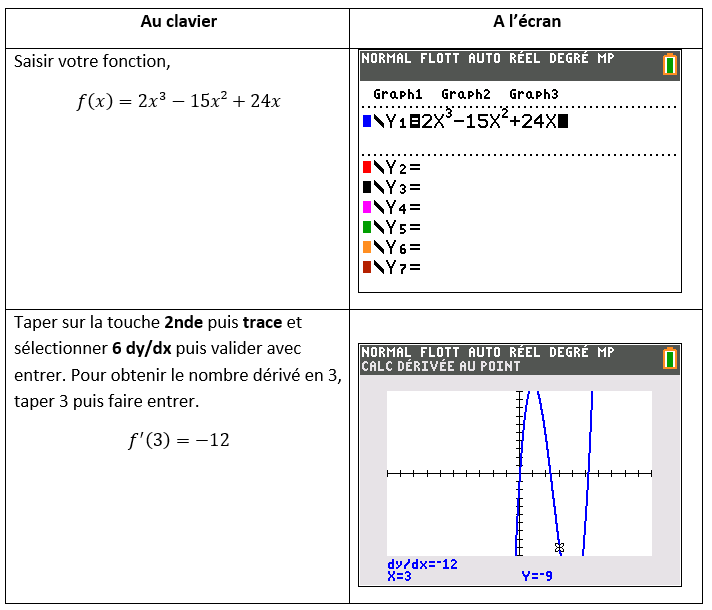
1) Calculer la dérivée f’ de f et vérifier que f'(x)=6g(x).

Utiliser la page de Calcul formel ci-dessus de Géogébra pour calculer f'(x).

Saisir  f(x)=2x^3-15x^2+24x sur la ligne n°1 et cliquer sur le neuvième onglet f’. Géogébra affiche alors la fonction dérivée. 

correction calcul de f'(x)
correction de f'(x)=6g(x)

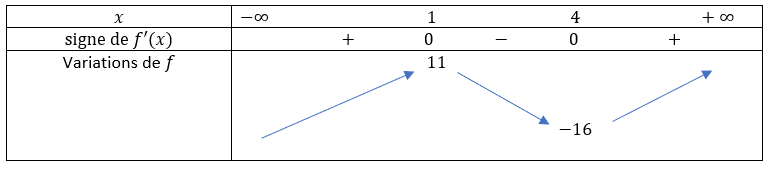
2) Etudier les variations de la fonction f.

correction

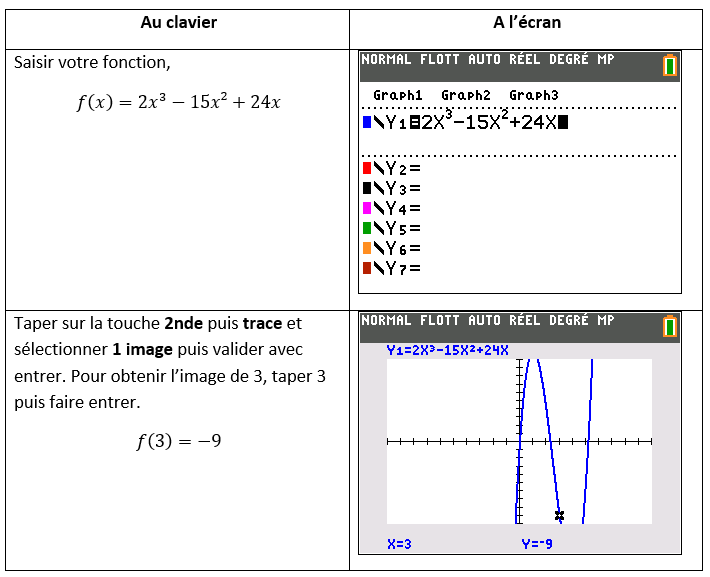
3) Déterminer une équation de la tangente T à la courbe représentative de f au point B d’abscisse 3.

Utiliser la page Géogébra ci-dessous.

Tracer la courbe de la fonction f.

Saisir dans la colonne de gauche, f(x)=2x^3-15x^2+24x 

Placer le point B.

Cliquer sur le deuxième onglet et sélectionner Point sur objet dans le menu déroulant. Dans le repère cliquer sur la courbe au point d’abscisse 3. Vous pouvez modifier l’affichage en cliquant sur le dernier onglet en haut à droite.

Tracer la tangente.

Cliquer sur le quatrième onglet et sélectionner Tangentes dans le menu déroulant. Dans le repère cliquer sur la courbe et sur le point d’abscisse 3. Le logiciel trace la tangente et son équation apparaît dans la colonne de gauche.

correction

©2020 – Math’O karé SAS

  L’équation g(x)=0 c’est-à-dire x^2-5x+4=0 est de la forme ax^2+bx+c=0

J’identifie les coefficients l’équation a=1, b=-5 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-5),4.

\Delta=(-5)²-4\times{1}\times{4}\\\Delta=25-16\\\Delta=9

comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-5)  , 9.

x_1=\frac{-(-5)-\sqrt{9}}{2\times{1}}\\x_1=\frac{5-3}{2}\\x_1=\frac{2}{2}\\x_1=1

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-5)  , 9.

x_2=\frac{-(-5)+\sqrt{9}}{2\times{1}}\\x_2=\frac{5+3}{2}\\x_2=\frac{8}{2}\\x_2=4

Je conclus S=\{1;4\}

 

Pour déterminer le signe de g(x) qui est une fonction polynôme, on utilise ce qui a été fait précédemment.

On a vu que \Delta= 9 donc il est positif et g(x) est donc du signe de a à l’extérieur des racines 1 et 4 et du signe de -a à l’intérieur.

Comme a=1, il est positif et voici le tableau de signes

f(x)= 2x^3-15x^2+24x pour x\in \mathbf{R}

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de trois termes :

2x^3 , -15x^2 et 24x.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Il faut donc calculer les dérivées des trois termes 2x^3 , -15x^2 et 24x en utilisant le deuxième tableau et le cas échéant le premier tableau.

Je calcule la dérivée de 2x^3 

C’est le produit de la constante 2 par la fonction cube x^3. J’utilise la deuxième ligne du premier tableau.

(2x^3)’=2(x^3)’

C’est une fonction de référence, j‘utilise la ligne cube du deuxième tableau.

(2x^3)’=2\times3x^2

(2x^3)’=6x^2

Je calcule la dérivée de -15x^2 .

C’est le produit de la constante -15 par la fonction carré x^2. J’utilise la deuxième ligne du premier tableau.

(-15x^2)’=-15\times (x^2)’

C’est une fonction de référence, j‘utilise la ligne carré du deuxième tableau.

\hspace{0.9cm}=-15\times 2x

\hspace{0.9cm}=-30x

Je calcule la dérivée de 24x .

C’est le produit de la constante 24 par la fonction identité x. J’utilise la deuxième ligne du premier tableau.

(24x)’=24(x)’

C’est une fonction de référence , j’utilise la ligne identité du tableau ci-dessous.

(24x)’=24\times 1

(24x)’=24

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}

Voilà ce qu’il faut écrire sur votre copie (dans cette correction, il y a toutes les étapes de calculs pour que chacun de mes abonnés puisse la comprendre)

f'(x)= (2x^3-15x^2+24x)’\\f'(x)= (2x^3)’-(15x^2)’+(24x)’\\f'(x)= 2(x^3)’-15(x^2)’+24(x)’\\f'(x)=2\times3x^2-15\times2x+24\times1\\f'(x)= 6x^2-30x+24

 

Pour montrer que f'(x)=6g(x), on part du membre de gauche, on développe et on arrive au membre de droite. 

6g(x)=6(x^2-5x+4)

\hspace{0.9cm}=6\times x^2-6\times5x+6\times4)

\hspace{0.9cm}=6x^2-30x+24)

\hspace{0.9cm}=f'(x)

On utilise la question précédente pour remplir la ligne du signe de f'(x) qui est du signe de g(x).

On calcule f(1) et f(4) pour compléter la troisième ligne.

f(1)=2\times1^3-15\times1^2+24\times1

\hspace{0.8cm}=2\times1-15\times1+24

\hspace{0.8cm}=2-15+24

\hspace{0.8cm}=11

f(1)=2\times4^3-15\times4^2+24\times4

\hspace{0.8cm}=2\times64-15\times16+96

\hspace{0.8cm}=128-240+96

\hspace{0.8cm}=-16

On peut aussi utiliser la TI-83 Premium CE

On dresse le tableau de variations :

 

 

On détermine l’équation réduite de la tangente à la courbe de f  au point d’abscisse 3.

Je calcule f(3) en remplaçant tous les x par 3 dans f(x)=2x^3-15x^2+24x

f(3)=2\times3^3-15\times3^2+24\times3\\f(3)=2\times27-15\times9+72\\f(3)=54-135+72

f(3)=-9

Pour vérifier avec la TI 83 Premium CE

Je calcule f'(3) en remplaçant tous les x par 3 dans f'(x)=6x^2-30x+24

f'(3)=6\times3^2-30\times3+24\\ f'(3)=6\times9-90+24\\ f'(3)=54-90+24\\ f'(3)=-12

Pour vérifier avec la TI 83 Premium CE

Je remplace a,f(a),f'(a) par 3,(-9),(-12) dans y=f'(a)(x-a)+f(a)

y=-12(x-3)+(-9)

y=-12\times x-12\times(-3)-9

y=-12x+36-9

y=-12x+27

L’équation de la tangente est y=-12x+27.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.