Intégrale d’une fonction continue et positive.
Définition
Le domaine limité par les droites d’équations x=a , x=b , la courbe C_f et l’axe des abscisses est l’ensemble des points M(x;y) vérifiant a\leq x\leq b et 0\leq y\leq f(x).
L’aire de ce domaine est l’intégrale de a à b de la fonction f est notée \int_{a}^{b} f(x) \mathrm{d}x.
Exemple n°1
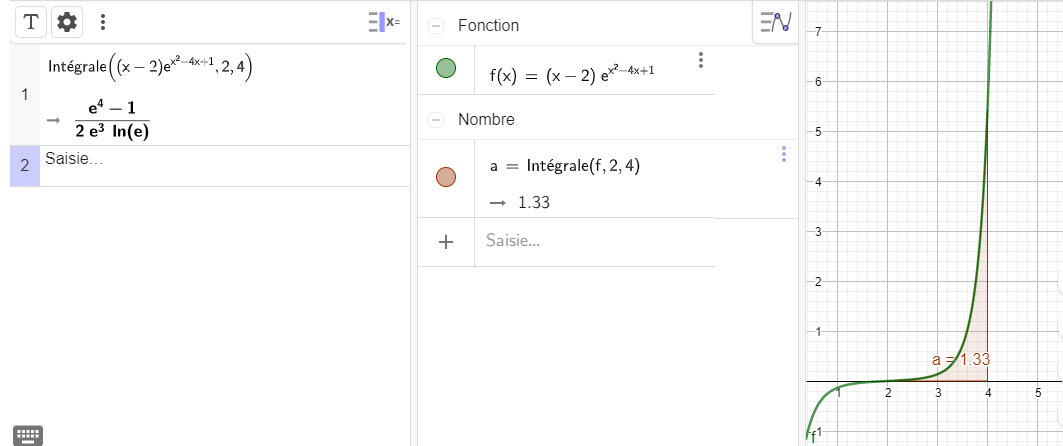
On a choisi dans cet exemple, la fonction carré qui est continue et positive sur \mathbf{R}.
Sur le graphique, on a représenté en bleu \int_{-3}^{-1} x^2 \mathrm{d}x qui vaut 8.67,
en vert \int_{0}^{1} x^2 \mathrm{d}x qui vaut 0.33
et en rouge \int_{0}^{3} x^2 \mathrm{d}x qui vaut 9.
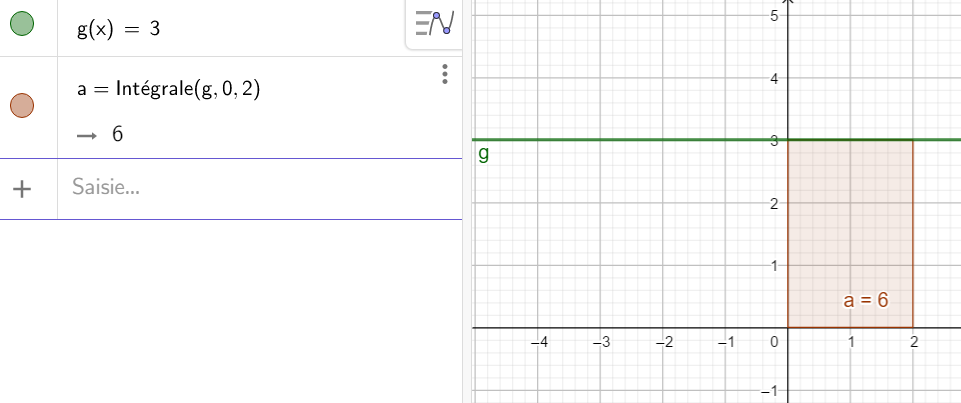
Pour matérialiser l’aire bleue avec Géogébra après avoir saisi la fonction f, il faut dans la colonne de gauche écrire Intégrale(f,-3,-1).
Exercice n°1
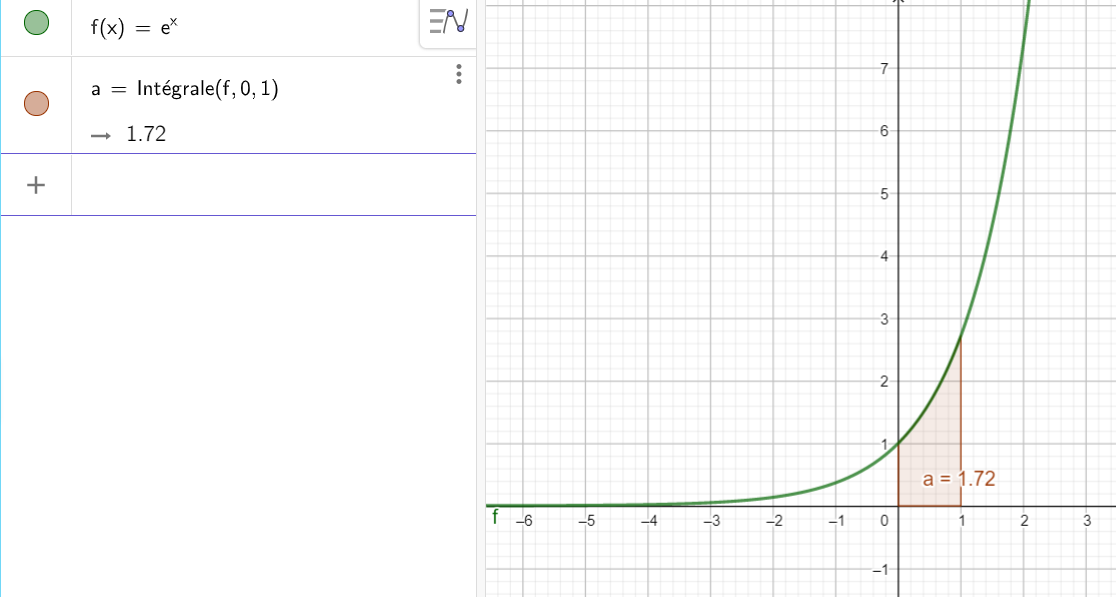
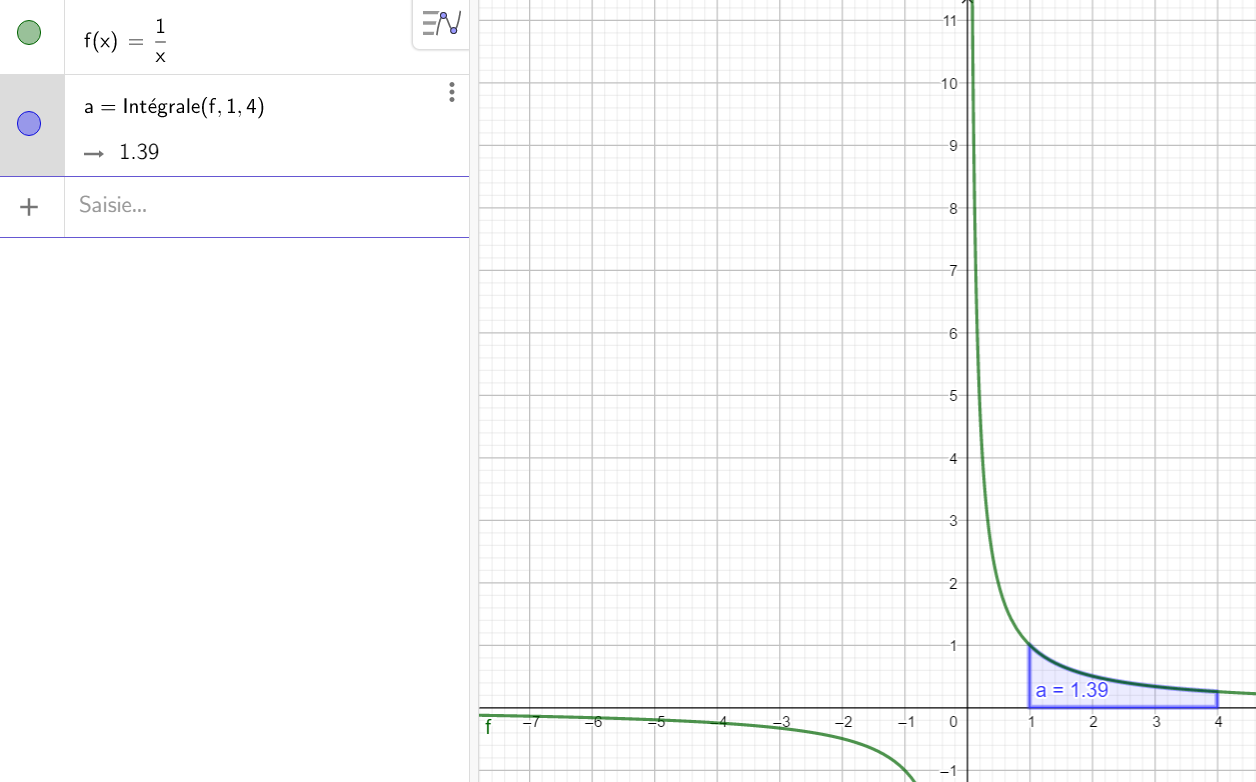
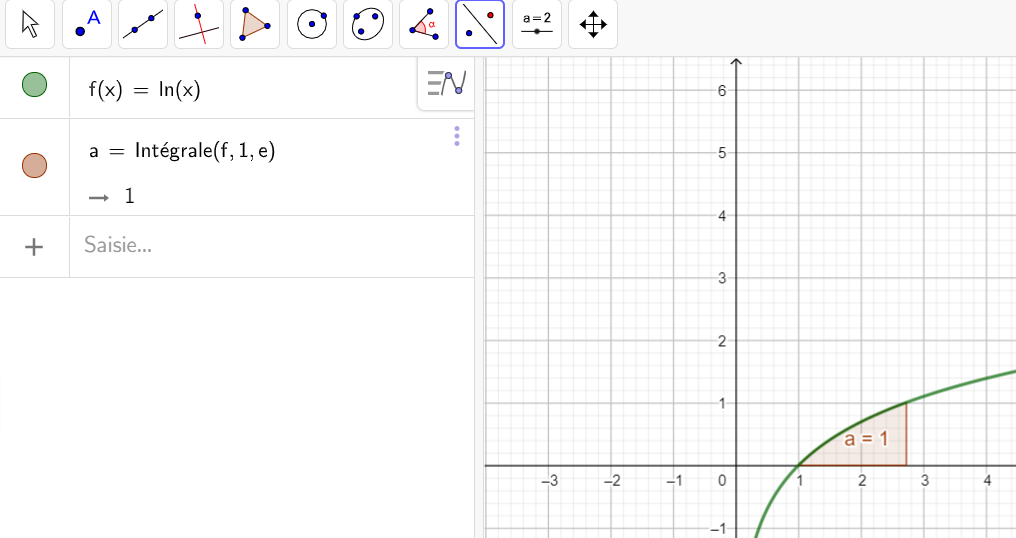
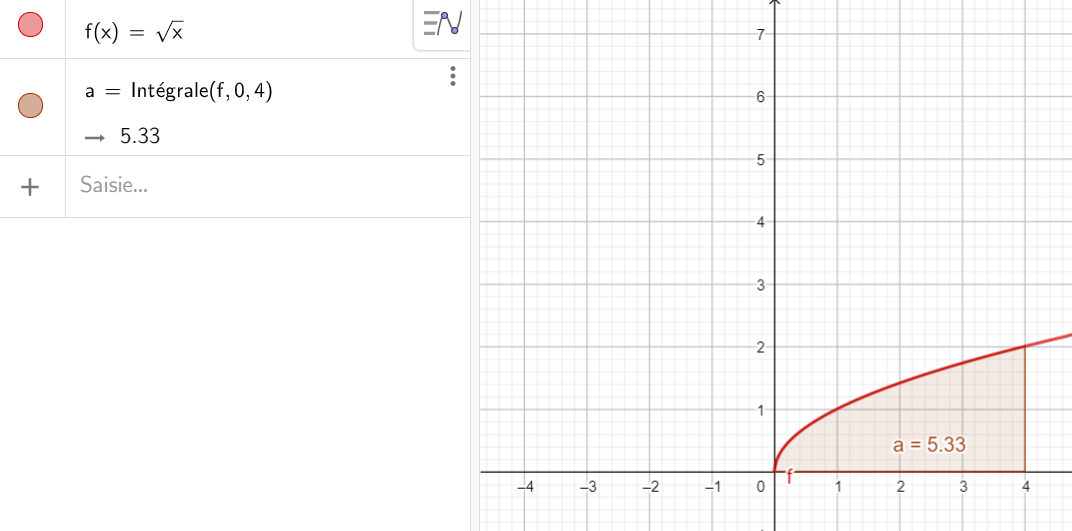
En utilisant la fenêtre Géogébra ci-dessous, évaluer les intégrales suivantes. On choisit pour cet exercice que des fonctions qui seront positives et continues sur l’intervalle qui nous intéresse.
- \int_{0}^{1} e^x \mathrm{d}x
2. \int_{1}^{4} \frac{1}{x} \mathrm{d}x
3. \int_{1}^{e} ln(x) \mathrm{d}x
4. \int_{0}^{4} \sqrt{x} \mathrm{d}x
Exercice n°2
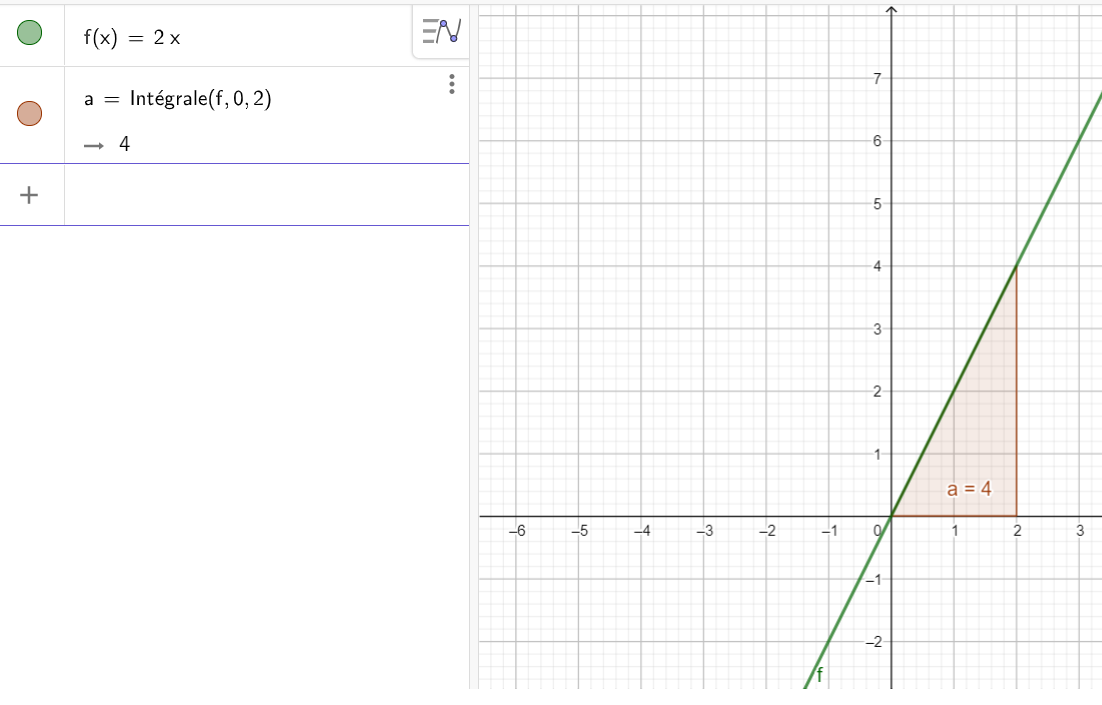
Soit f la fonction définie sur \mathbf{R} par f(x)=2x.
1.En utilisant la fenêtre Géogébra ci-dessus, tracer la courbe de la fonction f .
2.En utilisant la formule suivante pour calculer l’aire d’un triangle \frac{Base\times hauteur}{2}, calculer l’aire du domaine limité par les droites d’équations x=0 , x=2 , l’axe des abscisse et la courbe de f.
Propriété : Relation de Chasles.
Pour tout réel c de [a;b] :
\int_{a}^{c} f(x) \mathrm{d}x+\int_{c}^{b} f(x) \mathrm{d}x=\int_{a}^{b} f(x) \mathrm{d}x
Illustration graphique
On a choisi dans cet exemple, la fonction logarithme népérien qui est continue et positive sur [1;+\infty[.
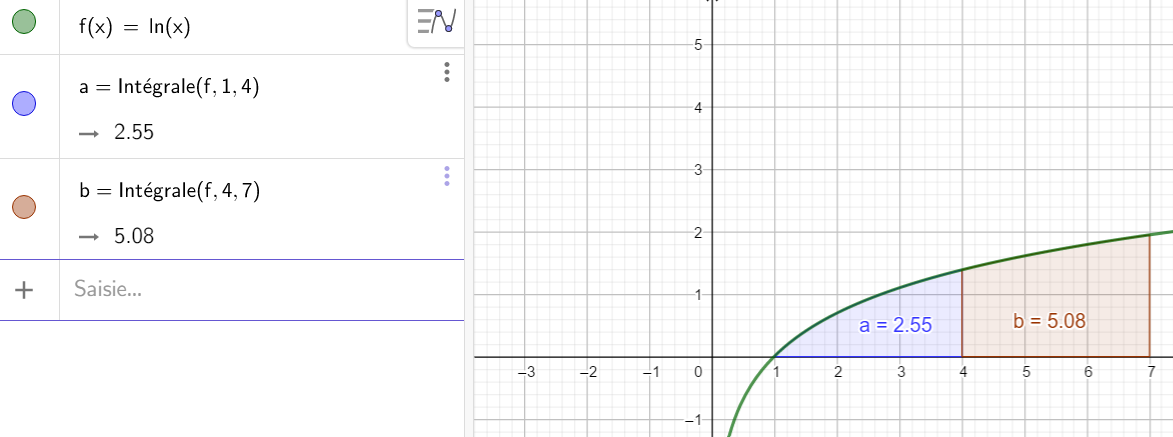
Si on ajoute les aires, on a :
\int_{1}^{4} ln(x) \mathrm{d}x+\int_{4}^{7} ln(x) \mathrm{d}x=2.55+5.08=7.63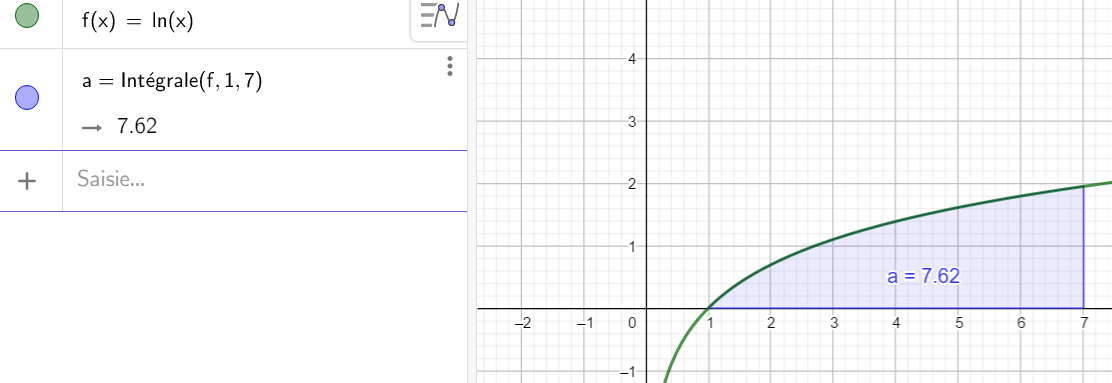
\int_{1}^{7} ln(x) \mathrm{d}x=7.62
Conservation de l’ordre
Si pour tout x de [a;b], on a f(x)\leq g(x) alors \int_{a}^{b} f(x) \mathrm{d}x\leq \int_{a}^{b} g(x) \mathrm{d}x
Illustration graphique
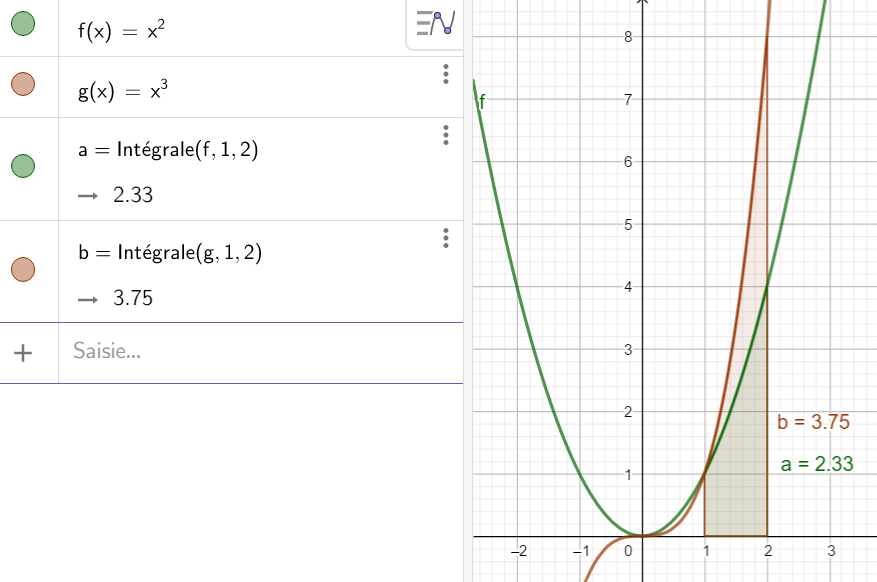
On a choisi dans cet exemple, les fonctions carré et cube qui sont continues et positives sur [1;2].
On voit bien que sur [1;2] on a x^2\leq x^3 ( la courbe verte est située sous la courbe rouge) et que l’on a
\int_{1}^{2} x^2 \mathrm{d}x\leq \int_{1}^{2} x^3 \mathrm{d}x (2.33\leq 3.75).
Valeur moyenne
La valeur moyenne de f sur l’intervalle [a;b] est le réel \frac{1}{b-a}\int_{a}^{b} f(x) \mathrm{d}x
Illustration graphique
On a choisi dans cet exemple une fonction continue et positive sur [-2;2].
L’aire limitée par la courbe, l’axe des abscisse, les droites d’équations : x=-2 et x=2 mesure 8.

Si on calcule (-2)-2 on obtient 4 qui est la distance sur l’axe des abscisses entre -2 et 2. Nous dirons que c’est la longueur d’un rectangle. L’aire trouvée précédemment est 8. Pour trouver la largeur ( on dit aussi la hauteur ) on va diviser 8 par 4 ce qui donne 2.
On s’intéresse à la fonction constante g(x)=2
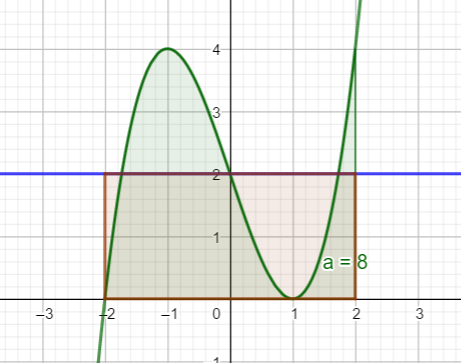
\int_{-2}^{2} g(x) \mathrm{d}x est aussi égale à 8. Ainsi si on remplaçait tous les f(x) par la valeur 2, on obtiendrait toujours une aire égale à 8
La valeur moyenne de la fonction f sur l’intervalle [-2;2] est donc 2.
Exercice n°3
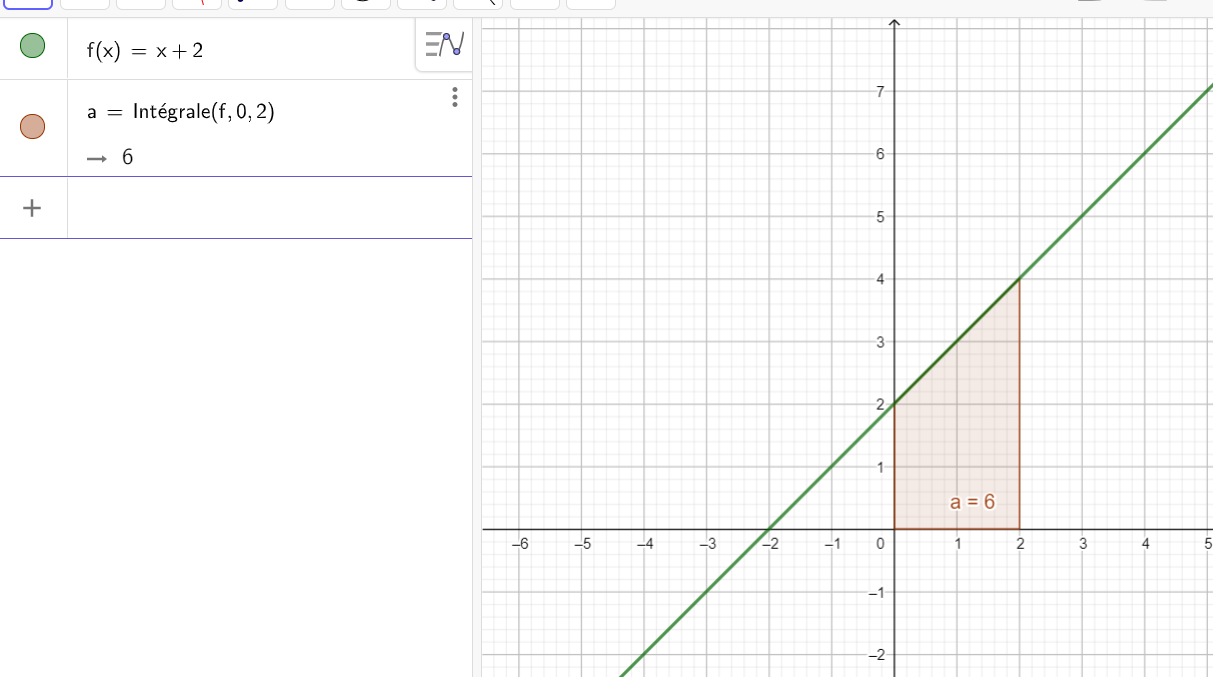
Soit f la fonction définie sur \mathbf{R} par f(x)=x+2.
1.En utilisant la fenêtre Géogébra ci-dessus, tracer la courbe de la fonction f .
2.En utilisant la formule suivante pour calculer l’aire d’un trapèze \frac{(petite\hspace{0.1cm} base+grande\hspace{0.1cm} base)\times hauteur}{2}, calculer l’aire du domaine limité par les droites d’équations x=0 , x=2 , l’axe des abscisse et la courbe de f.
3. En déduire la valeur moyenne de f sur l’intervalle [0;2].
Inégalité de la moyenne
Si pour tout x de [a;b], il existe m et Mtels que m\leq x\leq M alors m(b-a)\leq\int_{a}^{b} f(x) \mathrm{d}x\leq M(b-a)
Exercice n°4
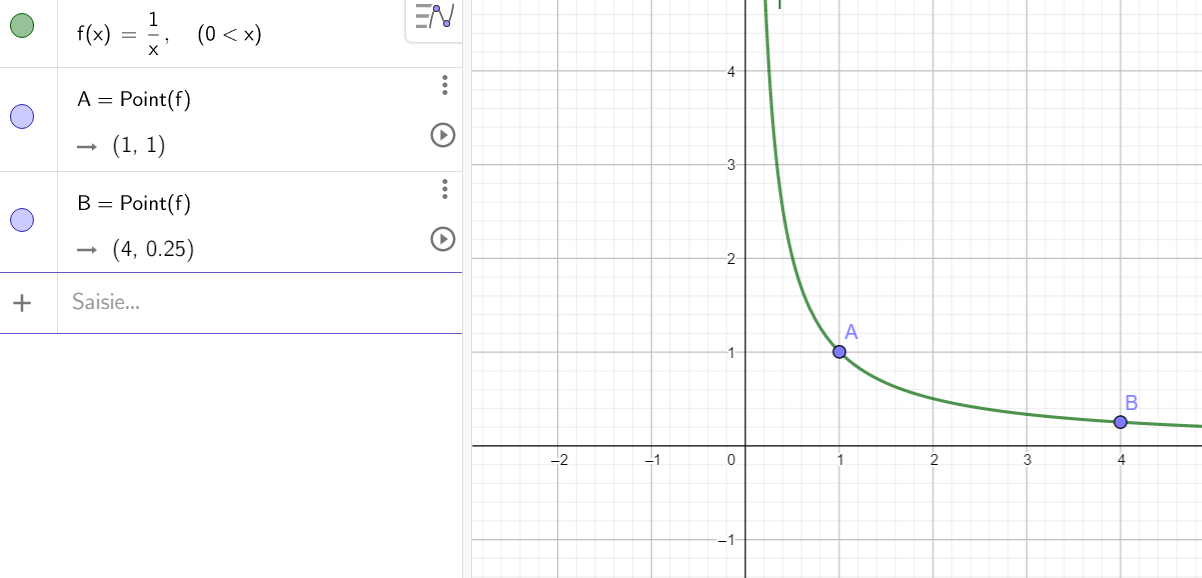
Soit f la fonction inverse définie sur ]0;+\infty[ par f(x)=\frac{1}{x}.
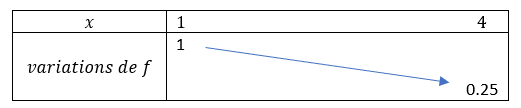
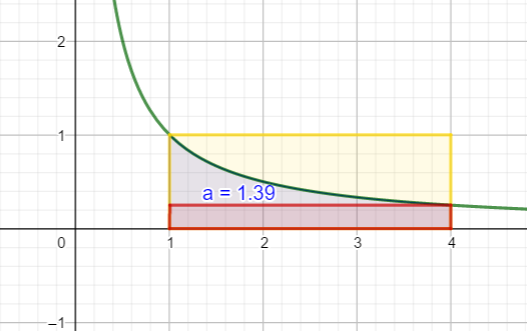
1.En utilisant la fenêtre Géogébra ci-dessus, tracer la courbe de la fonction f . A l’aide du graphique, dresser son tableau de variations sur l’intervalle [1;4] et en déduire un encadrement de f(x) sur [1;4].
2.Déduire de la question n°1, un encadrement de \int_{1}^{4} f(x) \mathrm{d}x.
Cas général
Théorème fondamental
Si f est une fonction continue et positive sur un intervalle [a;b], alors la fonction F définie sur [a;b] par F(x)=\int_{a}^{x} f(t) \mathrm{d}t est dérivable sur [a;b] et a pour dérivée f.
Définition (la fonction est de signe quelconque)
Soit f une fonction continue sur un intervalle [a;b] et F une primitive de f sur [a;b], alors
\int_{a}^{b} f(x) \mathrm{d}x=F(b)-F(a).
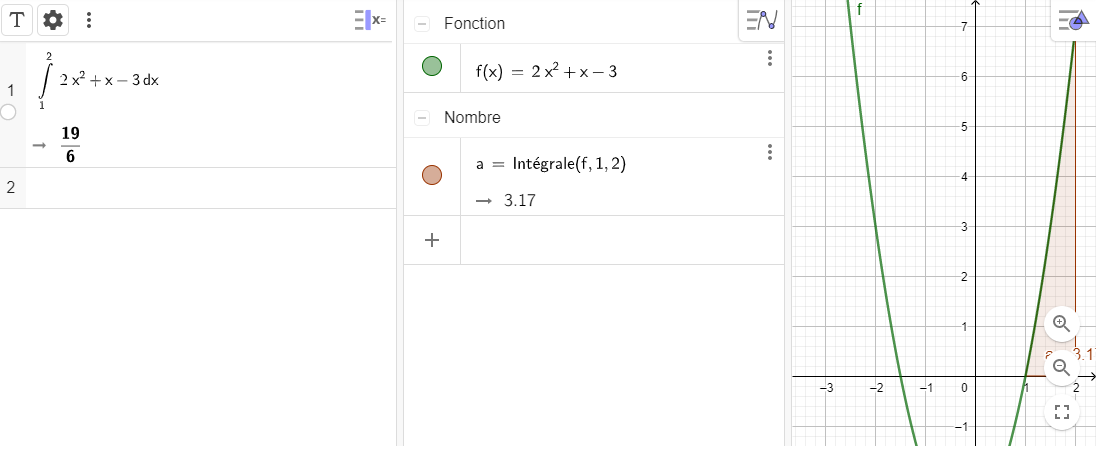
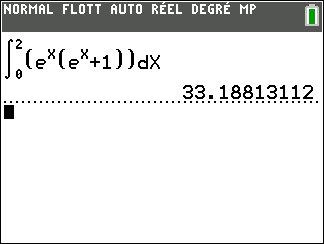
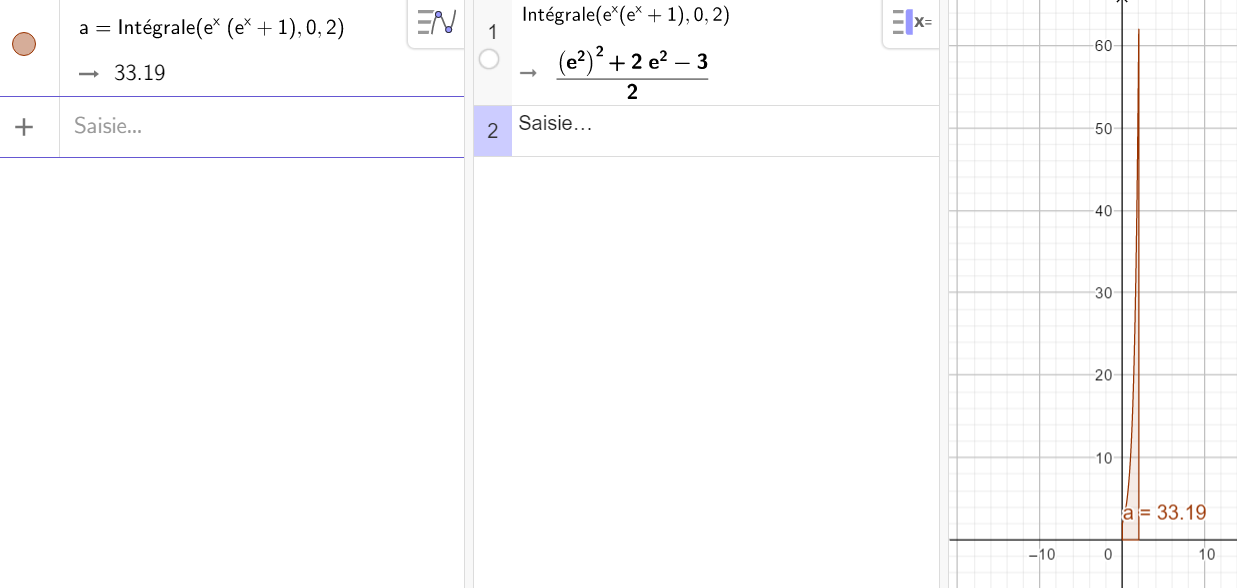
Exercice n°5
Calculer les intégrales suivantes.
Avant de se lancer dans le calcul, conjecturer avec cette page Géogébra. L’exemple proposé correspond à la question n°1. Pour les autres questions, changer juste la fonction et les bornes.
6. \int_{1}^{4} \frac{1}{\sqrt{x}} \mathrm{d}x
Exercice n°6
Après avoir vérifié dans chaque cas que la fonction F est une primitive de la fonction f, calculer les intégrales suivantes.
- \int_{-1}^{0} (3x+1)e^{3x} \mathrm{d}x
avec F(x)=xe^{3x}
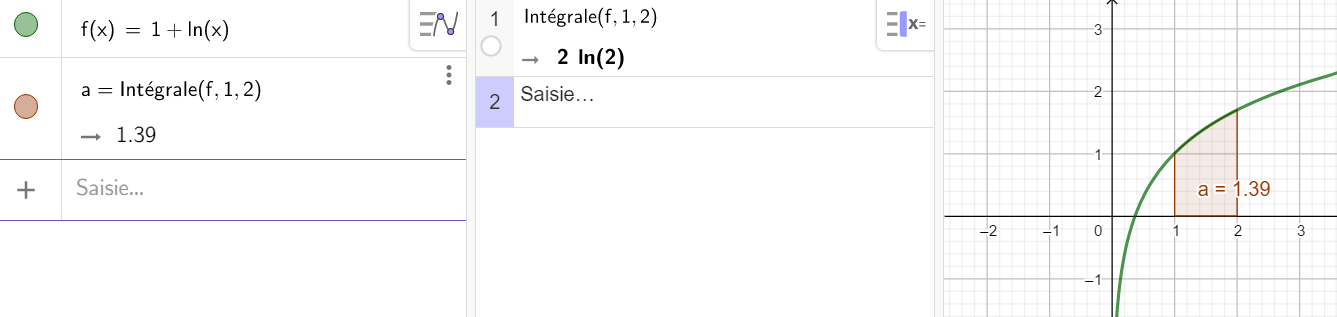
2. \int_{1}^{2} 1+ln(x) \mathrm{d}x
avec F(x)=1+ln(x)
3. \int_{1}^{e} x-1-ln(x) \mathrm{d}x
avec F(x)=0.5x^2-xln(x)
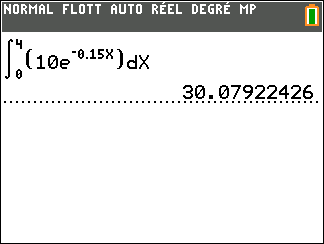
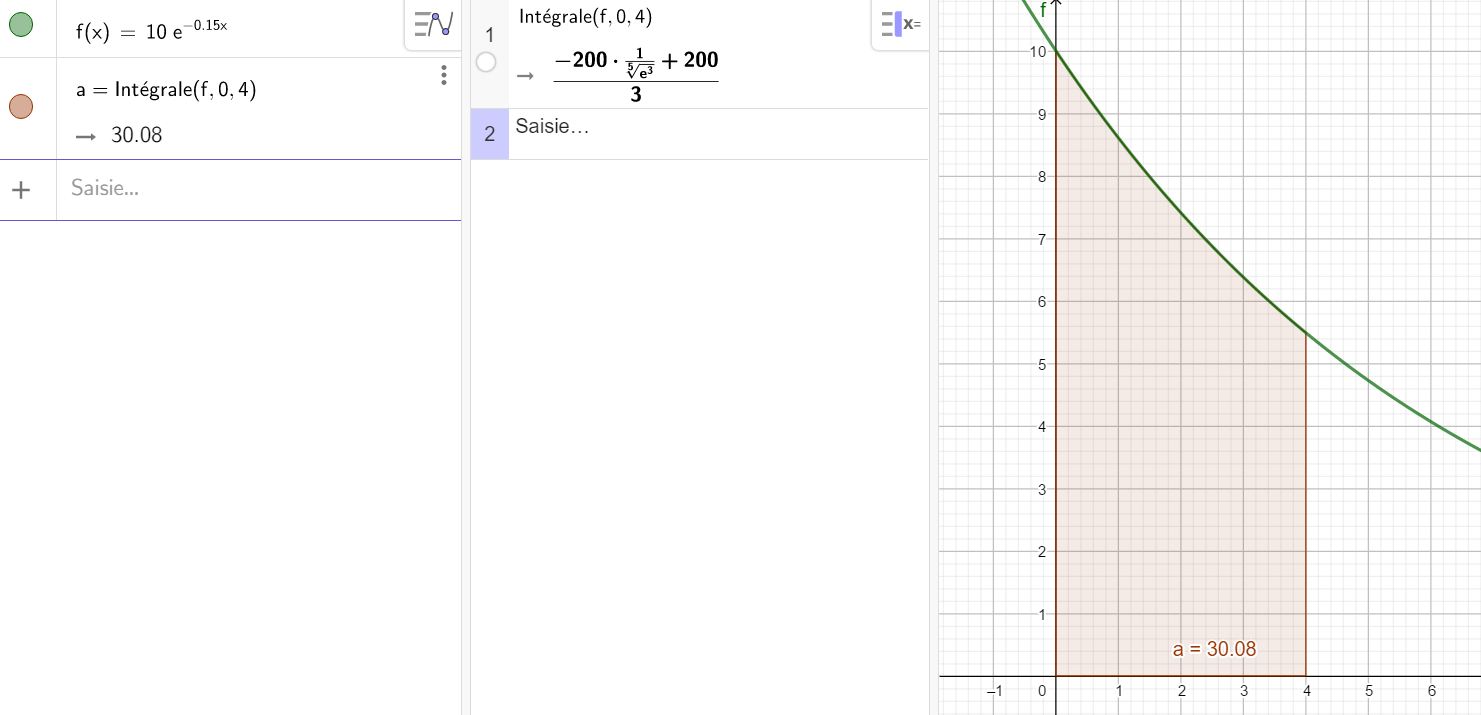
4. \int_{0}^{4} 10e^{-0.15t} \mathrm{d}x
avec F(x)=-\frac{200}{3}e^{-0.15t}
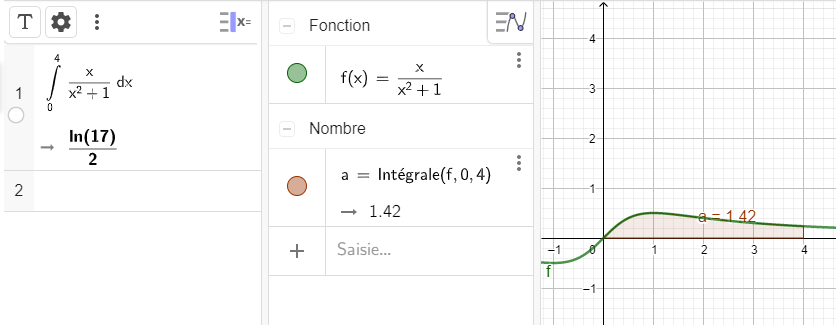
Exercice n°7
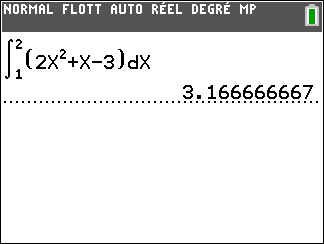
Calculer les intégrales suivantes.
Avant de se lancer dans le calcul, conjecturer avec cette page Géogébra. L’exemple proposé correspond à la question n°1. Pour les autres questions, changer juste la fonction et les bornes.
Définition (linéarité de l’intégrale)
Quelques soient f et g deux fonctions continues sur un intervalle [a;b] et pour tous réels \Alpha et \Beta\\\int_{a}^{b} (\alpha f(x)+\beta g(x)) \mathrm{d}x=\alpha \int_{a}^{b} f(x) \mathrm{d}x+\beta \int_{a}^{b} g(x) \mathrm{d}x.