Exercice n°1
On lance deux fois de suite une pièce équilibrée.
Si le joueur obtient 2 Faces, il perd 12 euros, s’il obtient exactement une Face, il gagne 2 euros, s’il
obtient 2 Piles il gagne 8 euros. On note X la variable aléatoire correspondant au gain algébrique
du joueur.
a) E(X)=0 | b) E(X)=-2 | c) E(X)=-\frac{2}{3} | d) E(X)=1 |
Exercice n°2
A et B sont deux évènements tels que p(A)=\frac{2}{5} , p(B)=\frac{1}{2} et p(A\cup B)=\frac{4}{5}
a) A et B sont incompatibles | b) p(A\cap B)=\frac{1}{10} | c) p_A(B)=\frac{1}{2} | d) p_B(A)=\frac{5}{8} |
Exercice n°3
On donne l’arbre de probabilités ci-contre, ainsi que la probabilité p(C)=0.26.
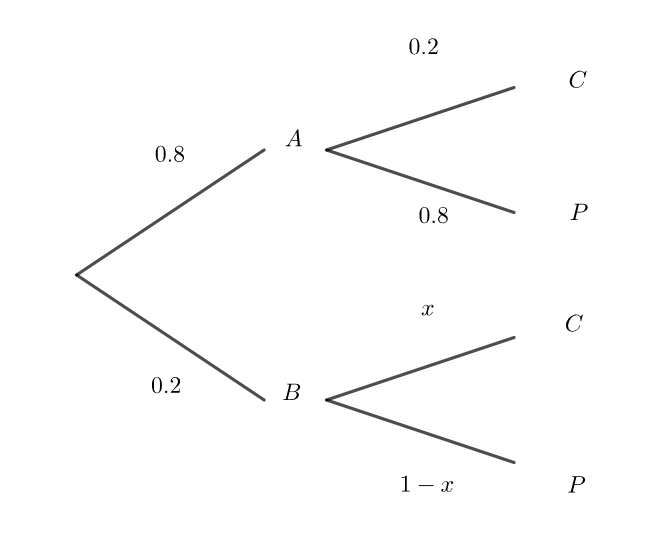
a) x=0.13 | b) x=0.06 | c) x=0.26 | d) x=0.5 |
Exercice n°4
Dans une usine 4\% des téléphones produits sont défectueux. On constate qu’au cours du contrôle qualité, si le téléphone est bon, il est accepté dans 98\% des cas, et que si il est défectueux il est refusé dans 96\% des cas.
La probabilité qu’un téléphone soit refusé est égale à :
a) 0.04 | b) 0.98 | c) 0.0576 | d) p_B(A)=0.9224 |
Exercice n°5
On donne l’arbre de probabilités ci-contre, sur lesquel des données ont été malheureusement effacées.
Quelle affirmation est exacte ?
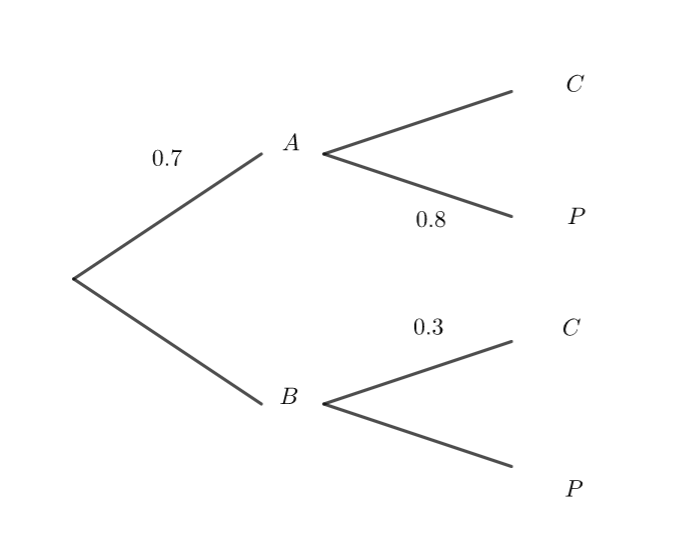
a) p(A\cap P)=1.5 | b) p(C)=0.5 | c) p(C)=0.23 | d) p_C(B)=0.3 |
Exercice n°6
On note X la variable aléatoire qui représente le gain algébrique en euros d’un joueur. La loi de probabilité de X est donnée par le tableau suivant :
| a | -2 | 0 | 8 |
| p(X=a) | 0.5 | 0.2 | 0.3 |
Le gain moyen espéré par le joueur est :
a) 0.33 | b) 2 | c) 0.5 | d) 1.4 |
Exercice n°7
A et B sont deux évènements indépendants tels que p(A)=0.25 et P(B)=0.4.
Alors p(A\cup B)est égal à :
a) 0.65 | b) On ne peut pas savoir | c) 0.1 | d) 0.325 |
Exercice n°8
En utilisant l’arbre de probabilités ci-contre.
On obtient p(C)=
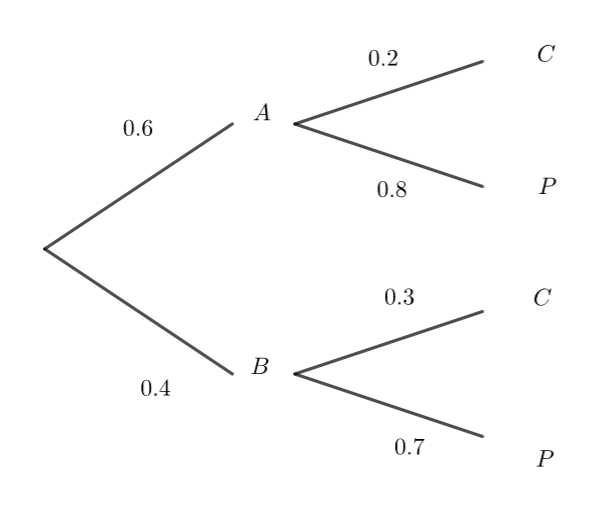
a) 0.5 | b) 0.2 | c) 0.3 | d) 0.24 |



