Exercice n°1
La droite D est la tangente à la courbe C_f au point d’abscisse A(-2;0)
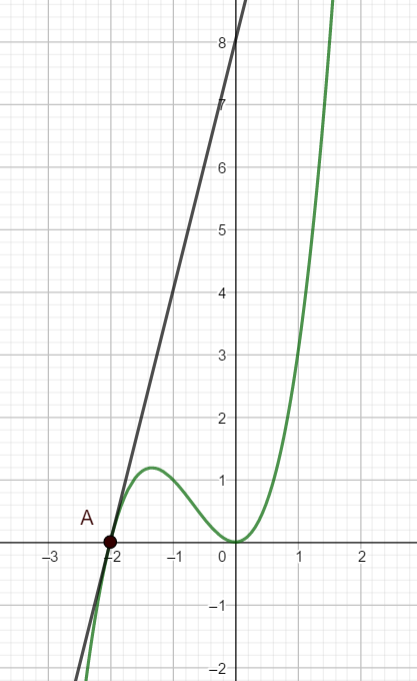
f'(-2) est égal à :
a) 0 | b) 8 | c) 4 | d) \frac{1}{4} |
Exercice n°2
Soit f la fonction définie sur \mathbf{R} par f(x)=x^2-4x+1. Une équation de la tangente à la courbe représentative de f dans un repère orthonormé au point d’abscisse -1 est :
a) y=-6x+12 | b) y=-5x+1 | c) y=-6x | d) y=-6 |
Exercice n°3
La fonction f définie sur \mathbf{R} par f(x)=(-2x+4)^3 a pour fonction dérivée:
a) f'(x)=(-2)^3 | b) f'(x)=3(-2x+4)^2 | c) f'(x)=6(-2x+4)^2 | d) f'(x)=-6(-2x+4)^2 |
Exercice n°4
La fonction f définie sur [0;+\infty[ par f(x)=\frac{x^2-2}{2x+1}.
a) La courbe de f n’a pas de tangente en 0 | b) La courbe de f admet une tangente parallèle à l’axe des abscisses en 0 | c) La courbe de f admet une tangente qui a pour équation réduite y=4x-2 | d) La courbe de f admet une tangente qui a comme coefficient directeur -4 en 0 |
Exercice n°5
La fonction f définie sur [0;+\infty[ par f(x)=\frac{2x-2}{x+1} a pour fonction dérivée:
a) f'(x)=2 | b) f'(x)=\frac{4x}{(x+1)^2} | c) f'(x)=-\frac{4}{(x+1)^2} | d) f'(x)=\frac{4}{(x+1)^2} |
Exercice n°6
La fonction f définie sur [0;+\infty[ par f(x)=\frac{x^2}{x+1}.
Le coefficient directeur de la tangente à la courbe de f au point d’abscisse 1 est égal à
a) 2 | b) \frac{3}{4} | c) \frac{5}{4} | d) \frac{3}{2} |
Exercice n°7
La droite D est la tangente à la courbe C_f au point d’abscisse A(2;-2.5)
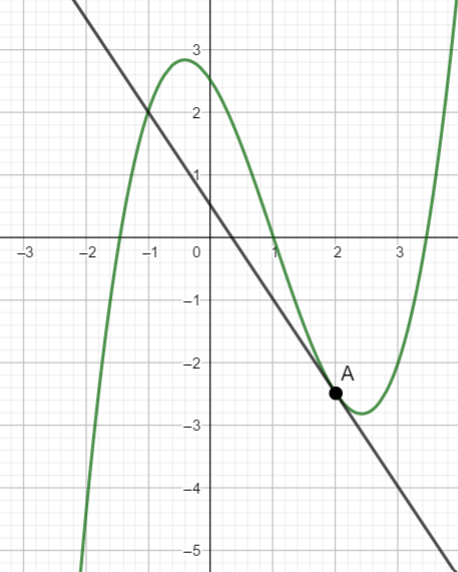
L’équation de la tangente D est égale à :
a) y=\frac{3}{2}(x-2)-\frac{5}{2} | b) y=-\frac{5}{2}(x-2)-\frac{3}{2} | c) y=-\frac{3}{2}(x+2)-\frac{5}{2} | d) y=-\frac{3}{2}(x-2)-\frac{5}{2} |
Exercice n°8
La fonction f définie sur ]0;+\infty[ par f(x)=x^2+\frac{1}{x}.
Le coefficient directeur de la tangente à la courbe de f au point d’abscisse 1 est égal à
a) 3 | b) 1 | c) 0 | d) 2 |



