Exercice n°1 ( tester si un nombre est racine évidente d’un polynôme du second degré )
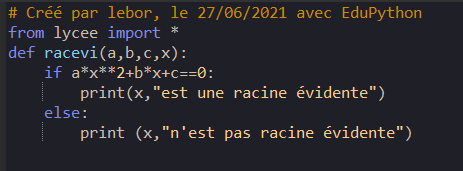
1. On se propose d’écrire un programme en Python qui teste si oui ou non un nombre x est racine évidente de l’équation ax^2+bx+c=0.
Il débutera par l’instruction :
def racevi(a,b,c,x)
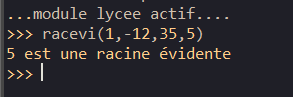
2. Que renvoie le programme si on entre 1,-12,35,5 pour a,b,c,x. Que peut-on en conclure ?
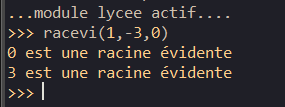
Exercice n°2 ( rechercher une racine évidente d’un polynôme du second degré )
Remarque : en général lorsqu’on parle de racine évidente, on pense aux nombres entiers de -3 à 3.
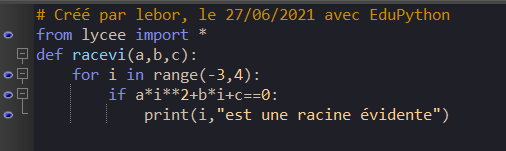
1. On se propose d’écrire un programme en Python qui recherche les racines évidentes de l’équation ax^2+bx+c=0 parmi les nombres entiers de -3 à 3 .
Il débutera par l’instruction :
def racevi(a,b,c)
2. Que renvoie le programme si on entre 1,-3,0 pour a,b,c. Que peut-on en conclure ?
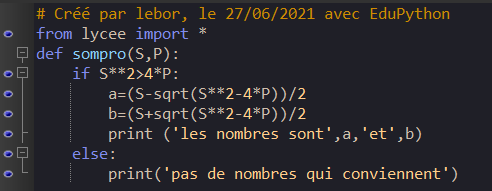
Exercice n°3 ( déterminer deux nombres dont on connaît la somme notée S et le produit noté P )
Remarque : il faut que S^2>4P.
1. On se propose d’écrire un programme en Python qui détermine les nombres dont on connaît la somme et le produit.
Il débutera par l’instruction :
def sompro(S,P)
2. Que renvoie le programme si on entre 1,-6 pour S,P ?
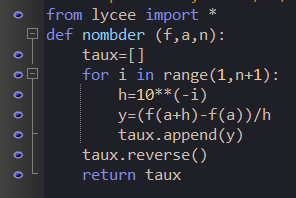
Exercice n°4 ( taux d’accroissement et nombre dérivé)
1. Compléter les pointillés pour que le programme Edupython suivant retourne la liste des valeurs des taux d’accoissement qui se rapprochent du nombre dérivé en a.

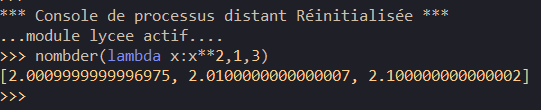
2. Que renvoie le programme si on entre nombder(lamba x: x**2,1,3) ?
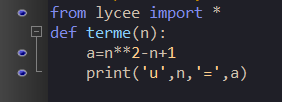
Exercice n°5 ( calculer le terme d’une suite définie par formule explicite )
1. On se propose d’écrire un programme en Python qui calcule le terme u_n de la suite (u_n) définie de façon explicite par u_n=n**2-4n+2. Compléter les pointillés.
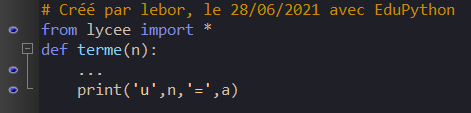
2. Que renvoie le programme si on entre terme(7) dans la console ?
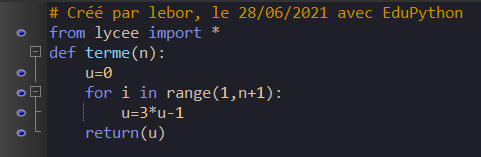
Exercice n°6 (calculer le terme d’une suite définie par récurrence)
1. On se propose d’écrire un programme en Python qui calcule le terme u_n de la suite (u_n) définie par récurrence par u_0=0 et u_{n+1}=3u_n-1. Compléter les pointillés.
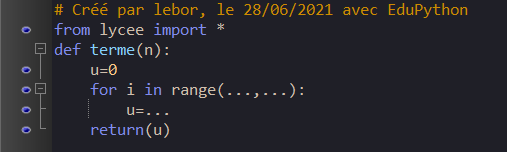
2. Que renvoie le programme si on entre terme(7) dans la console ?
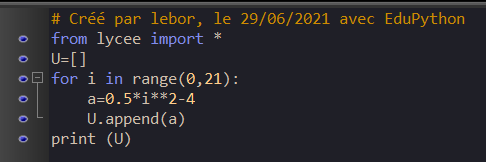
Exercice n°7 ( calculer les premiers termes d’une suite définie par formule explicite )
On se propose d’écrire un programme en Python qui affiche les 21 premiers termes de la suite (u_n) définie de façon explicite par u_n=0.5n^2-4.
On utilisera une liste.
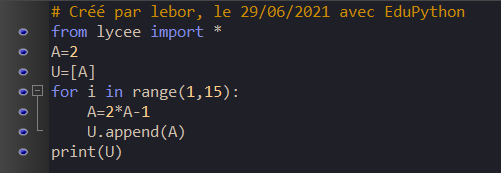
Exercice n°8 (calculer les premiers termes d’une suite définie par récurrence)
On se propose d’écrire un programme en Python qui affiche les 15 premiers termes de la suite (u_n) définie par u_0=2 u_{n+1}=2u_n-1.
On utilisera une liste.