Soit f la fonction définie sur \mathbf{R} par f(x)=x^2-4x+1. Une équation de la tangente à la courbe représentative de f dans un repère orthonormé au point d’abscisse -1 est :
a) y=-6x+12 | b) y=-5x+1 | c) y=-6x | d) y=-6 |
Tout ce qui est proposé est réalisable même si la calculatrice est en mode examen.
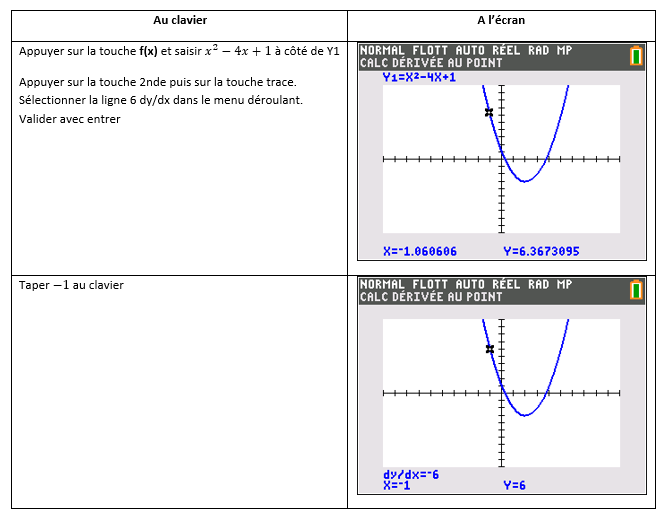
On remplace a par (-1), f(a) par 6 et f'(a) par (-6) dans l’équation de la tangente
y=f'(a)(x-a)+f(a).
y=(-6)(x-(-1))+6\\y=-6x-6+6\\y=-6xLa bonne réponse est : c) y=-6x.
Réponse:
\overrightarrow{DC}=\overrightarrow{HG}.
Résoudre graphiquement f(x)=1
C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.
Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.
Les antécédents sont -2 et 2.
Donc S=\{-2;2\}
Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.
