Exercice de synthèse sur les fonctions en seconde

Déterminer par le calcul, à l’aide d’une expression algébrique du type f(x)=?, des images et des antécédents, Développer une expression littérale, Equations réduites de droites, Factoriser une expression littérale, Fonctions, Niveau seconde, Nombres et calculs, Résoudre une équation du second degré en classe de seconde, Résoudre une inéquation du second degré en classe de seconde à l’aide d’un tableau de signes, Variations d’une fonction

Partie 1

Soit la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=(2x-1)^{2}-4$ .

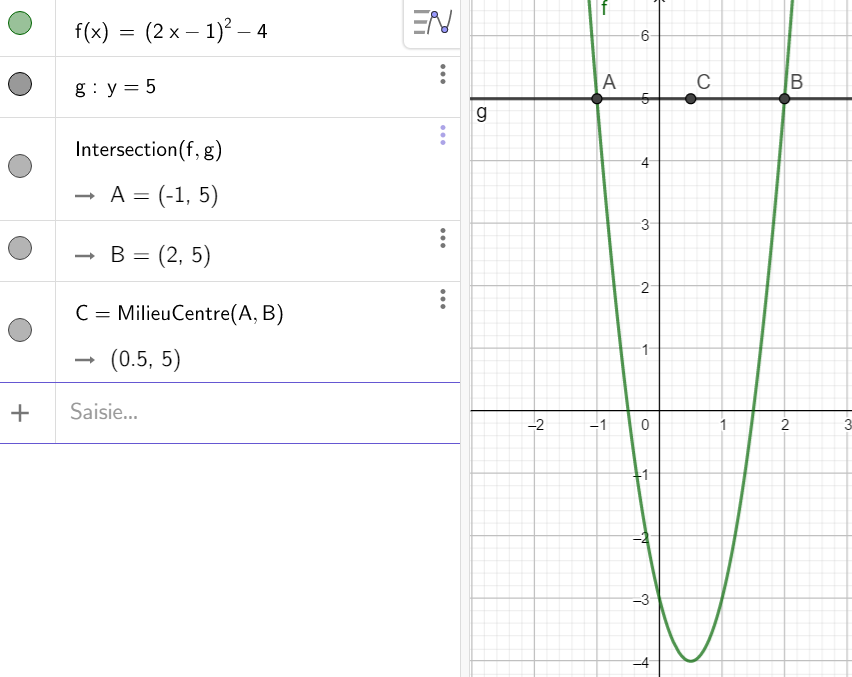
Nous allons utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider nos réponses . Il y a trois colonnes : Algèbre, Calcul Formel et Graphique.

Déterminer la forme développée et réduite de $f(x)$ .

Pour conjecturer le résultat, taper $(2x-1)^{2}-4$ sur la ligne n°1 de la colonne Calcul formel et appuyer sur le cinquième onglet.

2. Déterminer la forme factorisée de $f(x)$ .

Pour conjecturer le résultat, taper $(2x-1)^{2}-4$ sur la ligne n°2 de la colonne Calcul formel et appuyer sur le quatrième onglet.

3. En utilisant l’une des trois formes suivantes

(e) $f(x)=(2x-1)^{2}-4$

(d) $f(x)=4x^{2}-4x-3$

(f) $f(x)=(2x-3)(2x+1)$

Déterminer les images de $\frac{1}{2}$ , $\sqrt{2}$ , $0$ et $\frac{3}{2}$ .

On conjecture les réponses avec la TI 83 Premium CE.

4. En utilisant l’une des trois formes suivantes

(e) $f(x)=(2x-1)^{2}-4$

(d) $f(x)=4x^{2}-4x-3$

(f) $f(x)=(2x-3)(2x+1)$

Déterminer le(s) éventuel(s) antécédent(s) de $-4$ , $-3$ , $0$ et $12$ .

Avec Géogébra :On conjecture les antécédents en utilisant la colonne Calcul Formel de la fenêtre Géogébra située au début de l’exercice. Pour déterminer le(s) éventuel(s) antécédent(s) de $-4$ , taper f(x)=-4 sur la ligne n°3 et cliquer sur le septième onglet ( $X=$ ).

Avec la TI 83 Premium :On conjecture les antécédents ainsi

Remarque avant de commencer utiliser la forme développée et faire apparaître 0 à droite.

Par exemple pour résoudre $f(x)=12$ , écrire $4x^2-4x-3=12$ puis $4x^2-4x-15=0$

5. En utilisant l’une des trois formes suivantes

(e) $f(x)=(2x-1)^{2}-4$

(d) $f(x)=4x^{2}-4x-3$

(f) $f(x)=(2x-3)(2x+1)$

Résoudre $f(x)\leq 0$ , $f(x)>-3$ et $f(x)<1$ .

On conjecture l’ensemble solution en utilisant la colonne Calcul Formel de la fenêtre Géogébra située au début de l’exercice. Pour résoudre $f(x)\leq 0$ , taper $f(x)\leq 0$ sur la ligne n°3 et cliquer sur le septième onglet ( $X=$ ).

Partie 2

Soient les deux points $A(-1;5)$ et $B(1;-3)$ .

Déterminer l’équation réduite de la droite $d$ qui passe par $A$ et $B$ c’est possible.

On conjecture l’équation réduite de la droite $(AB)$ avec la fenêtre Géogébra située au début de l’exercice. On place $A$ et $B$ en tapant $A=(-1,5)$ et $B=(1,-3)$ dans la colonne Algèbre. Puis on clique sur le troisième onglet et on sélectionne droite dans le menu déroulant. dans le repère on clique sur le point $A$ et sur le point $B$ . Une équation de $(AB)$ apparaît dans la colonne Algèbre. Pour avoir l’équation réduite, cliquer droit sur l’équation et sélectionner Equation $y=ax+b$ dans le menu déroulant.

2. Déterminer pour quelles valeurs de $x$ la courbe de la fonction $f$ est située strictement sous la droite $d$ .

On utilisera la forme développée de $f(x)$ .

On conjecture l’ensemble solution en utilisant la colonne Calcul Formel de la fenêtre Géogébra située au début de l’exercice. Pour résoudre $f(x)< -4x+1$ , taper $f(x)< -4x+1$ sur la ligne n°3 et cliquer sur le septième onglet ( $X=$ ).

Partie 3

a. Résoudre $f(x)=5$

1.b. En déduire l’abscisse du sommet de la parabole.

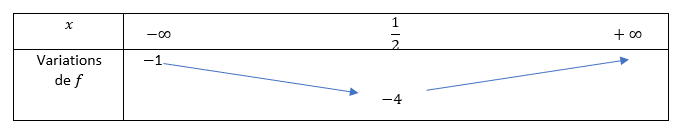
2. En déduire le tableau de variations de $f$ sur $\mathbf{R}$ .

Pour résoudre $f(x)<1$ on va utiliser e) $(2x-1)^{2}-4$

L’inéquation à résoudre $(2x-1)^{2}-4<1$ est du 2nd degré car en développant $(2x-1)^{2}$ le plus grand exposant de $x$ est 2.

La méthode proposée concerne les inéquations du second degré.

$(2x-1)^{2}-4 <1$

1.Je fais tout passer à gauche, zéro apparaît à droite.

le $1$ à droite du signe égal n’est pas à sa place, j’enlève $1$ de chaque côté.

$(2x-1)^{2}-4-1 <0$

$(2x-1)^{2}-5 <0$

2. Je factorise le membre de gauche.

a. Il n’y a pas de facteur commun.

b. J’utilise l’identité remarquable $a^{2}-b^{2}=(a-b)(a+b)$ pour factoriser $(2x-1)^{2}-5$

$a^{2}=(2x-5)^{2} \hspace{2cm}a=(2x-5)$

$b^{2}=5\hspace{3.2cm}b=\sqrt{5}$

Je remplace $a$ et $b$ par $(2x-1)$ et $\sqrt{5}$ dans $a^{2}-b^{2}=(a-b)(a+b)$

$(2x-1-\sqrt{5})(2x-1+\sqrt{5}) >0$

3. J’écris la phrase d’introduction.

Je cherche pour quelles valeurs de $x$ , le produit $(2x-1-\sqrt{5})(2x-1+\sqrt{5})$ est de signe $(-)$ .

4. Je prépare mon tableau de signes.

Je résous $2x-1-\sqrt{5}=0\\2x=1+\sqrt{5}\\x=\frac{1+\sqrt{5}}{2}$

Je résous $2x-1+\sqrt{5}=0\\2x=1-\sqrt{5}\\x=\frac{1-\sqrt{5}}{2}$

Je place les valeurs $\frac{1+\sqrt{5}}{2}$ et $\frac{1-\sqrt{5}}{2}$ sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.

Je remplis le tableau avec des signes $(-)$ , $(+)$ , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur $2x-1-\sqrt{5}$ , comme $a=2$ , on commence par le signe $(-)$ jusqu’au zéro et on complète avec des $(+)$ .

Sur la ligne du facteur $2x-1+\sqrt{5}$ , comme $a=2$ , on commence par le signe $(-)$ jusqu’au zéro et on complète avec des $(+)$ .

Pour compléter la ligne du produit $(2x-1-\sqrt{5})(2x-1+\sqrt{5})$ , j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit $(2x-1-\sqrt{5})(2x-1+\sqrt{5})$ est de signe $(-)$ pour la deuxième colonne qui correspond aux valeurs de x comprises entre $\frac{1-\sqrt{5}}{2}$ et $\frac{1+\sqrt{5}}{2}$ .

Je ne prends pas les valeurs $\frac{1-\sqrt{5}}{2}$ et $\frac{1+\sqrt{5}}{2}$ car le produit ne peut pas être nul. Donc j’ouvre les crochets en $\frac{1-\sqrt{5}}{2}$ et $\frac{1+\sqrt{5}}{2}$ , ce qui signifie que les crochets sont tournés vers l’extérieur.

S=]\frac{1-\sqrt{5}}{2};\frac{1-\sqrt{5}}{2}[

Pour résoudre $f(x)<-4x+1$ on va utiliser d) $4x^2-4x-3$

L’inéquation à résoudre $4x^2-4x-3<-4x+1$ est du 2nd degré.

La méthode proposée concerne les inéquations du second degré.

4x^2-4x-3<-4x+1

1.Je fais tout passer à gauche, zéro apparaît à droite.

le $-4x+1$ à droite du signe égal n’est pas à sa place, j’ajoute $4x-1$ de chaque côté.

4x^2-4x-3+4x-1<0\\4x^2-4<0

2. Je factorise le membre de gauche.

a. Il y a un facteur commun.

$4x^2=4\times x^2$

$4=4\times 1$

4(x^2-1)<0

b. J’utilise l’identité remarquable $a^{2}-b^{2}=(a-b)(a+b)$ pour factoriser $x^2-1$

$a^{2}=x^2 \hspace{2cm}a=x$

$b^{2}=1\hspace{2.2cm}b=1$

Je remplace $a$ et $b$ par $x$ et $1$ dans $a^{2}-b^{2}=(a-b)(a+b)$

$4(x-1)(x+1) <0$

3. J’écris la phrase d’introduction.

Au lieu d’écrire je cherche pour quelles valeurs de $x$ , le produit $4(x-1)(x+1)$ est de signe $(-)$ .

Comme 4 est positif, on peut écrire :

Je cherche pour quelles valeurs de $x$ , le produit $(x-1)(x+1)$ est de signe $(-)$ .

4. Je prépare mon tableau de signes.

Je résous $x-1=0\\x=1$

Je résous $x+1=0\\x=-1$

Je place les valeurs $-1$ et $1$ sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.

Je remplis le tableau avec des signes $(-)$ , $(+)$ , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur $x-1$ , comme $a=1$ , on commence par le signe $(-)$ jusqu’au zéro et on complète avec des $(+)$ .

Sur la ligne du facteur $x+1$ , comme $a=1$ , on commence par le signe $(-)$ jusqu’au zéro et on complète avec des $(+)$ .

Pour compléter la ligne du produit $(x-1)(x+1)$ , j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit $(x-1)(x+1)$ est de signe $(-)$ pour la deuxième colonne qui correspond aux valeurs de x comprises entre $-1$ et $1$ .

Je ne prends pas les valeurs $-1$ et $1$ car le produit ne peut pas être nul. Donc j’ouvre les crochets en $-1$ et $1$ , ce qui signifie que les crochets sont tournés vers l’extérieur.

S= ]-1;1[

Donc la courbe est située strictement en dessous de la droite $d$ pour $x \in ]-1;1[$