logo

Exercice de synthèse sur les vecteurs niveau seconde (3)

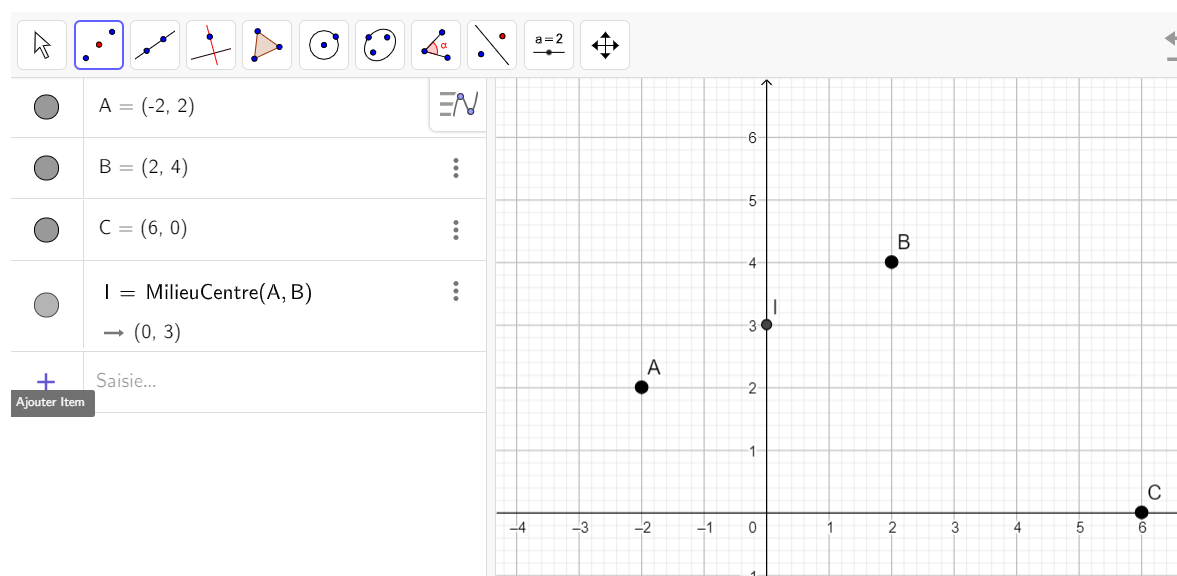
 SoientA(-2;2), B(2;4), C(6;0) trois points du plan.

On note I le milieu du segment [AB].

Le point J est défini par l’égalité vectorielle suivante: \overrightarrow{CJ}=\frac{1}{4}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA}

  1. a. Placer le point I  dans le repère ci-dessus. Puis conjecturer graphiquement ses coordonnées.

Pour placer I, cliquer gauche sur le deuxième onglet en haut à gauche  , sélectionner Milieu ou centre dans le menu déroulant puis cliquer gauche  dans le repère sur le point  A et sur le point B.

Le logiciel le nomme D, cliquer droit sur ce point et sélectionner Renommer dans le menu déroulant puis l’appeler I.

correction
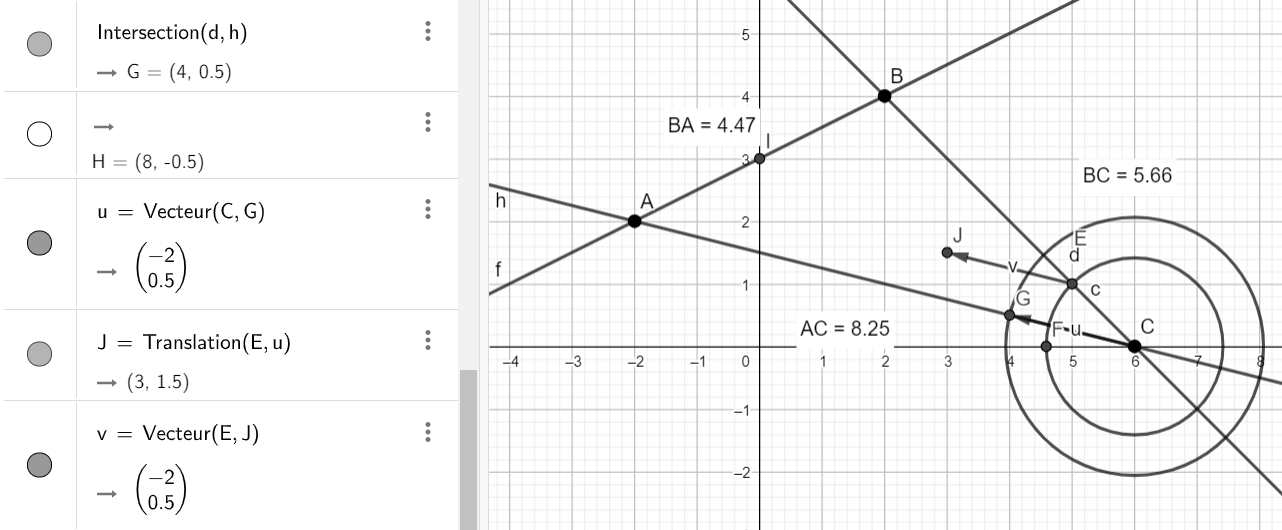
  1. b. Placer le point J dans le repère ci-dessus. Puis conjecturer graphiquement ses coordonnées.

1)A partir de C, je reporte un vecteur égal à \frac{1}{4}\overrightarrow{CB}

Avec Géogébra cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point  C  et sur le point B .

Puis cliquer gauche sur le 8ème onglet en partant de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer gauche sur le point C  et sur le point B . 

Enfin cliquer gauche sur le 6ème onglet en partant de la gauche et sélectionner Cercle ( centre-rayon) dans le menu déroulant.

Dans le repère cliquer gauche sur le point  C  et écrire  CB/4 dans la case Rayon .

Construire le vecteur égal à \frac{1}{4}\overrightarrow{CB}

2) A la suite du vecteur tracé précédemment, je reporte un vecteur égal à \frac{1}{4}\overrightarrow{CA}

a) je construis le vecteur \frac{1}{4}\overrightarrow{CA}

Avec Géogébra cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Droite dans le menu déroulant. Dans le repère cliquer gauche sur le point  C  et sur le point A .

Puis cliquer gauche sur le 8ème onglet en partant de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer gauche sur le point C  et sur le point A . 

Enfin cliquer gauche sur le 6ème onglet en partant de la gauche et sélectionner Cercle ( centre-rayon) dans le menu déroulant.

Dans le repère cliquer gauche sur le point  C  et écrire  CA/4 dans la case Rayon .

Construire le vecteur égal à \frac{1}{4}\overrightarrow{CA}

b) je construis un représentant du vecteur \frac{1}{4}\overrightarrow{CA}

Enfin cliquer gauche sur le 3ème onglet en partant de la gauche et sélectionner Représentant dans le menu déroulant.

Dans le repère cliquer gauche sur l’extrémité du vecteur \frac{1}{4}\overrightarrow{CB}et sur le vecteur \frac{1}{4}\overrightarrow{CA}.

On obtient alors le point J.

correction

2. Calculer les coordonnées du point I

On ne peut pas utiliser le résultat de la question 1.a. pour répondre mais on a déjà une idée du résultat.

correction

3. Calculer les coordonnées du point J

On ne peut pas utiliser le résultat de la question 1.b. pour répondre mais on a déjà une idée du résultat.

correction

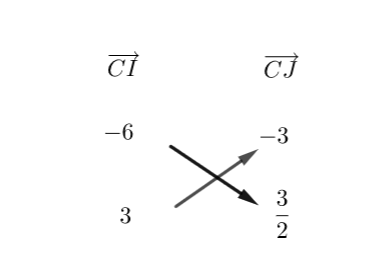
4.a. Calculer les coordonnées du vecteur \overrightarrow{CI}.

Pour conjecturer les coordonnées du vecteur \overrightarrow{CI} à l’aide de Géogébra , cliquer gauche sur le troisième onglet en haut à gauche  , sélectionner Vecteur dans le menu déroulant puis cliquer gauche  dans le repère sur le point  C et sur le point I. Les coordonnées du vecteur \overrightarrow{CI} apparaissent dans la colonne Algèbre.

correction

4.b. Calculer les coordonnées du vecteur \overrightarrow{CJ}.

Pour conjecturer les coordonnées du vecteur \overrightarrow{CJ} à l’aide de Géogébra , cliquer gauche sur le troisième onglet en haut à gauche  , sélectionner Vecteur dans le menu déroulant puis cliquer gauche  dans le repère sur le point  C et sur le point J. Les coordonnées du vecteur \overrightarrow{CJ} apparaissent dans la colonne Algèbre.

correction

4.c. Calculer le déterminant des vecteurs \overrightarrow{CI} et \overrightarrow{CJ}. Qu’en déduire pour les vecteurs \overrightarrow{CI} et \overrightarrow{CJ}? Puis qu’en déduire pour les points C, I et J ?

correction

©2020 – Math’O karé SAS

Les coordonnées du point I sont (0;3).

Dans la colonne Algèbre, on lit J(3;1.5)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-2;2) \hspace{0.4cm} B(2;4)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {(-2)+2}{2}\hspace {2cm}y_I=\frac {2+4}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul ((-2)+2)/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez (-2)+2/2, vous obtiendrez -1 car la machine calculera 2/2 en priorité ce qui est faux

x_I=\frac {0}{2}\hspace {2cm}y_I=\frac {6}{2}

x_I=0\hspace {2cm}y_I=3

Donc I(0;3)

 

On veut déterminer les coordonnées du point J tel que \overrightarrow{CJ}=\frac{1}{4}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA}.

Comme on le les connaît pas, on les appelle x et y. 

On pose  J(x;y).

Les vecteurs \overrightarrow{CJ} et \frac{1}{4}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA} sont égaux donc leurs coordonnées sont égales.

Tâche n°1 : Je calcule les coordonnées de \overrightarrow{CJ} . Puis je calcule les coordonnées de \overrightarrow{CB} et ensuite de \frac{1}{4}\overrightarrow{CB}. Ensuite je calcule les coordonnées de \overrightarrow{CA} et ensuite de \frac{1}{4}\overrightarrow{CA}. Et enfin les coordonnées de \frac{1}{4}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA}

Pour déterminer les coordonnées du vecteur \overrightarrow{CJ}.

Je repère les coordonnées des points C et J.

\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.2cm}x_{J}\hspace{0.2cm}y_{J}

\hspace{1.8cm}C(6;0)\hspace{0.2cm}J(x;y)

J’écris la formule : \overrightarrow{CJ}(x_{J}-x_{C};y_{J}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CJ}(x-6;y-0)

\overrightarrow{CJ}(x-6;y)

Pour déterminer les coordonnées du vecteur \overrightarrow{CB}.

Je repère les coordonnées des points C et B.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}C(6;0)\hspace{0.2cm}B(2;4)

J’écris la formule : \overrightarrow{CB}(x_{B}-x_{C};y_{B}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CB}(2-6;4-0)

\overrightarrow{CB}(-4;4)

Pour obtenir les coordonnées du vecteur \frac{1}{4}\overrightarrow{CB}, je dois multiplier le coordonnées du vecteur \overrightarrow{CB} par \frac{1}{4}.

\frac{1}{4}\overrightarrow{CB}({\frac{1}{4}}\times{(-4)};{\frac{1}{4}}\times{4})\\\frac{1}{4}\overrightarrow{CB}(-1;1)

Pour déterminer les coordonnées du vecteur \frac{1}{4}\overrightarrow{CA}.

Je repère les coordonnées des points C et A.

\hspace{2.1cm}x_{C}\hspace{0.2cm}y_{C}\hspace{0.6cm}x_{A}\hspace{0.2cm}y_{A}

\hspace{1.8cm}C(6;0)\hspace{0.2cm}A(-2;2)

J’écris la formule : \overrightarrow{CA}(x_{A}-x_{C};y_{A}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CA}((-2)-6;2-0)

\overrightarrow{CA}(-8;2)

Pour obtenir les coordonnées du vecteur \frac{1}{4}\overrightarrow{CA}, je dois multiplier le coordonnées du vecteur \overrightarrow{CA} par \frac{1}{4}

\frac{1}{4}\overrightarrow{CA}({\frac{1}{4}}\times{(-8)};{\frac{1}{4}}\times{2})\\\frac{1}{4}\overrightarrow{CA}(-2;\frac{1}{2})

Enfin

\frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB}((-1)+(-2);1+\frac{1}{2})\\\frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB}(-3;\frac{2}{2}+\frac{1}{2})\\\frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB}(-3;\frac{3}{2})

Tâche n°2 : J’écris que les coordonnées de \overrightarrow{CJ}et  de \frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB} sont égales pour obtenir deux équations du premier degré.

L’abscisse de \overrightarrow{CJ}=l’abscisse de \frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB}

x-6=-3

-6 n’est pas à sa place à gauche, j’ajoute 6 de chaque côté.

x=-3+6\\x=3

L’ordonnée de \overrightarrow{CJ}=l’ordonnée de \frac{1}{4}\overrightarrow{CA}+\frac{1}{4}\overrightarrow{CB}

y=\frac{3}{2}

Donc J(3;\frac{3}{2})

 

Pour déterminer les coordonnées du vecteur \overrightarrow{CI}.

Je repère les coordonnées des points C et I.

\hspace{0.5cm}x_{C}\hspace{0.2cm}y_{C}\hspace{1cm}x_{I}\hspace{0.2cm}y_{I}

\hspace{0.3cm}C(6;0)\hspace{1cm}I(0;3)

J’écris la formule : \overrightarrow{CI}(x_{I}-x_{C};y_{I}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CI}(0-6;3-0)

\overrightarrow{CI}(-6;3)

 

Pour déterminer les coordonnées du vecteur \overrightarrow{CJ}.

Je repère les coordonnées des points C et J.

\hspace{0.5cm}x_{C}\hspace{0.2cm}y_{C}\hspace{1cm}x_{J}\hspace{0.2cm}y_{J}

\hspace{0.3cm}C(6;0)\hspace{1cm}J(3;\frac{3}{2})

J’écris la formule : \overrightarrow{CJ}(x_{J}-x_{C};y_{J}-y_{C})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{CJ}(3-6;\frac{3}{2}-0)\\\overrightarrow{CJ}(-3;\frac{3}{2})

Pour calculer le déterminant des vecteurs \overrightarrow{CI} et \overrightarrow{CJ}, on utilise la disposition pratique suivante :

det(\overrightarrow{CI};\overrightarrow{CJ})=-6\times \frac{3}{2}-3\times (-3)\\det(\overrightarrow{CI};\overrightarrow{CJ})=-9+9\\det(\overrightarrow{CI};\overrightarrow{CJ})=0

donc les vecteurs \overrightarrow{CI} et \overrightarrow{CJ} sont colinéaires.

donc les points C , I et  J sont alignés.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.